Bài toán 5: (lấy ví dụ để tham khảo)
Ta biết những điều gì trước những thông tin cho bởi biểu đồ sau:
Đơn vị: nghìn tỉ đồng |
Có thể bạn quan tâm!
-
Tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy môn toán đại số nâng cao 10 - thpt - 9 -
Tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy môn toán đại số nâng cao 10 - thpt - 10 -
Tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy môn toán đại số nâng cao 10 - thpt - 11 -
Phân Phối Thời Lượng . Chữa Các Bài Tập: 37.38,41 -
Tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy môn toán đại số nâng cao 10 - thpt - 14 -
Tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy môn toán đại số nâng cao 10 - thpt - 15
Xem toàn bộ 128 trang tài liệu này.
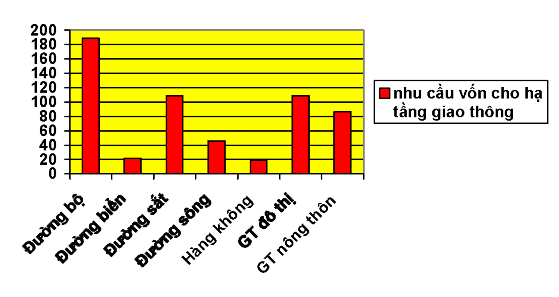
Qua biểu đồ ta thấy nhu cầu vốn cho giao thông đường bộ là 189 nghìn tỉ đồng, cho giao thông đường biển là 21,9 nghìn tỉ đồng vv..
Bài toán 5: Dựa vào biểu đồ hình quạt dưới đây. Hãy lập bảng cơ cấu giá trị sản xuất công nghiệp trong nước năm 2008, phân theo thành phần kinh tế.
(1): Khu vực doanh nghiệp nhà nước (2): khu vực ngoài quốc doanh
(3): Khu vực đầu tư nước ngoài.
khu vực doanh nghiệp nhà nước
khu vực ngoài quốc doanh
khu vực đầu tư nước ngoài
Bảng cơ cấu giá trị sản xuất công nghiệp trong nước năm 2008.
Số phần trăm | |
(1). Khu doanh nghiệp nhà nước (2). Khu doanh nghiệp quốc doanh (3). Khu doanh nghiệp đầu tư nước ngoài | 22,5 33,2 44,3 |
Cộng | 100% |
Bài toán 6: Cơ cấu ( phân hoạch) tập thể HS khối 10 trường THPT A phân theo điểm thi toán ( Cuối năm 2007-2008)
Số phần trăm | |
HS kém (từ 1 điểm đến 2 điểm) HS yếu (từ 3 điểm đến 4 điểm) HS trung bình ( từ 5 điểm đến 6 điểm)ến HS khá (từ 7 điểm đến 8 điểm) HS giỏi ( từ 9 điểm đến 10 điểm) | 7,8% 19% 37,3% 25% 8,9% |
Cộng | 100% |
Hãy vẽ biểu đồ hình quạt mô tả các kí hiệu trên.
Biểu đồ hình quạt mô tả điểm thi môn toán (cuối năm học:2007-2008) (1). HS kém (từ 1 điểm đến 2 điểm)
(2). HS yếu (từ 3 điểm đến 4 điểm)
(3). HS trung bình (từ 5 điểm đến 6 điểm) (4). HS khá ( từ 7 điểm đến 8 điểm)
(5). HS giỏi (từ 9 điểm đến 10 điểm)
Dựng biểu đồ là giáo dục cho HS ý thức tìm hiểu và mô tả sự kiện quan trọng, những hiện tượng muôn màu muôn vẻ trong cuộc sống, từ những kế hoạch văn hoá kinh tế, nông thôn, đất nước con người, khi dạy và học về thông kê có rất nhiều cơ hội để học sinh thực hiện toán học hoá các tình huống, các vần đề trong cuộc sống. Bằng các hoạt động thực tiễn như vậy học sinh sẽ nắm chắc được các vấn đề thống kê cụ thể rõ ràng hơn. Thống kê rất cần thiết cho người lao động nó luôn có ý nghĩa với đời sống con người trong nhiều lĩnh vực của cuộc sống.
Kết luận chung.
Tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy học một số chương đại số nâng cao 10- THPT đã thể hiện được cho HS thấy khả năng ứng dụng toán học vào cuộc sống thực tiễn là một mục tiêu xuyên suốt, một nhiệm vụ quan trọng trong dạy học môn toán ở nhà trường phổ thông. Dạy học môn toán ở nhà trường phổ thông rất cần cho HS vận dụng những tri thức và phương pháp toán học vào những môn học trong nhà trường, ngoài ra còn được vận dụng giải thích các sự việc trong cuộc sống thông qua những hoạt động thực hành toán học trong nhà trường và ngoài nhà trường như nhà máy ngoài ruộng đồngvv… Kể cả những tính chất nghiên cứu bao gồm cả các khâu đặt bài toán, xây dựng mô hình, thu nhập dữ liệu, xử lí mô hình. Để tìm lời giải, đối chiếu với thực tiễn để kiểm tra và điều chỉnh. Việc tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy học môn toán dẫn tới hình thành phẩm chất luôn luôn muốn ứng dụng tri thức và phương pháp toán học để giải thích, phê phán và giải quyết những sự việc xảy ra trong cuộc sống. Vì thế phải luôn coi trọng và cần thiết phải tìm ra những biện pháp tích cực hơn, hiệu quả hơn nữa ngay từ khi HS còn ngồi trên nghế nhà trường, cụ thể ở ngay từ trong các bài mà HS được học cần lồng và tăng cường làm đậm nét hơn nữa mạch ứng dụng toán học và toán học ứng dụng. Qua đó không những HS được củng cố các kiến thức đã học mà quan trọng hơn là hình thành rèn luyện cho HS phát triển năng lực trí tuệ, hình thành khả năng tư duy, suy luận đặc trưng của toán học cần thiết cho cuộc sống tương lai của mỗi người và góp phần cho đất nước thêm phồn vinh.
Chương 3.
Thực nghiệm sư phạm
3.1. Mục đích, nhiệm vụ thực nghiệm
3.1.1. Mục đích.
Xem xét tính khả thi và hiệu quả của việc tăng cường vận dụng các bài toán có nội dung thực tiễn vào dạy học môn toán đại số nâng cao 10- THPT. Qua đó nhằm nắm được phương pháp chung để giải các bài toán có nội dung thực tiễn.
3.1.2. Nhiệm vụ
+ Thiết kế giáo án đã đề ra và tổ chức giờ dạy thực nghiệm tại trường THPT Lương Ngọc Quyến – Thái Nguyên.
+ Kiểm tra và đánh giá Kết quả thử nghiệm thông qua thái độ, khả năng nhận thức của HS.
3.2. Phương pháp thực nghiệm
Trực tiếp dạy mẫu và kiểm tra các lớp 10A10 (cơ bản A), 10A15 (cơ bản D), 10A12(cơ bản C).
3.3. Nội dung và tiến trình thực nghiệm.
3.3.1. Nội dung thực nghiệm
Thiết kế bài dạy và tiến hành dạy trong 4 tiết thể hiện qua Một số bài soạn theo hướng toán học gắn liền với thực tiễn cuộc sống
Soạn bài: Luyện tập Phương trình bậc hai 1 ẩn (tiết 2)
I. Mục tiêu.
1. Kiến thức: Củng cố các kiến thức đã học trong bài 2 về phương trình bậc hai 1ẩn, về phép biến đổi tương đương các phương trình.
2. Kỹ năng: rèn luyện các kỹ năng , giải và biện luận phương trình bậc hai 1 ẩn có chứa tham số .
3. Thái độ: Rèn luyện tính cẩn thận, óc tư duy lôgíc và tổ hợp.
II. Chuẩn bị của giáo viên và học sinh.
Giáo viên: Chuẩn bị các kiến thức HS đã được học từ lớp 9 để đặt câu hỏi, chuẩn bị hình vẽ và phấn màu,..
Học sinh: Chuẩn bị bài tập ở nhà, đến lớp cùng với GV chữa bài tập trọng
tâm từ 16 đến bài 21. Ôn lại kiến thức đã học và ôn lại phần chương trình năm học lớp 9 về phương trình bậc hai 1 ẩn.
Phương pháp dạy học. gợi ý trả lời các câu hỏi và bài tập
III. Tiến trình dạy học.
A. Gợi động cơ
Các bài tập về PT bậc nhất và bậc hai 1 ẩn số rất đa dạng và phong phú, có tác dụng cho các em phát triển được năng lực giải toán và khả năng tư duy sáng tạo. Theo phân phối chương trình có hai tiết luyện tập, ở giờ trước ta đã luyện tập được một tiết, hôm nay ta sẽ cùng nhau luyện tập tiết thứ hai về vấn đề phương trình bậc hai chứa tham số ngoài việc ứng dụng trong nội bộ môn toán nó còn được ứng dụng rất nhiều trong thực tiễn cuộc sống của chúng ta.
B.Kiểm tra bài cũ:
Câu hỏi 1: Nêu cách giải và biện luận phương trình bậc hai 1 ẩn số.
C. bài mới.
Hoạt Động 1
Bài tập 1: Tìm m để phương trình có nghiệm. 15x2 -2mx+6400-m2 =0 (1)
Hoạt động của HS | |
Câu hỏi 1 (1) có phải là PT bậc hai không ? Câu hỏi 2 Một phương trình bậc 2 có nghiệm khi nào? | Gợi ý trả lời câu hỏi1. (1) là phương trình bậc 2 vì hệ số x2 là 15 , khác 0 Gợi ý trả câu hỏi 2 Khi b2 4ac 0 Hoặc 2 ' b' ac 0 |
Đáp số đúng của bài toán là: ' m2 6000 Phương trình có nghiệm khi ' 0 m2 600haym 600 m 600 |
Hoạt động 2:
M2
Bài tập 2:Có hai nhà máy M1 và M2. Nhà máy M2 nằm cách đoạn đường sắt theo đường thẳng là 20km. Hỏi phải đặt ga xép A ở vị trí nơi nào để từ nhà máy M1 đến nhà máy M2 theo đường sắt M1A (đoạn đường sắt chỉ đến vị trí A) và đường bộ AM2 mất ít thời gian nhất/? Biết rằng vận tốc của tàu hoả là 48km/h và vận tốc của các phương tiện đường bộ chỉ là 12km/h.
hoạt động của HS | |
Giáo viên hướng dẫn HS vẽ sơ đồ của bài toán ở vị trí 2 nhà máy và quãng đường tàu hoả và đường bộ. Câu hỏi 1: Để biết khoảng thời gian đi từ nhà máy M1 đến nhà máy M2 ta hải biết yếu tố nào? Câu hỏi 2: Muốn biét thời gian từ M1 đến A thì phải biết điều gì khi biết vận tốc tàu hoả 48km/h? Câu hỏi 3: Nếu gọi khoảng cách M1B là a và khoảng cách AB là x khi đó | M2 M1 Gợi ý trả lời câu hỏi 1 Ta cần biết thời gian đoạn đường sắt từ M1 đến A và doạn đường bộ từ A đến M2. Gợi ý trả lời câu hỏi 2. Phải tìm khoảng cách M1A Gợi ý trả lời câu hỏi 3 |
Để tính M1A và AM2 theo a,x Ta có: M1A=a-x Và AM2 = AB2 M B2 x2 202 2 Gợi ý trả lời câu hỏi 3. Thời gian tàu hoả đi hết đoạn M1A là: M1 A a x 48 48 Thời gian để :đi hết đoạn đường bộ AM2là 2 2 AM 2 x 20 12 12 Gợi ý trả lời câu hỏi 4. Thời gian để đi từ M1 đến M2 là:t= a x x2 400 (1)Từ (1) ta có PT: -x+ 48 12 x2 400 =48t-a Đặt m= 48t-a thay vào trên ta có : -x + 4 x2 400 = m 4 x2 400 = m+x 15x2 -2mx + 6400 –m2 =0 Gợi ý trả lời câu hỏi 6 m Gợi ý trả lời câu 7,8 Như kết quả bài 1 vì thời gian t>0, m= 48t –a nên t nhỏ nhất khi m nhỏ nhất.Từ điều kiện có nghiệm của PT ta tìm được giá trị nhỏ nhất của m là m= 600 và khi đó tìm được x 5,16. |
Hoạt động 3:
Bài tập 3:
Có hai đường sắt cắt nhau theo một góc vuông. Hai ga I và II tương ứng trên hai đường sắt đó. Cách điểm giao nhau của hai đường sắt là 40km và 50km. Hai chuyến tàu khởi hành cùng một lúc từ hai ga trên và cùng đi về phía cắt nhau của hai đường sắt. Tàu I có vận tốc 800m/phút, tàu II có vận tốc 600m/phút. Để đảm bảo an toàn, khoảng cách tối thiểu của hai con tàu là 100m. Hỏi hai chuyến tàu vận hành như trên có đảm bảo an toàn không?
Hoạt động của HS | |
GV hướng dẫn HS vẽ sơ đồ chuyển động của hai con tàu. Câu hỏi 1: Để biết hai con tàu có an toàn không ta cần biết cái gì? Câu hỏi 2:Giả sử đặt khoảng cách đó là m,ta cần có thêm đại lượng nào nữa để có thể tính được m? Câu hỏi 3:Giả sử sau x phút hai con tàu con tàu có khoảng cách bé nhất là m= MN.Hãy tính BM và OM? Câu hỏi 4: Tương tự hãy tính ON? Câu hỏi 5: Hãy biểu diễn m qua x? Câu hỏi 6:Tìm m để PT trên có nghiệm? Câuhỏi 7: Tại sao không lấy giá trị m 16 Câu hỏi 8: Khoảng cách bé nhất giữa | B 50 km M 40km A N O Gợi ý trả lời câu 1 Ta cần biết khoảng cách bé nhất của hai con tàu có thể đạt được trên lộ trình của chúng. Gợi ý trả lời câu 2 Ta cần biết thêm về thời gian mà hai con tàu có được khoảng cách m đó. |