Sức bền vật liệu - 10

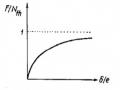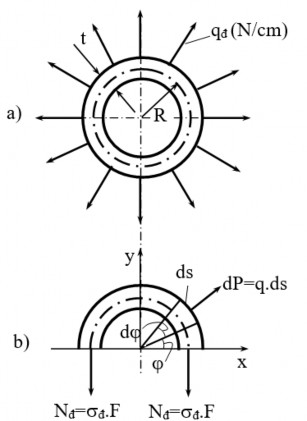
Hình 4.2: Bài toán chuyển động quay với vận tốc góc không đổi

Lập tổng hình chiếu các lực theo phương y, ta được:

x FR2 x FR2

2.N®q®.ds.sin d.sin d2 .

2 2

0 g0



Có thể bạn quan tâm!

• Khái Niệm, Phương Trình Vi Phân Của Đường Đàn Hồi
• Quan Hệ Độ Vòng - Lực Nén (Dạng Không Thứ Nguyên)
• Bài Toán Kéo Vật Nặng Lên Cao Với Gia Tốc Không Đổi
• Sức bền vật liệu - 11

Xem toàn bộ 91 trang tài liệu này.

g

.2 .R2

Ứng suất kéo

đ trong vô lăng là: đ g

Nhận xét: ứng suất trong vô lăng đ tăng rất nhanh nếu tăng  hay R.

Ðiều kiện bền khi tính vô lăng là:

.2 .R2

đ g

k

trong đó []k: ứng suất cho phép khi kéo của vật liệu

Ghi chú :Chu kỳ T là khoảng thời gian thực hiện một dao động (s). Tần số f là số dao động trong 1 giây (hertz). Tần số vòng (tần số riêng): số dao động trong 2

giây:

2 2f T

Ví dụ 4.1:

Cho dầm bê tông dài 5m, có trọng lượng riêng = 22k N/m3 được kéo lên cao

nhanh dần đều, sau 10s đưa lên cao được 10m so với vị trí nằm yên ban đầu. Diện tích tiết diện A=600 cm2. Bỏ qua trọng lượng dây, xác định lực kéo trong dây và mô men uốn lớn nhất trong dầm. (Hình 4.3)

Bài giải:

Gia tốc chuyển động nhanh dần đều xác định theo công thức:

a 2 S v t 2 .10  0, 2m / s2

t2 0102

Gia tốc hướng lên, cùng chiều chuyển động. Khối lượng của dầm phân bố đều nên lực quán tính là một hệ lực phân bố đều hướng xuống với cường độ:

aqt

ma A a

g

Đặt hệ lực quán tính vào dầm, hệ được xem là ở trạng thái tĩnh. Dầm chịu lực phân bố đều gồm trọng lượng riêng và lực quán tính với cường độ tổng cộng là:

q q q

A A a 

a 

0, 2  1,3469kN / m

bt qt

g A1 g 

22.0, 61

9,81



Lực căng trong dây:

N qL  1,3469.2,5  3,3673kN

2

Giá trị lớn nhất của biểu đồ mô men uốn:

Mm q

0, 2071L2

2

 1,3469

0, 2071L2 2

 0, 7219kN / m

N

N

0,2071L

0,5858L

0,2071L

bt qt

q= q + q

Mm

Mm

M m

(M)

Hình 4.3: Bài toán nâng dầm lên nhanh dần đều

4.3. BÀI TOÁN CÓ GIA TỐC THAY ĐỔI THEO THỜI GIAN

4.3.1. Bậc tự do của hệ

P

y

x

a) b) P

y

P1 P2

y

y

1 2

Hình 4.4: Xác định bậc tự do của hệ

Khi chuyển động, các phần vật chất của hệ sẽ chuyển động. Số lượng các thông số độc lập cần thiết đủ để xác định vị trí tất cả các khối lượng trên hệ được gọi là số bậc tự do. Trên hình 4.4a, dầm không khối lượng mang một vật nặng P, để xác định vị trí của vật nặng P ta chỉ cần biết độ vòng y tại tiết diện đặt vật nên hệ có một bậc tự do. Trên hình 4.4b là dầm mang hai khối lượng, hệ có hai bậc tự do. Trên hình 4.4c tuy hệ mang một vật nặng nhưng cần hai thông số mới xác định đầy đủ vị trí của vật ở trạng thái biến dạng, hệ có hai bậc tự do.

Ở phần tiếp theo, ta chỉ khảo sát hệ có một bậc tự do.

4.3.2. Phương trình vi phân tổng quát của hệ một bậc tự do

Xét dầm mang khối lượng m (bỏ qua trọng lượng bản thân dầm) và chịu lực

F(t) thay đổi theo thời gian tại tiết diện đặt khối lượng như sơ đồ trên hình 4.5

y0

y(t)

2

F(t) 1

Hình 4.5: Sơ đồ bài toán dao động của hệ một bậc tự do.

Ta gọi trạng thái cân bằng ban đầu là trạng thái của dầm chỉ chịu khối lượng m, khối lượng này có chuyển vị y0. Hệ là đàn hồi tuyến tính nên quan hệ giữa lực tác động và chuyển vị là:

y0 .mg

(4.5)

Có thể thấy là chuyển vị tại tiết diện đặt khối lượng do lực bằng đơn vị đặt tại tiết diện đó gây ra. Giá trị y0 hoặc có thể tìm thấy bằn các phương pháp đã biết.

Sau khi chịu lực động F(t), còn gọi là lực cưỡng bức, khối lượng m sẽ có chuyển vị thêm y(t) tính từ trạng thái cân bằng ban đầu.

Đặt vào dầm lực quán tính F qt ma my&&(t) , dầm sẽ ở trạng thái tĩnh và ta có

thể tìm được chuyển vị thêm y(t). Các lực gây ra chuyển vị thêm gồm lực động F(t), lực quán tính Fqt và để tổng quát ta xét cả lực cản nhớt, là loại lực cản ngược chiều

chuyển động và tỷ lệ với vận tốc F c y&, β gọi là hệ số tỷ lệ.

Lực cản nhớt nói chung bao gồm các lực cản của môi trường, lực cản do ma sát của các liên kết và lực cản bên trong của bản thân kết cấu.

Hệ ở trạng thái tĩnh nên ta vẫn có quan hệ giữa lực và chuyển vị theo (4.3):

ytFtFqt FcFtm&y&ty&t

Quan hệ này được viết gọn dưới dạng

&y&t 2y&t2ytFt

m

(4.6)

Trong đó ta đặt:

2

m

(4.7)

2 1

m

(4.8)

α < .

tự do.

Trong đó α gọi là hệ số cản nhớt, xác định bằng thực nghiệm, và ta thường gặp Quan hệ (4.4) là phương trình vi phân chuyển động tổng quát của hệ có một bậc

4.4. BÀI TOÁN DAO ĐỘNG TỰ DO

4.4.1. Khái niệm chung về dao động

Khi nghiên cứu về dao động của hệ đàn hồi, trước tiên ta cần có khái niệm về bậc tự do: bậc tự do của một hệ đàn hồi khi dao động là số thông số độc lập để xác định vị trí của hệ.

Ví dụ: hình 4.6a, nếu bỏ qua trọng lượng của dầm thì hệ có 1 bậc tự do (chỉ cần biết tung độ y của khối lượng m xác định vị trí của vật m). Nếu kể đến trọng lượng của dầm thì hệ có vô số bậc tự do vì cần biết vô số tung độ y để xác định mọi điểm trên dầm.

Trục truyền mang hai puli (hình 4.6b). Nếu bỏ qua trọng lượng của trục thì hệ có 2 bậc tự do (chỉ cần biết hai góc xoắn của hai puli ta sẽ xác định vị trí của hệ).

Khi tính phải chọn sơ đồ tính, dựa vào mức độ gần đúng cho phép giữa sơ đồ tính và hệ thực đang xét.

Ví dụ: nếu khối lượng m rất lớn so với khối lượng của dầm phải lập sơ đồ tính là khối lượng m đặt trên dầm đàn hồi không có khối lượng nên hệ có một bậc tự do. Nếu trọng lượng của khối lượng m không lớn so với trọng lượng dầm, ta phải lấy sơ đồ tính là một hệ có vô số bậc tự do và bậc tự do của một hệ xác định theo sơ đồ tính đã chọn, nghĩa là phụ thuộc vào sự gần đúng mà ta đã chọn khi lập sơ đồ tính.

Dao động của hệ đàn hồi được chia ra:

Dao động cưỡng bức: dao động của hệ đàn hồi dưới tác dụng của ngoại lực biến đổi theo thời gian (lực kích thích).

P(t)  0

Dao động tự do: dao động không có lực kích thích P(t)=0:

Dao động tự do không có lực cản: hệ số cản 

 = 0; P(t) = 0

Dao động tự do có để ý đến lực cản của môi trường:  0 ; P(t) = 0

Trọng lượng của khối lượng m được cân bằng với lực đàn hồi của dầm tác động lên khối lượng.

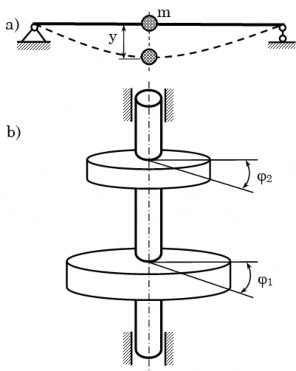
Hình 4.6: Dao động của hệ đàn hồi một bậc và nhiều bậc tự do

4.4.2. Dao động của hệ đàn hồi một bậc tự do

a) Phương trình vi phân biểu diễn dao động

Dầm mang khối lượng m (bỏ qua trọng lượng dầm). Lực kích thích P(t) biến đổi theo thời gian tác dụng tại mặt cắt ngang có hoành độ z. Tìm chuyển vị y(t) của khối lượng m theo thời gian t.

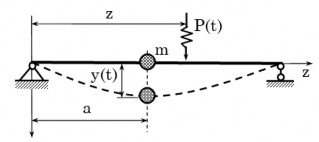
Hình 4.7: Dao động hệ một bậc tự do

Vận tốc và gia tốc của khối lượng này là:

dy d2 y

v  y&(t) 

; a  &y&(t) 

dt dt2

Chuyển vị của m do những lực sau đây gây ra: Lực kích thích P(t), lực cản ngược chiều chuyển động và tỷ lệ với vận tốc:

Fc= -y&; ( - hệ số cản), lực quán tính: Fqt = - m &y&

Gọi  là chuyển vị gây ra do lực bằng một đơn vị tại vị trí m  chuyển vị do lực P(t) gây ra là .P(t), chuyển vị do lực cản gây ra là .Fc= - .y&(t) , chuyển vị do lực quán tính gây ra là -.m &y&(t)

Chuyển vị do các lực tác dụng vào hệ gây ra là

y(t) P(t) y&(t) m&y&(t)

(4.9)

Chia (4.9) cho m. và đặt: 2 ;

m

2 

1

m.

Do đó ta có :

&y&(t) 2y&(t) 2y(t) P(t)

m

(4.10)

 Ðây là phương trình vi phân của dao động. Hệ số  biểu diễn ảnh hưởng của lực cản của mối trường đến dao động và  < .

b) Dao động tự do không có lực cản

Dao động tự do không có lực cản: P(t) = 0,  = 0.

Phương trình vi phân của dao động có dạng:

&y&(t) 2y(t) 0 (4.11)

Nghiệm của phương trình này có dạng: y(t) = C1cost + C2sint

Biểu diễn C1 và C2 qua hai hằng số tích phân mới là A và  bằng cách đặt: C1 = A sin ; C2 = A cos

Ta có phương trình dao động tự do: y(t) = A sin(t + ) (4.12)

Điều kiện ban đầu t = 0 => y(0) = y0; Phương trình (4.12) cho thấy:

y&(0)  y&0

xác định C1 và C2

 Chuyển động tự do không lực cản là một dao động điều hoà có biên độ A và

chu kỳ T = 2. Đồ thị dao động hình sin như trên hình 4.8.



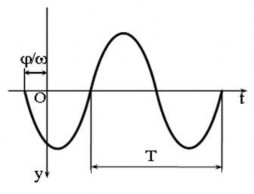
Hình 4.8: Đồ thị dao động tự do không cản

 Tần số dao động f =1.

T 2

g

y0

 Tần số góc hay tần số dao động riêng:  = 2f ;

1

m

g mg



(Hert = 1/s)

c) Dao động tự do có kể đến lực cản

Vì P(t) = 0,  0, khi đó phương trình vi phân của dao động là:

&y&(t) 2y&(t) 2y(t) 0 (4.13)

Với điều kiện hạn chế  <  (lực cản không quá lớn), nghiệm có dạng:

y(t)  Aet sin( t )

1

Dao động là hàm tắt dần theo thời gian với tần số góc:

(4.14)

1 

Chu kỳ dao động:



2 2

2



1

12

2

2



T1 

1

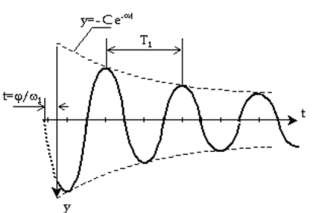
Hình 4.9:Đồ thị dao động tự do có cản

Dạng dao động được biểu diễn trên hình 4.9, biên độ dao động giảm dần theo thời gian, bởi vậy ta gọi là dao động tự do tắt dần. Khi lực cản càng lớn, tức là hệ số  càng lớn thì sự tắt dần càng nhanh.

Sau mỗi chu kỳ T1, biên độ dao động giảm với tỉ số:

Tức là giảm theo cấp số nhân

4.5. BÀI TOÁN VA CHẠM

et e(tT1)

 eT1

 const

4.5.1. Va chạm theo phương thẳng đứng

Xét một dầm, bỏ qua trọng lượng bản thân, mang vật nặng P và chịu va chạm bởi vật nặng Q rơi theo phương thẳng đứng vào dầm tại tiết diện đặt vật nặng P với

Q

P

yt yd

a)

b)



Q

c)

yt

Hình 4.10: Va chạm thẳng đứng trên hệ một bậc tự do

vận tốc lúc va chạm v0 như trên hình vẽ 4.10.

Ở trạng thái ban đầu, khi chưa va chạm, do trọng lượng P tiết diện đặt vật có chuyển vị y0.

Sau va chạm, ta giả thiết cả hai vật P, Q cùng chuyển động xuống dưới, đạt

chuyển vị lớn nhất yd rồi sau đó thực hiện dao động tự do tắt dần quanh vị trí cân bằng ban đầu.

Gọi trạng thái 1 là trạng thái khi vật Q chạm vật P và cả hai cùng di chuyển xuống dưới với vận tốc v1. Trạng thái 2 là trạng thái khi vật Q và P đạt tới chuyển vị lớn nhất yd xuống phía dưới.

Áp dụng nguyên lý bảo toàn năng lượng cho quá trình hệ chuyển từ trạng thái 1

sang trạng thái 2

K U T