Sức bền vật liệu - 11

m v2 m v2

Biến thiên của động năng:

K K2 K1 2 21 1, với v2 = 0.

2 2

Theo định lý bảo toàn động lượng thì động lượng trước khi va chạm, là Q v sẽ

g0

bằng động lượng sau va chạm, là: Q P v .Ta có:

g 1

Q v Q P v v Q v

Có thể bạn quan tâm!

• Quan Hệ Độ Vòng - Lực Nén (Dạng Không Thứ Nguyên)
• Bài Toán Kéo Vật Nặng Lên Cao Với Gia Tốc Không Đổi
• Sức bền vật liệu - 10

Xem toàn bộ 91 trang tài liệu này.

g0

Vậy:

g 1 1

Q P 0

K 

Q P Q

v Q v2

2g Q P 0 2g Q P0

2

2



Thế năng biến dạng đàn hồi của hệ được tính trên cơ sở đồ thị quan hệ tuyến tính giữa lực – chuyển vị như trên hình (4.5), biểu đồ này đúng khi thanh chịu tải trọng tĩnh cũng như khi thanh chịu tải trọng động theo các giả thiết đã nêu.

Löïc

P

y0Chuyeån vò

Hình 4.11: Đồ thị tính thế năng biến dạng

Ở trạng thái 1, do lực tĩnh P thanh có chuyển vị y0, thế năng biến dạng đàn hồi tương ứng:

U Py0 12

Sử dụng ký hiệu chuyển vị đơn vị là , chuyển vị do một lực có trị số bằng 1

đặt theo phương va chạm gây ra như trên hình (4.4b), ta có thể viết:

y2

y P U 0

0 1 2

d 0 d

Ở trạng thái 2, thanh có chuyển vị (y0+yd). Do giả thiết tính chất vật liệu khi tải trọng tĩnh cũng như khi tải chịu tải trọng động, ta có thể viết biểu thức tương tự như của thế năng biến dạng đàn hồi:

U y0

yd ;

U U

y2  2 y y

2

2 2

2 1 2

U

Công của ngoại lực trong di chuyển từ trạng thái 1 tới trạng thái 2 là công của

các trọng lượng Q + P không đổi trong đoạn chuyển dời yd. Vậy:

TQP.yd

Từ nguyên lý bảo toàn năng lượng K U T , ta có:

Q2

2

y  2 y y

v2 d 0 dQ Py

2g Q P0 2d

Hay:

y2  2 y y  2Q Py

Qv2

(4.15)

d 0 d d

P 0

Lượng P y0

g 1

Q



là chuyển vị theo phương va chạm của tiết diện va chạm do một

lực bằng trọng lượng P đặt tĩnh theo phương va chạm gây ra.

Lượng Q , ký hiệu yt, là chuyển vị theo phương va chạm của tiết diện va chạm do một lực bằng trọng lượng P và đặt tĩnh theo phương va chạm gây ra, sơ đồ xác định yt như trên hình 4.10c.

Phương trình (4.15) được viết gọn dưới dạng như sau:

2 v2

yd  2 yt yd 0yt  0

(4.16)

P 

Q

g 1



Nghiệm dương của phương trình là:



v2 

y 1 10y

k y

(4.17)

d P 

t d t



t Q

gy 1



10

v2

gy 1P 

t Q 





Trong đó, hệ số động của bài toán va chạm theo phương thẳng đứng là:

kd  1

(4.18)

2gH

1

2H

y 1P 

t Q 





Trường hợp đặc biệt, khi vật nặng Q rơi từ độ cao H xuống dầm, v0 

kd  1

(4.19)

Khi H=0 thì kd = 2, nghĩa là khi đặt đột ngột toàn bộ trị số tải trọng lên hệ thì nội lực,biến dạng, chuyển vị sẽ lớn gấp đôi trường hợp đặt tải tĩnh.

Ví dụ 4.2

Xác định ứng suất pháp lớn nhất trên tiết diện một cột chịu va chạm theo phương thẳng đứng cho trên hình 4.12. Bỏ qua trọng lượng cột.

Cho biết: Q = 600 kN; H = 6 cm; E = 103 kN/cm2.

Bài giải

Chuyển vị tĩnh yt bằng biến dạng dài của cột do trọng lượng Q đặt tĩnh trên cột là:

10cm

Q

1

80cm

F =30cm2

60cm

F2=30cm2

Hình 4.12

y L Q.l1 Q.l2 0, 6.80 0, 6.60  3, 4.103 cm.

t

1 2H

yt

1

2.6

3,4.103

Hệ số động:

EF1 EF2

103.30 103.20

kd  1

 1

 1

 60,41

1

2H

y (1P )

t

Q

Ứng suất pháp lớn nhất trên tiết diện:

kdt

kd

Q 60,41. 0,6  1,82 kN / cm2

A220

4.5.2. Va chạm theo phương nằm ngang

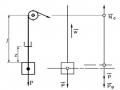
Xét hệ có một bậc tự do chịu va chạm bởi vật nặng Q chuyển động theo phương ngang với vận tốc v0 vào trọng lượng đặt sẵn P (hình 4.13a).

Ở trạng thái ban đầu, khi chưa va chạm, tiết diện đặt tại vật P không có chuyển

vị theo phương ngang. Sau va chạm, ta giả thiết cả hai vật P, Q cùng chuyển động sang phải đạt chuyển vị lớn nhất yd rồi sau đó thực hiện dao động tự do tắt dần quanh vị trí cân bằng ban đầu.

Tiến hành những bước tương tự như đối với trường hợp va chạm theo phương thẳng đứng, ta sẽ tìm được chuyển vị yd. Trong trường hợp đang xét:

v Q v ;

1 Q P 0

Q2 2

K v

2g Q P0

U1  0

( dầm chưa có chuyển vị ngang theo phương va chạm)

y

2

Ud

2 2

Q

( ở trạng thái 2 dầm có chuyển vị yd)

v0

a) b) c) yt

P

1

1

Q

Q

Hình 4.13: Va chạm theo phương ngang

Công ngoại lực T=0 (chuyển vị theo phương vuông góc với trọng lượng Q

và P).

Áp dụng nguyên lý bảo toàn năng lượng K U T , ta có:

y2

d

2

Q2

2g Q P

v2  0

0

Đặt:

yt .Q

: Chuyển vị theo phương ngang do một lực bằng trọng lượng

của vật gây va chạm Q đặt tĩnh theo phương va chạm, xác định theo sơ đồ hình 4.9c.

- Chuyển vị do một lực có trị số bằng 1 đặt theo phương va chạm, xác định theo sơ đồ trên hình 4.9b.

Nghiệm dương của phương trình:

gy 1P 

t Q 





y v0 y k y

(4.20)

d t d t

Hệ số động của bài toán va chạm theo phương ngang là:

gy 1P 

t Q 





v

kd 0

(4.21)

Ví dụ 4.3

Xác định hệ số động của dầm thép chữ I N014 ( Hình 4.14) chịu va chạm bởi vật có trọng lượng 100 N chuyển động theo phương ngang với vận tốc v0 = 20 km/h khi không kể và khi có kể đến trọng lượng của dầm.

Bài giải:

Từ bảng thép định hình, với I N014 ta có các đặc trưng:

- Trọng lượng trên 1 mét dài 137N;

- Mômen quán tính Ix = 572 cm4;

- Môđun đàn hồi E = 2,1.104 kN/cm2

- Chiều dài dầm: l=400 cm

Q

l/2

Q

v0

l/2

l

yt

Hình 4.14

Chuyển vị tĩnh:

Q.l 3



x

yt 48EI

0,1.4003 2



48.2,1.104.572 1,1.10 cm

Vận tốc chuyển động: v0 = 20 km/h = 555,5 cm/s. Khi không kể đến trọng lượng bản thân của dầm

gyt

v

kd 0 

555,5

 169

980.1,1.102

Khi kể đến trọng lượng bản thân của dầm, ta thu gọn trọng lượng về tiết diện va chạm ở chĩnh giữa dầm với hệ số thu gọn là 17/35 và có trọng lượng thu gọn là:

P 17 .137.4  266 N

35

gy (1 P )

t

Q

v

kd 0 

555,5

 88

980.1,1.102 (1 266)

100

Như thế, trọng lượng bản thân làm giảm ảnh hưởng va chạm. Việc không kể trọng lượng bản thân khiến phép tính thiên về an toàn.

4.5.3. Kết luận chung về bài toán va chạm

1. Công thức tính các đại lượng: Trên cơ sở biểu thức tính chuyển vị toàn phần

y y0 yd y0 kd yt

Và quan hệ định luật Hooke, ta có thể viết biểu thức tính đại lượng S bất kỳ trong bài toán va chạm:

Trong đó:

S S0 Sd S0 kd St

S0 - đại lượng cần tính do vật nặng đặt sẵn trên hệ gây ra;

St - đại lượng cần tính do một lực bằng trọng lượng vật gây va chạm Q đặt theo phương va chạm gây ra;

Kd - hệ số động của bài toán va chạm, tính theo (4.18) khi va chạm theo phương thẳng đứng và tính theo (4.21) khi va chạm theo phương nằm ngang.

Trong cả hai trường hợp yt là chuyển vị tĩnh theo phương va chạm do một lực bằng trọng lượng của vật gây va chạm Q đặt tĩnh theo phương va chạm gây ra như đã chỉ trên hình 4.10c hoặc 4.13c.

2. Trường hợp kể tới khối lượng của kết cấu: khi này có thể thu gọn khối lượng về tiết diện chịu va chạm bằng cách sử dụng các hệ số thu gọn khối lượng.

3. Giảm ảnh hưởng của va chạm: Ta giảm hệ số động bằng cách:

- Tăng thêm khối lượng đặt sẵn P. Biện pháp này làm tăng trị số của S0

- Làm mềm kết cấu để tăng thêm trị số chuyển vị yt. Biện pháp này có thể đạt được khi đặt thêm các tấm đệm, lò xo ở tiết diện va chạm hoặc ở các gối tựa.

CÂU HỎI ÔN TẬP CHƯƠNG 4

1. Tại sao ta có thể nói: việc phân loại tải trọng tĩnh và tải trọng động chỉ mang tính ước lệ.

2. Nêu và giải thích các giả thiết về vật liệu khi tính thanh chịu tải trọng động.

3. Ta dùng nguyên lý nào để đưa bài toán động về bài toán tĩnh tương đương khi biết gia tốc của chuyển động.

4. Giải thích những lực tác động lên khối lượng m trong bài toán dao động hệ một bậc tự do.

5. Thế nào là lực cản nhớt. Giải thích nguyên nhân của lực cản nhớt.

1. Nêu các giả thiết khi tính thanh chịu tải trọng va chạm theo SBVL

3. Giải thích các biện pháp làm giảm ảnh hưởng của tải trọng va chạm lên một hệ kết cấu.

4. Giải thích vì sao tính toán va chạm không kể đến khối lượng kết cấu sẽ thiên về an toàn hơn so với tính toán có kể đến khối lượng kết cấu.

9. Một vật nặng trọng lượng Q = 300 N rơi tự do từ độ cao h = 1m xuống một đĩa cứng gắn ở đầu một thanh thép tròn đường kính d = 2cm, chiều dài l=3m. (hình 4.15)

Tính độ dãn dài và ứng suất trong thanh. Bỏ qua trọng lượng của thanh. E = 103 kN/cm2

10. Một vật nặng có trọng lượng Q = 100kN rơi tự do từ độ cao h = 2m xuống va chạm vào dầm AB có chiều dài 4m, mặt cắt ngang tròn đường kính 30cm, vật liệu dầm bằng thép có E = 2.105 MN/m2. Bỏ qua trọng lượng của dầm. (hình 4.16)

Tính độ dịch chuyển theo phương thẳng đứng của mặt cắt C khi va chạm.

11. Một vật nặng trọng lượng Q = 300 N chuyển

Hình 4.15

Q

A

C

B

2 m

2 m

h

Hình 4.16

động đều với vận tốc v = 8,94 m/s đến va chạm vào một đĩa cứng gắn ở đầu một thanh

l

Q v

Hình 4.17

thép tròn đường kính d = 2cm, chiều dài l=3m.(hình 4.17)

Tính độ dãn dài và ứng suất trong thanh. Bỏ qua trọng lượng của thanh. E = 103 kN/cm2.

12. Một dầm cầu trục dài 5m ghép bằng hai thanh thép chữ I số 30 (hình 4.18). Tời B đặt chính giữa dầm có trọng lượng 20kN và nâng một vật có trọng lượng P = 60kN.

Xác định lực căng trong dây cáp của tời và ứng suất pháp lớn nhất trong dầm. Biết P được nâng lên với gia tốc không đổi và sau giây thứ nhất nó đi được 2,5m.

B

2,5m

2,5m

P

Hình 4.18