Bài Toán Kéo Vật Nặng Lên Cao Với Gia Tốc Không Đổi

a) Thanh bằng gang mặt cắt tròn:

i x 

Ix R A 2

l 0, 7.3.2  105

x

i 4.102

Độ mảnh giới hạn 0 của gang xám:

0 

Có thể bạn quan tâm!

• Diện Tích Và Hoành Độ Trọng Tâm Của Một Số Hình Phẳng
• Khái Niệm, Phương Trình Vi Phân Của Đường Đàn Hồi
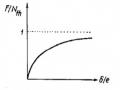
• Quan Hệ Độ Vòng - Lực Nén (Dạng Không Thứ Nguyên)
• Sức bền vật liệu - 10
• Sức bền vật liệu - 11

Xem toàn bộ 91 trang tài liệu này.

 3,14  80

E

tl

11, 5.104

178

Vì  > 0, ta sử dụng công thức Euler để xác định lực tới hạn:

Nth th A 

2 E

2

R2

 3,14.11,5.10442.104

1052

 516.103

MN  516kN

b) Thanh bằng đuyra, mặt cắt ngang hình vành khăn:

Ix

A

R

2

12

i x 

Trong đó:

r 2

R 3

l

ix

0, 7.3

3.102 2 2

 188

3

1

2 

Độ mảnh giới hạn 0 của đuyra:

E

tl

0 

 3,14  62, 3

7,1.104

180

Vì  > 0, ta sử dụng công thức Euler để xác định lực tới hạn:

2 2 

3,14.7,1.104.32.104 1

Nth th A 

2 E

2

R2 12 



1882

3 

 81.103 MN  81kN

a 3

6

c) Thanh bằng gỗ, mặt cắt ngang hình vuông:

i x  0, 29a

l

ix

0, 7.3

0, 29.15.102

 48,3

Độ mảnh giới hạn 0 của gỗ:

0 

 3,14  76

E

tl

104

17

Vì  < 0, ta sử dụng công thức Ianxinxky th a b

trong đó a=29,3 MN/m2; b=0,194 MN/m2:

2

th  29,3  0,194.48,3  19,9MN / m

Lực tới hạn:

4

Nth th A  19.9.10  0, 4478MN  447,8kN

Ví dụ 3.3

để xác định lực tới hạn,

Chọn số hiệu thép chữ I cho thanh dài 2 m, liên kết khớp tại hai đầu và chịu một

lực nén

N 230kN . Biết vật liệu là thép số 2 có 

140MN / m2 .

n

Bài giải

Đây là bài toán chọn tiết diện mặt cắt - vì có hai ẩn là  và A nên ta chọn theo phương pháp đúng dần

a) Lần 1: Chọn = 0,5

Ta có diện tích A là:

A N

n

.

230.103



32,8.10

0,5.140

4 m2

Tra bảng thép định hình chữ I ta chọn số hiệu thép 22a có: A = 32,4 cm2, iy = imin = 2,5 cm; ta có độ mảnh của thanh là:

.l 

imin

1.2

2,5.102

 80

Tra bảng quan hệ giữa  và  ta được  = 0,75. Hệ số này khác với hệ số  đã chọn ban đầu. Nên ta phải chọn lại.

b) Lần chọn 2:

Ta giả thiết:

 0,5  0,75  0,625

2

Từ đó ta tìm được

230.103

4 2

A  26, 2.10 m

0, 625.140.106

Tra bảng thép định hình ta tìm được thép chữ I số 20 với

min

Độ mảnh lúc đó bằng:

F 2, 64cm2 ; i

2, 06cm

 1..2 2,06.102

 97

Tra bảng ta tìm được  = 0,627 gần đúng với giá trị 0,625 theo giả thiết

ban đầu.

Ta kiểm tra lại điều kiện ổn định:

n

N 

230.103 6 2 6 2

.A 

Hay

0, 627.26, 4.104  139.10

N / m

 140.10

N / m

Vậy ta chọn thép chữ I số 20.

3.10. CHỌN HÌNH DẠNG HỢP LÝ CỦA MẶT CẮT VÀ VẬT LIỆU

Đối với thanh chịu kéo – nén đúng tâm để đảm bảo điều kiện bền thì chỉ cần mặt cắt ngang của thanh có diện tích tối thiểu nào đó là đủ. Còn hình dáng mặt cắt nói chung có thể bất kỳ.

Nhưng để đảm bảo điều kiện ổn định thì không phải chỉ chú trọng đến diện tích của mặt cắt ngang mà còn phải chú ý đến hình dáng của nó. Phải chọn hình dáng của mặt cắt sao cho với một diện tích nhất định, thanh chịu được lực nén lớn nhất. Hình dáng đó gọi là hình dáng hợp lý của mặt cắt ngang vì nó đảm bảo được an toàn, tiết kiệm đồng thời tận dụng được khả năng chịu lực của vật liệu.

Như đã biết: 

2 E , nếu càng lớn thì càng giảm, thanh càng dễ mất ổn

th 2 th

định. Do đó để tăng tính ổn định thì cần giảm độ mảnh của thanh:

l

imin

Để giảm thì có thể giảm l, thay đổi liên kết ở hai đầu thanh, tăng trị số imin.

Do vậy, mặt cắt ngang có hình dáng hợp lý khi:

- imin imax Imin Imax . Tức là mặt cắt ngang của thanh là đa giác đều.

- Với cùng diện tích, các mô men quán tính trung tâm càng lớn càng tốt. Vì vậy người ta thường dùng các hình rỗng. Tuy nhiên mặt cắt ngang không được quá mỏng tránh hiện tượng mất ổn định cục bộ.

Mặt khác đối với thanh có độ mảnh lớn, đặc trưng cơ học duy nhất ảnh hưởng

đến th

là mô đun đàn hồi E của vật liệu. Do đó, với loại này ta không nên dùng thép

có cường độ cao để tiết kiệm. Còn đối với thanh có độ bền nhỏ và vừa thì giới hạn

chảy và giới hạn bền ảnh hưởng đến vì nó tăng đượcth .

th . Nên dùng thép có cường độ cao là rất có lợi

CÂU HỎI ÔN TẬP CHƯƠNG 3

1. Định nghĩa dạng cân bằng ổn định và dạng cân bằng không ổn định của hệ biến dạng đàn hồi.

2. Nêu những yếu tố thực tế là nguyên nhân nhiễu động đưa thanh chịu nén ra khỏi dạng cân bằng lý tưởng ban đầu.

3. Nêu dấu hiệu mất ổn định của thanh thẳng chịu nén đúng tâm trong bài toán Euler. Khi mất ổn định thanh sẽ bị cong trong mặt phẳng nào?

4. Định nghĩa độ mảnh của thanh thẳng. Tại sao ta có thể nói: độ mảnh là một đặc trưng quan trọng trong tính toán ổn định của thanh? Độ mảnh phụ thuộc vào những yếu tố nào?

5. Viết và giải thích các đại lượng trong công thức tính ứng suất tới hạn, lực tới hạn của thanh có độ mảnh lớn, độ mảnh vừa, độ mảnh bé. Công thức xác định các độ mảnh giới hạn 0, 1.

1. Trình bày cách lập bảng để tính hệ số giảm ứng suất cho phép .

3.Viết điều kiện ổn định theo hệ số . Nêu các bước giải quyết bài toán kiểm tra ổn định của thanh thẳng chịu nén đúng tâm theo cách này.

4. Tại sao có thể nói cách viết điều kiện ổn định theo hệ số  có độ tin cậy, chuẩn xác cao hơn cách viết điều kiện ổn định theo ứng suất tới hạn cho phép.

9. Nêu đặc điểm của bài toán thanh chịu uốn ngang và uốn dọc đồng thời.

10. Trong phương pháp gần đúng để giải bài toán uốn ngang và uốn dọc đồng thời, ta giả thiết trước dạng độ vòng. Dạng giả thiết này phải tuân theo những điều kiện gì? Nêu dạng độ vòng của thanh có liên kiết khớp ở hai đầu, thanh công xôn.

11. Vì sao khi thanh chịu uốn ngang và uốn dọc đồng thời cần viết điều kiện bền theo tải trọng có kể đến hệ số an toàn mà không viết theo ứng suất cho phép.

12. Trình bày hiện tượng ổn định và mất ổn định của dạng cân bằng chịu uốn.

13. Khi giải bài toán ổn định theo phương pháp Euler, nói một cách tổng quát, ta đã dựa vào điều kiện nào để xác định tải trọng giới hạn.

14. Xác định lực tới hạn và ứng suất tới hạn bằng công thức Euler đối với các thanh có:

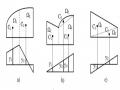
a) Mặt cắt hình chữ nhật (9 4) cm2, chiều dài thanh l=2m (hình 3.14a).

b) Mặt cắt chữ I số 16, chiều dài thanh l=3m (hình 3.14b)

c) Mặt cắt hình chữ nhật rỗng có các cạnh ngoài (20 12) cm2, bề dày vách bằng 2 cm (hình 3.14c).

a) b) c)

N

N

l=3m

l=12m

N

l=2m

Hình 3.14

15. Tìm lực cho phép P đối với một cột bằng gỗ mặt cắt hình chữ nhật (0,2 x 0,1)m2, chịu nén đúng tâm. thanh có chiều dài l = 2m.

Hệ số an toàn về ổn định yêu cầu n = 4. Mô đun đàn hồi của gỗ E = 104MN/m2

(Hình 3.15)

P

y

x

0,2m

l

0,1m

Hình 3.15

Chương 4

TẢI TRỌNG ĐỘNG

4.1. KHÁI NIỆM CHUNG

4.1.1. Tải trọng tĩnh, tải trọng động

Khi thanh biến dạng dưới tác động của các ngoại lực, các phần tử vật chất trong thanh sẽ chuyển động, phát sinh gia tốc chuyển động và kèm theo đó lực quán tính. Bản chất của mọi quá trình đều là động, tuy nhiên để đơn giản phép tính, ta cần xem xét một cách hợp lý khi nào có thể bỏ qua và khi nào không thể bỏ qua các hiệu ứng động.

Nếu gia tốc nhỏ, lực quán tính bé thì có thể bỏ qua lực quán tính so với các tải trọng tác dụng. Bài toán khi này gọi là bài toán tĩnh. Còn khi gia tốc biến dạng lớn, không thể bỏ qua lực quán tính so với tải trọng tác động thì bài toán là bài toán động, tải trọng trong trường hợp này được gọi là tải trọng động.

4.1.2. Phân loại tải trọng động

Vì gia tốc là đặc điểm của bài toán động nên ta có thể phân loại tải trọng động theo gia tốc chuyển động.

- Bài toán chuyển động có gia tốc không đổi. Thuộc loại bài toán này trong kỹ thuật là trường hợp chuyển động của các thang máy, vận thăng trong xây dựng, nâng hoặc hạ các vật nặng, trường hợp chuyển động tròn với vận tốc quay là hằng số của các vô lăng hoặc các trục truyền động.

- Bài toán chuyển động có gia tốc thay đổi và là hàm xác định theo thời gian. Một trường hợp riêng thường gặp là trường hợp gia tốc thay đổi tuần hoàn theo thời gian, gọi là dao động. Thuộc loại bài toán này là các bàn rung, đầm dùi, đầm bàn để làm chặt các vật liệu, bài toán dao dộng của các máy công cụ…

- Bài toán va chạm, trong trường hợp này chuyển động xảy ra rất nhanh trong thời gian rất ngắn, luật biến thiên của gia tốc không xác định hoặc không thể biểu diễn bằng những hàm số giải tích thông thường. Thuộc loại này có các bài toán dừng, phanh một cách đột ngột các chuyển động, đóng cọc bằng búa, …

4.1.3. Các giả thiết khi tính toán

Việc giải quyết bài toán động của thanh là một bài toán phức tạp, liên quan nhiều tới tính chất vật liệu, các số liệu thực nghiệm. Trong phạm vi chương trình, ta chỉ tìm hiểu những cách tương đối đơn giản, những bài toán không có mức độ phức tạp lớn hoặc không đòi hỏi lời giải chính xác cao, những trường hợp phổ biến nhất thường gặp trong thực tế kỹ thuật công trình.

Ta chấp nhận những giả thiết như sau:

1- Tính chất vật liệu khi chịu tải trọng tĩnh và khi chịu tải trọng động là như

nhau, chẳng hạn định luật Hooke, các hằng số đàn hồi giữ nguyên không thay đổi.

2 - Chấp nhận các giả thiết về tính chất biến dạng của thanh như khi chịu tải trọng tĩnh, chẳng hạn các giả thiết tiết diện phẳng, giả thiết thớ dọc không tác dụng tương hỗ.

Khi giải quyết bài toán, ta sẽ sự dụng các kết quả các nguyên lý về động lực học như nguyên lý D’Alembert, nguyên lý bảo toàn năng lượng, nguyên lý bảo toàn xung lượng…

- Nguyên lý D’Alembert: Vật thể chuyển động sẽ nằm ở trạng thái tĩnh nếu đặt vào vật thể lực quán tính tỷ lệ với khối lượng và gia tốc chuyển động.

F qt ma (4.1)

- Nguyên lý bảo toàn năng lượng: Khi bỏ qua nhiệt năng và các năng lượng

không hồi phục thì tổng biến thiên động năng K

và biến thiên thế năng U

của hệ

đàn hồi từ trạng thái 1 đến trạng thái 2 bằng công T của ngoại lực sinh ra trong quá trình đó.

K U T (4.2)

- Nguyên lý bảo toàn xung lượng: Động lượng của hệ trước và sau va chạm là một trị số không đổi.

4.2. BÀI TOÁN CÓ GIA TỐC KHÔNG ĐỔI

Với loại bài toán này, ta chỉ cần đặt lực quán tính theo công thức (4.1) vào hệ thì bài toán trở thành bài toán tĩnh và hoàn toàn có thể áp dụng được các công thức đã có trong phần tĩnh để giải bài toán. Nhờ hai giải thiết đã nêu, kết quả nhận được chính là kết quả của bài toán động.

4.2.1. Bài toán kéo vật nặng lên cao nhanh dần đều

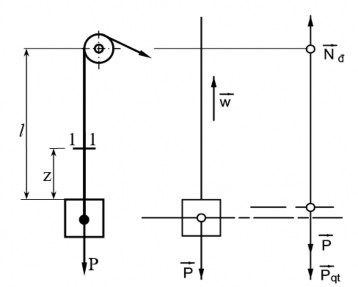
Hình 4.1: Bài toán kéo vật nặng lên cao với gia tốc không đổi

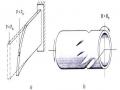
Xét một vật nặng P được kéo lên theo phương thẳng đứng với gia tốc không đổi bởi một dây cáp có mặt cắt F. Trọng lượng bản thân của dây không đáng kể so

với trọng lượng P (hình 4.1).

Áp dụng nguyên lí Đalămbe (d’Alembert) và phương pháp mặt cắt, chúng ta dễ dàng suy ra nội lực trên mặt cắt của dây cáp:

Nđ = P + Pqt

Nđ =

P P w 1w P = KđP (4.3)

g g 



Với Kđ = 1w 

g 



Khi gia tốc w = 0, thì Kđ = 1 và Nđ = Nt = P.

Tải trọng Nt (khi không có gia tốc) là tải trọng tĩnh, tải trọng Nđ (khi có gia tốc) là tải trọng động:

Nđ = KđNt.

Nt

ứng suất mặt cắt của dây khi không có gia tốc t, khi có gia tốc là ứng suất động đ. Vì dây chịu kéo đúng tâm, nên:

Nd

d A

Kd A

Kdt

(4.4)

Các công thức (12.3) và (12.4) cho thấy: bài toán với tải trọng động tương đương như bài toán với tải trọng tĩnh lớn hơn Kđ lần. Hệ số Kđ được gọi là hệ số động hay hệ số tải trọng động.

Kết luận: “Như vậy, nói chung, những yếu tố khác nhau giữa tải trọng động và tải trọng tĩnh được xét đến bằng hệ số động và việc giải các bài toán với tải trọng động quy về việc xác định các hệ số động đó”.

4.2.2. Bài toán chuyển động quay với vận tốc góc không đổi

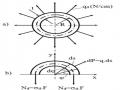
Xét vô lăng có bề dày t rất bé so với đường kính trung bình D = 2R quay với vận tốc góc không đổi (hình 12-2a). Vô lăng có diện tích mặt cắt ngang F, trọng lượng riêng của vật liệu là . Tính ứng suất động của vô lăng.

Ðể đơn giản, ta bỏ qua ảnh hưởng của các nan hoa và trọng lượng bản thân vô lăng. Như vậy, trên vô lăng chỉ có lực ly tâm tác dụng phân bố đều qđ

Vì vô lăng quay với vận tốc góc = const, nên gia tốc góc & 0 .

2

Vậy gia tốc tiếp tuyến wt&R  0 và gia tốc pháp tuyến wn= R

Trên một đơn vị chiều dài có khối lượng F, cường độ của lực ly tâm là:

qđ =

F W F 2R FR 2

g n g g

Nội lực trên mặt cắt ngang:

Tưởng tượng cắt vô lăng bởi mặt cắt xuyên tâm. Do tính chất đối xứng, trên mọi mặt cắt ngang chỉ có thành phần nội lực là lực dọc Nđ, ứng suất pháp đ được coi là phân bố đều (vì bề dầy t bé so với đường kính, hình 4.2b)