Nghiên cứu và ứng dụng một số mô hình học máy trong việc hỗ trợ đánh giá rủi ro tài chính

 Chuyển đổi dữ liệu (data transformation): Trong bước này, dữ liệu sẽ được chuyển đổi về dạng phù hợp cho việc khai phá bằng cách thực hiện các thao tác nhóm hoặc tập hợp.

 Khai phá dữ liệu (data mining): Là giai đoạn thiết yếu, trong đó các phương pháp thông minh sẽ được áp dụng để trích xuất ra các mẩu dữ liệu.

 Đánh giá mẫu (pattern evaluation): Đánh giá sự hữu ích của các mẫu biểu diễn tri thức dựa vào một số phép đo.

 Trình diễn dữ liệu (Knowlegde presentation): Sử dụng các kỹ thuật trình diễn và trực quan hoá dữ liệu để biểu diễn tri thức khai phá được cho người sử dụng.

Các kỹ thuật khai phá dữ liệu thường được chia thành 2 nhóm chính:

 Kỹ thuật khai phá dữ liệu mô tả: có nhiệm vụ mô tả về các tính chất hoặc các đặc tính chung của dữ liệu trong CSDL hiện có.

 Kỹ thuật khai phá dữ liệu dự đoán: có nhiệm vụ đưa ra các dự đoán dựa vào các suy diễn trên dữ liệu hiện thời.

Dưới đây giới thiệu 3 phương pháp thông dụng nhất là: phân cụm dữ liệu, phân lớp dữ liệu và khai phá luật kết hợp.

 Phân cụm dữ liệu: Mục tiêu chính của phương pháp phân cụm dữ liệu là nhóm các đối tượng tương tự nhau trong tập dữ liệu vào các cụm sao cho các đối tượng thuộc cùng một lớp là tương đồng còn các đối tượng thuộc các cụm khác nhau sẽ không tương đồng.

 Phân lớp dữ liệu và hồi quy: Mục tiêu của phương pháp phân lớp dữ liệu là dự đoán nhãn lớp cho các mẫu dữ liệu. Quá trình phân lớp dữ liệu thường gồm 2 bước: Thứ nhất, xây dựng mô hình, một mô hình sẽ được xây dựng dựa trên việc phân tích các mẫu dữ liệu sẵn có. Mỗi mẫu tương ứng với một lớp, được quyết định bởi một thuộc tính gọi là thuộc tính lớp. Thứ hai, sử dụng mô hình để phân lớp dữ liệu, tính độ chính xác của mô hình. Nếu độ chính xác là chấp nhận được, mô hình sẽ được sử dụng để dự đoán nhãn lớp cho các mẫu dữ liệu khác trong tương lai.

 Khai phá luật kết hợp: mục tiêu của phương pháp này là phát hiện và đưa ra các mối liên hệ giữa các giá trị dữ liệu trong CSDL. Mẫu đầu ra của giải thuật khai phá dữ liệu là tập luật kết hợp tìm được.

Khai phá luật kết hợp được thực hiện qua 2 bước: Thứ nhất, tìm tất cả các tập mục phổ biến, một tập mục phổ biến được xác định qua tính độ hỗ trợ và thoả mãn độ hỗ trợ cực tiểu. Thứ hai, sinh ra các luật kết hợp mạnh từ tập mục phổ biến, các luật phải thoả mãn độ hỗ trợ cực tiểu và độ tin cậy cực tiểu.

2.2 Phân lớp

2.2.1 Giới thiệu về phân lớp

Phân lớp (Classification) là việc phân loại các mẫu thành một tập rời rạc của các nhóm có thể. Phân lớp là một quá trình gồm hai bước. Ở bước thứ nhất, mô hình được học mô tả một tập hợp được định trước của các lớp dữ liệu. Mô hình này được xây dựng bằng cách phân tích các thuộc tính của dữ liệu. Mỗi dữ liệu được giả thiết rằng thuộc một lớp đã định nghĩa trước, và được xác định bởi nhãn của lớp (class lable). Trong phân lớp, dữ liệu được phân tích để xây dựng một mô hình tập hợp từ tập dữ liệu huấn luyện (training data set). Dữ liệu riêng lẻ tạo ra tập huấn luyện còn được gọi là mẫu huấn luyện (training examples) và được chọn ngẫu nhiên. Nếu các mẫu huấn luyện được đánh nhãn, bước này còn được gọi là học có giám sát (Supervised learning). Nó đối lập với học không giám sát (unsupervised learning), thường được gọi là phân cụm, trong đó nhãn cho mẫu huấn luyện là không biết và số lượng tập hợp của các lớp được học có thể không biết. Một số mô hình học thông dụng được sử dụng nhiều trong thực tế là luật kết hợp, cây quyết định (Decision tree), mạng nơron, SVM

…

Bước thứ hai là sử dụng mô hình đã được xây dựng ở bước một để phân loại các mẫu dữ liệu chưa có nhãn vào lớp tương ứng. Đầu tiên sẽ đánh giá sự chính xác khi dự đoán. Có một số cách để đánh giá sự chính xác. Cách thường được dùng là phương pháp tiếp cận holdout, nó đánh giá sự chính xác dự báo của mô hình bằng việc đo độ chính xác trên một tập các mẫu mà tập này không được phép dùng khi xây dựng mô hình. Tập như vậy được gọi là tập thử (test data set). Những mẫu này được chọn ngẫu nhiên và độc lập với tập huấn luyện. Sự chính xác của mô hình dựa trên tập dữ liệu kiểm tra là phần trăm của tập mẫu test mà phân loại chính xác bởi mô hình. Với mỗi mẫu thử, nhãn đã biết của lớp được so sánh với sự dự đoán của mô hình học của lớp. Thuật toán học có thể dẫn tới lạc lối bởi những lỗi ngẫu nhiên và sự trùng lặp bên trong tập dữ liệu huấn luyện. Do đó, tập dữ liệu xác nhận có thể được kỳ vọng để cung cấp một sự kiểm tra an toàn chống lại việc over fitting các đặc trưng giả mạo của tập dữ liệu huấn luyện (đó là, mô hình học có thể phân loại một số trường hợp dị thường đặc biệt của dữ liệu thử mà chưa từng xuất hiện trong tập huấn luyện).

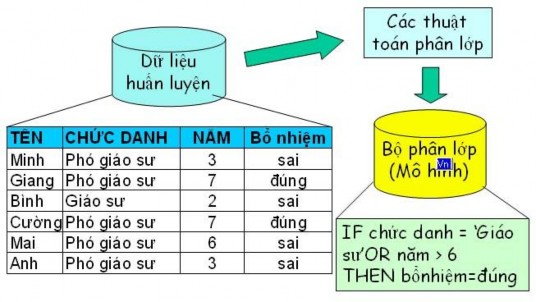
Hình 2-1 Mô hình phân lớp tiêu chuẩn

Tất nhiên, điều quan trọng là tập huấn luyện là đủ lớn để mô hình tự nó có thể học được phân bổ tốt nhất có thể của dữ liệu. Để giải quyết vấn đề này, phương pháp thường được áp dụng khi bộ dữ liệu không đủ lớn mà vẫn tăng khả năng phân lớp là sử dụng xác nhận chéo. Trong xác nhận chéo k-fold, dữ liệu có sẵn được phân thành k tập riêng lẻ với kích cỡ xấp xỉ nhau. Thủ tục xác nhận chéo tạo ra k sự lặp lại trong đó phương pháp học được đưa ra k-1 tập con để sử dụng như là dữ liệu huấn luyện, và nó được kiểm tra trên tập bên trái. Độ chính xác của xác nhận chéo của thuật toán đưa ra thường đơn giản là trung bình cộng của các độ đo chính xác từ những fold riêng lẻ.

Tổng số mẫu

Thực nghiệm 1

Có thể bạn quan tâm!

Xem toàn bộ 91 trang tài liệu này.

Thực nghiệm 2

Thực nghiệm 3

Thực nghiệm 4

Mẫu thử

Nếu độ chính xác của mô hình được coi như là chấp nhận được, mô hình có thể được sử dụng để phân lớp các mẫu về sau mà nhãn lớp là chưa biết. Dữ liệu như vậy cũng được biết đến trong học máy như là các dữ liệu chưa biết “unknown” hoặc dữ liệu trước đây chưa tồn tại “previously unseen”.

Để có thể đánh giá được khả năng của một thuật toán phân lớp, người ta đã đề ra một số phép so sánh bao gồm:

- Chất lượng phân lớp: cho biết khả năng mô hình dự đoán chính xác nhãn lớp của dữ liệu không có nhãn.

- Tốc độ (Speed): cho biết chi phí tính toán liên quan trong việc xây dựng và sử dụng mô hình.

- Sự tráng kiện của mô hình (Robustness): cho biết khả năng mô hình tạo ra các dự đoán đúng với các dữ liệu nhiễu và dữ liệu với giá trị không đầy đủ.

- Tính khả chuyển (Scalability): cho biết khả năng xây dựng mô hình một cách hiệu quả với các dữ liệu khác nhau.

- Tính có thể hiểu được (Interpretability): cho biết mức độ chi tiết của thông tin được cung cấp bởi mô hình.

Trong luận văn này, chúng tôi đặc biệt quan tâm tới vấn đề chất lượng phân lớp và tính có thể hiểu được.

Độ đo chất lượng phân lớp tiêu chuẩn thể hiện thông qua độ chính xác (accuracy), độ hồi nhớ (recall) và độ đúng đắn (precision). Chúng được định nghĩa dựa trên công thức như hình dưới. Chúng ta xem các lớp trong một vấn đề phân lớp nhị phân như là lớp dương “possitive” và âm “negative” tương ứng.

Bảng 2-1 Ma trận hỗn hợp trong phân lớp

Mẫu

Phân lớp dương	Phân lớp âm
Lớp dương thực tế	n00	n01
Lớp âm thực tế	n10	n11

Trong đó: accuracy =

n 00  n11

n 00  n 01  n10  n11

; recall =

n 00

n 00  n 01

; precision =

n 00

n 00  n10

Tính có thể hiểu được thường được tính trong kích thước của các bộ phân lớp.

2.2.2 Các phương pháp phân lớp

Có rất nhiều phương pháp phân lớp, mỗi phương pháp phân lớp đều có cách tính toán khác nhau. Sự khác nhau cơ bản của các phương pháp này là ở thuật toán học quy nạp. Tuy nhiên, nhìn một cách tổng quan thì các phương pháp đó đều phải thực hiện một số bước chung như sau: đầu tiên, mỗi phương pháp sẽ dựa trên các thông tin của các mẫu để biểu diễn mẫu thành dạng vector; sau đó, tuỳ từng phương pháp mà ta sẽ áp dụng công thức và phương thức tính toán khác nhau để thực hiện việc phân loại.

Sau đây là một số cách tiếp cận mà theo thực nghiệm thì có hiệu quả phân loại cao cũng như những thuận lợi và bất tiện của mỗi cách.

Phương pháp k người láng giềng gần nhất (k-NN Algorithm):

Ý tưởng:

Là phương pháp nổi tiếng về hướng tiếp cận dựa trên xác suất thống kê. Khi cần phân loại mẫu mới, thuật toán sẽ tính khoảng cách (khoảng cách Euclide, Cosine...) của tất cả các mẫu trong tập huấn luyện đến mẫu mới này để tìm ra k mẫu gần nhất (gọi là k “láng giềng”) sau đó dùng các khoảng cách này đánh trọng số cho tất cả các mẫu. Trọng số của một mẫu chính là tổng tất cả các khoảng cách ở trên của mẫu trong k láng giềng có cùng đặc trưng, đặc trưng nào không xuất hiện trong k láng giềng sẽ có trọng số bằng không. Sau đó các đặc trưng được sắp xếp theo mức độ trọng số giảm dần và các đặc trưng có trọng số cao sẽ được chọn là đặc trưng của mẫu cần phân loại.

Ưu điểm:

Có một vài thuận lợi khi thực thi giải pháp này. Giải thuật này được xem như giải thuật tốt nhất để bắt đầu việc phân loại mẫu và là một giải thuật mạnh.

Một trong những thuận lợi của giải thuật này chính là sự rõ ràng và dễ dàng, đơn giản và dễ thực hiện. Được dựa trên phương pháp trực tuyến với cách xử lý một số hỗn hợp các mẫu. Đặc biệt, giải thuật này còn kiểm tra các mẫu kề các mẫu mới, và cần vài thông số để làm việc này, nói cách khác giải thuật này hầu như không giới hạn. Dựa vào các nhân tố này, giải thuật này hoàn toàn hiệu quả thông qua thực nghiệm và dễ dàng áp dụng.

Một lợi ích nữa của k-NN là giải thuật này có thể được vận dụng để cải tiến hơn. Nói cách khác, giải thuật này nhanh chóng chỉnh sửa và phù hợp với các trường hợp khác. Ví dụ, giải thuật có thể được áp dụng cho bất kỳ khoảng cách đo lường nào khi nhập vào và các mẫu huấn luyện vì khoảng cách của các mẫu nhập vào có thể được giảm đi để cải tiến hiệu quả của giải thuật, do vậy k-NN có thể được áp dụng cho mẫu với bất kì khoảng cách nào trong mẫu đào tạo. Cũng vì thế mà hầu hết thời gian huấn luyện đòi hỏi cho phân loại mẫu trong giải thuật k-NN; giải thuật này được đánh giá là kỹ thuật chi phí trong các kỹ thuật. cuối cùng, k-NN là giải thuật mạnh có thể giám sát các nguồn tiềm năng lỗi.

Nhược điểm:

Rất khó có thể tìm ra k tối ưu. Hơn nữa với trường hợp mẫu có nhiễu thì việc phân loại là không tốt

Phương pháp Cây quyết định (Decision Tree Algorithm):

Ý tưởng:

Bộ phân lớp cây quyết định là một dạng cây mà mỗi nút được gán nhãn là một đặc trưng, mỗi nhánh là giá trị trọng số xuất hiện của đặc trưng trong mẫu cần phân lớp, và mỗi lá là nhãn của phân lớp. Việc phân lớp của một mẫu dj sẽ được duyệt đệ qui theo trọng số của những đặc trưng có xuất hiện trong mẫu dj. Thuật toán lặp đệ qui đến khi đạt đến nút lá và nhãn của dj chính là nhãn của nút lá tìm được. Thông thường việc phân lớp mẫu nhị phân sẽ tương thích với việc dùng cây nhị phân.

Ưu điểm:

- Dễ hiểu, dễ cài đặt.

- Có thể chấp nhận trường hợp tập dữ liệu huấn luyện có nhiễu, và cho hiệu quả phân loại tương đối cao.

Nhược điểm:

Việc sử dụng giải thuật cây quyết định liên quan đến một số hạn chế quan trọng, dựa vào trạng thái nguyên thuỷ của thuật toán mà chia các vùng mẫu được đưa vào các tập hợp con. Trước tiên, giải thuật này chia những tập mẫu tuỳ thuộc vào đặc trưng (một bộ phận từ ) mọi lúc, bằng cách sử dụng các đặc trưng rõ ràng mọi lúc. Dựa vào các nhân tố này, giải thuật này sẽ bị sai nếu một lỗi bị nhìn thấy tại bất cứ mức độ nào, bởi vì cây con bên dưới cấp bậc sẽ bị sai. Do đó, giải thuật cây quyết định không mạnh và nó dường như mạo hiểm để quyết định những nhánh phân loại.

Một vấn đề khác là không có bảo vệ phù hợp giống như Support Vector Machines, vì vậy chúng có thể loại trừ các đặc trưng. Điều này có nghĩa là chúng không thể chấp nhận một mẫu với số lượng lớn đặc trưng như SVM, vì có quá nhiều đặc trưng tạo nên tràn phù hợp và làm cho khả năng học kém hơn.

Một trở ngại khác là thời gian huấn luyện phân loại cao bởi vì giải thuật này cần so sánh tất cả những nhánh con có thể, nên mất nhiều thời gian để chia và duyệt các đặc trưng.

Phương pháp Naïve Bayes

Ý tưởng :

Ý tưởng cơ bản của phương pháp xác suất Bayes là dựa vào xác suất có điều kiện của từ hay đặc trưng xuất hiện trong mẫu với đặc trưng để dự đoán đặc trưng của mẫu đang xét. Điểm quan trọng cơ bản của phương pháp này là các giả định độc lập:

- Các từ hay đặc trưng của mẫu xuất hiện là độc lập với nhau.

- Vị trí của các từ hay các đặc trưng là độc lập và có vai trò như nhau. Giả sử ta có:

- n đặc trưng (lớp) đã được định nghĩa

c1, c2 , , cn

- Mẫu mới cần được phân loại d j

Để tiến hành phân loại mẫu

d j , chúng ta cần phải tính được tần suất xuất hiện

của các lớp

ci (i  1,2,...,n)

trong mẫu

d j . Sau khi tính được xác suất của mẫu đối

với các đặc trưng, theo luật Bayes, mẫu sẽ được phân lớp vào đặc trưng ci

suất cao nhất.

Thuận lợi:

nào có xác

Là phương pháp đơn giản, cài đặt không phức tạp, tốc độ nhanh, với tập huấn luyện lớn thì cho kết quả vẫn tương đối chính xác.

Nhược điểm:

Giải thuật Naïve Bayes cũng có những điểm yếu riêng mặc dù được xem là trình diễn tốt hơn giải thuật Cây quyết định.

Một trong những trở ngại là dựa trên luật gọi là các điều kiện độc lập. Có thể bị vi phạm bởi các trường hợp trong thực tế, bởi vì Naïve Bayes thừa nhận các đặc trưng trong mẫu độc lập riêng rẽ và được biểu diễn một cách nghèo nàn khi những đặc trưng này có mối liên hệ với nhau. Hơn nữa, luật này không tạo được sự thường xuyên cho việc xuất hiện các đặc trưng. Một bất lợi khác nữa là giải thuật sử dụng nhiều tính toán và vì vậy thời gian bị chi phối.

Phương pháp mạng Nơron (Neural Network):

Ý tưởng:

Mô hình mạng neural gồm có ba thành phần chính như sau: kiến trúc (architecture), hàm chi phí (cost function), và thuật toán tìm kiếm (search algorithm). Kiến trúc định nghĩa dạng chức năng (functional form) liên quan giá trị nhập (inputs) đến giá trị xuất (outputs).

Kiến trúc phẳng ( flat architecture ) : Mạng phân loại đơn giản nhất ( còn gọi là mạng logic) có một đơn vị xuất là kích hoạt kết quả (logistic activation) và không có lớp ẩn, kết quả trả về ở dạng hàm (functional form) tương đương với mô hình hồi quy logic. Thuật toán tìm kiếm chia nhỏ mô hình mạng để thích hợp với việc điều chỉnh mô hình ứng với tập huấn luyện. Ví dụ, chúng ta có thể học trọng số trong mạng kết quả (logistic network) bằng cách sử dụng không gian trọng số giảm dần (gradient descent in weight space) hoặc sử dụng thuật toán interated-reweighted least squares là thuật toán truyền thống trong hồi quy (logistic regression).

Kiến trúc môđun (modular architecture): Việc sử dụng một hay nhiều lớp ẩn của những hàm kích hoạt phi tuyến tính cho phép mạng thiết lập các mối quan hệ giữa những biến nhập và biến xuất. Mỗi lớp ẩn học để biểu diễn lại dữ liệu đầu vào bằng cách khám phá ra những đặc trưng ở mức cao hơn từ sự kết hợp đặc trưng ở mức trước.

2.3 Mạng Nơron

Một trong những kỹ thuật tiên tiến được sử dụng trong việc tạo quyết định tài chính là mạng Nơron. Mục này sẽ giới thiệu về mạng nơron được tạo và hoạt động như thế nào.

Các mạng nơron nhân tạo được tạo ra nhằm mục đích mô phỏng lại bộ não của con người. Có thể coi bộ não là một máy tính hay một hệ thống xử lý thông tin song song, phi tuyến và cực kỳ phức tạp. Nó có khả năng tự tổ chức các bộ phận cấu thành của nó, như là các tế bào thần kinh (nơron) hay các khớp nối thần kinh (synapse), nhằm thực hiện một số tính toán như nhận dạng mẫu và điều khiển vận động nhanh hơn nhiều lần các máy tính nhanh nhất hiện nay. Sự mô phỏng bộ não con người của mạng nơron là dựa trên cơ sở một số tính chất đặc thù rút ra từ các nghiên cứu về thần kinh sinh học. Lý thuyết về Mạng nơ ron nhân tạo, hay gọi tắt là “Mạng nơ ron”, được xây dựng xuất phát từ một thực tế là bộ não con người luôn luôn thực hiện các tính toán một cách hoàn toàn khác so với các máy tính số.

2.3.1. Mô hình một nơron perceptron

Một nơron perceptron là một phần tử xử lý gồm:

 n đầu vào xi, mỗi đầu vào ứng với một giá trị thực wi gọi là trọng số.

 Một giá trị thực b gọi là ngưỡng (bias).

 Một hàm kích hoạt f.

 Giá trị ra y.

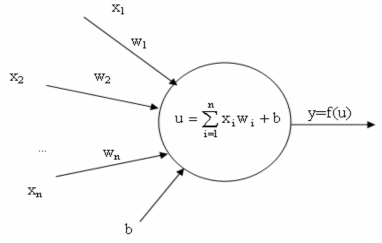
Hình 2-2 Mô hình một nơron perceptron