Xác Định Giá Trị Của Luật Hợp Thành

2.4.3.1 Xác định giá trị của luật hợp thành

Xét luật hợp thành gồm n mệnh đề hợp thành:

R1: IF A1 = X11 AND … AND Am=X1m THEN B=Y1 hoặc R2: IF A1 = X21 AND … AND Am=X2m THEN B=Y2 hoặc

…

Rn: IF A1 = Xn1 AND … AND Am=Xmn THEN B=Yn

Nếu vector các giá trị rõ đầu vào x0k, k=1,2,..,n là đã biết trước thì theo công thức (2.6a) hoặc (2.6b), mỗi một mệnh đề hợp thành trong luật hợp thành trên sẽ có một giá trị là một tập mờ Ri với hàm thuộc Ri(y)=AiB(y), i=1,2,..,n. Vì luật hợp thành đang xét có n mệnh đề hợp thành nên ta cũng có n tập mờ Ri. Vấn đề đặt ra là từ n tập mờ Ri, i=1,2,..,n đó ta phải xác định được tập mờ kết quả chung R cho toàn bộ luật hợp thành theo phép tính hợp các tập hợp Ri

n

Có thể bạn quan tâm!

• Phân Tích Kỹ Thuật Trong Dự Báo Thị Trường Chứng Khoán.
• Nghiên cứu và ứng dụng một số mô hình học máy trong việc hỗ trợ đánh giá rủi ro tài chính - 4
• Mô Hình Mạng Perceptron 3 Lớp (Mlp)
• Phân Kỳ Và Hội Tụ Của Đường Trung Bình Di Động
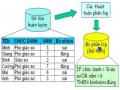
• Kết Hợp Hạng, Các Chỉ Số Và Luật Mờ Tương Ứng
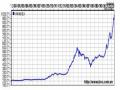
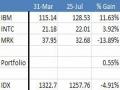
• Kết Quả So Sánh Giữa Quyết Định Từ Macd, Mô Hình Và Thực Tế

Xem toàn bộ 91 trang tài liệu này.

R Ri

i1

(2.7)

Lý do cho việc sử dụng phép hợp là vì các mệnh đề hợp thành trong một luật hợp thành được liên kết với nhau bằng toán tử “hoặc”.

Giống như đã làm với phép suy diễn, để thực hiện công thức (2.7) cho n tập mờ Rq, ta bắt đầu với tập kinh điển. Cho hai tập kinh điển A và B, gọi A(y) và B(y) là những hàm thuộc của chúng. Tập AB là kết quả hợp của hai tập trên sẽ có hàm thuộc

 (y) = 1 nếu y A

AB 

0

bằng một trong hai công thức :

AB(y) =max(A(y), B(y) ) (2.8a)

AB(y) =min(A(y) + B(y) ) (2.8b)

vì chúng tương đương

Khi A và B không là tập kinh điển mà là hai tập mờ thì do các hàm thuộc

A(y)và B(y) của chúng không còn là hàm hai trị tại 0 và 1 nên tính tương đuơng của (2.8a) và (2.8b) cũng mất. Ta phải quyết định chọn sử dụng công thức nào:

Nếu sử dụng công thức (2.8a) thì ta nói phép hợp các tập mờ đã được thực hiện theo luật Max.

Nếu sử dụng công thức (2.8b) thì ta nói phép hợp các tập mờ đã được thực hiện theo luật Sum.

2.4.3.2 Phép tích hợp các tập mờ

Ở trên ta đã giới thiệu hai công thức tính hợp của các tập mờ. Một cách tổng quát thì mọi hàm  :[0,1]2 [0,1], đều có thể được sử dụng để xác định hàm thuộc cho AB nếu chúng thoả mãn :

a) (x,y)=(y,x)

b) (x,y)(u,v) nếu xu và yv c) (x,(y,z)) = ((x,y,z))

d) (0,x) = x

trong đó x,y,u,v,z [0,1]

2.4.4 Giải mờ

Sau khi tính xong giá trị luật hợp thành ta thu được kết quả là tập mờ R(y). Kết quả đó chưa thể là một giá trị thích hợp để điểu khiển. Công việc của chúng ta là phải xác định một giá trị rõ y0 từ tập mờ R(y) của nó, đó là việc giải mờ. Giá trị rõ y0 xác định được có thể xem như "phần tử đại diện xứng đáng" cho tập mờ.

Căn cứ những quan niệm khác nhau về phần tử đại diện xứng đáng mà ta sẽ có các phương pháp giải mờ khác nhau. Người ta thường sử dụng hai phương pháp chính, đó là: phương pháp điểm cực đại và phương pháp điểm trọng tâm.

2.4.4.1 Phương pháp điểm cực đại

Tư tưởng chính của phương pháp này là tìm trong tập mờ có hàm thuộc R(y) một phần tử rõ y0 với độ phụ thuộc lớn nhất( có xác suất thuộc tập mờ lớn nhất trong số những phần tử còn lại), tức là :

y0=arg max R(y) (2.9)

Tuy nhiên, do việc tìm y0 theo 13 có thể đưa đến vô số nghiệm nên ta cần đưa thêm những yêu cầu cho phép chọn trong số các nghiệm đó một giá trị y0 cụ thể chấp nhận được. Như vậy, việc giải mờ theo phương pháp cực đại sẽ gồm hai bước :

Xác định miễn chứa giá trị rõ y0. Giá trị này là giá trị mà tại đó hàm thuộc đạt giá trị cực đại G={y Y | R(y)=H}

Xác định y0 có thể chấp nhận đc từ G

Trong trường hợp có vô số nghiệm thì để tìm y0 ta có hai cách :

1) Xác định điểm trung bình

y0= y1 y2

2

Nếu các hàm thuộc đều có dạng tam giác hoặc hình thang thì điểm y0 xác định theo phương pháp này sẽ không quá bị nhạy cảm với sự thay đổi của giá trị rõ đầu vào x0 do đó rất thích hợp với các bài toán có nhiều biên độ nhở ở đầu vào.

2) Xác định điểm cận trái hoặc phải

y0=inf(y) yG hoặc y0 = sup(y) yG

Theo phương pháp giải mờ này, nếu các hàm thuộc đều có dạng tam giác hoặc hình thang thì điểm y0 sẽ phụ thuộc tuyến tính(trong một lân cận) vào giá trị rõ x0 tại đầu

vào

R(y)

H

y

R(y)

G

y

H

y0 y1 y2

Hình 2-5 Giải mờ bằng phương pháp cực đại

2.4.4.2 Phương pháp điểm trọng tâm

Phương pháp điểm trọng tâm sẽ cho ra kết quả y0 là hoành độ của điểm trọng tâm miền được bao bởi trục hoành và đường R(y)

yR ( y)dy

y0=S

R( y)dy

S

Với S=supR(y)={y|R(y)0} là miền xác định của tập mờ R

R(y) R(y)

y0 y0

(2.10)

Hình 2-6 Giải mờ bằng phương pháp điểm trọng tâm

Đây là phương pháp hay được sử dụng nhất. Nó cho phép ta xác định giá trị y0 với sự tham gia của tất cả các tập mờ đầu ra của luật điều khiển một cách bình đẳng và chính xác. Tuy nhiên phương pháp này lại không để ý được tới toạ độ thoản mãn của mệnh đề điều khiển cũng như thời gian tính lâu. Ngoài ra nó còn có nhược điểm là giảtị yo xác định lại có độ thuộc nhỏ nhất, thậm chí bằng 0.

2.4.5 Hệ suy diễn mờ

Đầu vào

Đầu ra

(rõ)

(rõ)

Giải mờ(5)

Cơ sở tri thức

CSDL(2)

Luật cơ sở(1)

Mờ hoá(4)

(mờ)

Khối tạo quyết(3)

(mờ)

Hình 2-7 Hệ suy diễn mờ

Hệ suy diễn mờ còn được gọi là hệ dựa trên tập luật mờ, mô hình mờ. Về căn bản một hệ suy diễn mờ được hợp thành từ năm khối được mô tả như hình trên.

1) Một bộ luật cơ sở bao gồm một số các luật dạng if-then

2) Cơ sở dữ liệu dùng để định nghĩa các hàm thuộc của các tập mờ được sử dụng trong các luật mờ

3) Khối tạo quyết định thực hiện các thao tác suy diễn dựa trên các luật

4) Bộ mờ hoá được dùng để chuyển các giá trị đầu vào sang các mức hợp với với giá trị không rõ của ngôn ngữ

5) Bộ giải mờ chuyển các kết quả mờ của việc suy diễn sang các giá trị đầu ra

rõ thức.

Thông thường luật cơ sỏ và cơ sở dữ liệu được kết hợp và gọi chung là cơ sở tri Các bước của suy diễn được thực hiện bởi hệ suy diễn mờ:

 So sánh các biến đầu vào với các hàm thuộc dựa vào phần tiên đề để xác định các giá trị thuộc của từng nhãn trong ngôn ngữ tự nhiên. (Bước này thường được gọi là mờ hoá)

 Kết hợp các giá trị thuộc để có được trọng lượng của từng luật

 Sinh các kết quả thoả mãn (cả mờ và rõ) cho từng luật dựa vào trọng lượng.

 Kết hợp các kết quả thoả mãn để có được đầu ra rõ (bước này được gọi là mờ hoá).

Kết luận

Chương này đã giới thiệu tổng quan về khai phá dữ liệu, phân lớp và các phương pháp phân lớp hay dùng hiện nay. Chúng tôi đã giới thiệu khá chi tiết về mạng nơron và hệ mờ. Đây chính là các kiến thức chính để xây dựng mô hình ở các chương sau.

Chương 3 - MÔ HÌNH PHÂN TÍCH RỦI RO TÀI CHÍNH

2.1 Sơ lược về mô hình

Chúng tôi đã xây dựng mô hình dựa trên việc kết hợp phân lớp bằng mạng nơron với logic mờ và phân tích kỹ thuật. Sự kết hợp này sẽ cho ta một hệ hỗ trợ quyết định với kết quả cuối cùng là hành động mua, bán, hoặc giữ lại một loại cổ phiếu nào đó. Sơ đồ tóm tắt các thành phần chính của mô hình của chúng tôi được trình bày trong hình 3-1 dưới đây.

Dữ liệu

Lựa chọn đặc trưng

Luật cơ sở

Phân lớp dữ liệu

Biểu đồ +

Phân tích kỹ thuật

Hành động mua bán

Hệ hỗ trợ quyết định

Hình 3-1 Mô hình đề xuất

Mô hình đề xuất gồm hai mô đun:

- Phân lớp dữ liệu nhằm đánh giá và dự báo rủi ro trong kinh doanh.

- Xây dựng hệ hỗ trợ quyết định nhằm đánh giá và hỗ trợ người dùng.

2.2 Phân lớp dữ liệu - Thiết kế mạng nơron

Công việc của chúng ta không đơn thuần chỉ là đánh giá và dự báo rủi ro của một công ty duy nhất mà là đánh giá rủi ro một tập hợp các công ty. Do đó, trước hết chúng ta thực hiện công việc phân lớp các công ty và dự báo rủi ro trong thời gian tiếp theo. Việc thiết kế một mạng nơron dự báo thành công dữ liệu tài chính là một công việc phức tạp bao gồm các bước sau:

- Chọn biến

- Thu thập dữ liệu

- Tiền xử lý dữ liệu

- Phân hoạch dữ liệu

- Thiết kế mạng nơron

- Huấn luyện mạng

- Thực hiện phân tích dữ liệu

2.2.1 Chọn loại dữ liệu đầu vào

Dữ liệu tài chính có rất nhiều biến, trong phạm vi dự báo đánh giá rủi ro dựa trên lĩnh vực kinh doanh chứng khoán chúng ta chỉ chọn một số biến sau:

- Ticker: mã công ty

- Date: Ngày giao dịch

- Open: giá mở cửa

- High: giá cao trong ngày

- Close: giá đóng cửa

- Low: giá thấp nhất trong ngày.

Ngoài ra, còn các biến đặc trưng trong báo cáo tài chính làm dữ liệu đầu vào và một số thông tin liên quan tới công ty như tên công ty, công ty thuộc ngành nào…

2.2.2 Thu thập dữ liệu

Thu thập dữ liệu: dữ liệu tài chính gồm các báo cáo tài chính như: bảng cân đối kế toán, báo cáo kết quả kinh doanh, báo cáo lưu chuyển tiền tệ, ngoài ra còn các giao dịch. Các dữ liệu này được công bố trên các sàn cũng như các trang giao dịch chứng khoán. Các báo cáo tài chính có số liệu đã được các tổ chức kiểm toán kiểm tra. Trên

thế giới dữ liệu giao dịch cũng như báo cáo tài chính đã được chuẩn hoá, tuy nhiên ở việt nam dữ liệu này chưa được chuẩn hoá. Do đó quá trình thu thập dữ liệu là tương đối tốn kém thời gian.

2.2.3 Tiền xử lý dữ liệu

Trên thực tế, dữ liệu tài chính trên các thị trường chứng khoán là không minh bạch. Không minh bạch ở đây có nghĩa:

- Không đầy đủ: thiếu giá trị thuộc tính, thiếu thuộc tính cần quan tâm …

- Nhiễu: chứa lỗi hoặc thông tin ngoài luồng

- Mâu thuẫn: chứa các mâu thuẫn giữa mã và tên

Do đó, chúng ta cần chuẩn hoá dữ liệu trước khi khai thác và sử dụng dữ liệu này: Dữ liệu tài chính được đưa vào cơ sở dữ liệu dưới dạng các bảng đã được chuẩn hoá có cấu trúc được trình bày chi tiết trong phụ lục C

Trong đó, bảng Quotes chứa dữ liệu giao dịch trong từng này, luận văn đã thu thập được dữ liệu giao dịch từ năm 2002 tới thời điểm hiện tại

Bảng Balances, Cashflows, Incomes chứ dữ liệu báo cáo tài chính theo quý hoặc theo năm. Cụ thể:

Bảng cân đối kế toán (Balances): cho biết nguồn vốn, tiền, tài sản cố định của doanh nghiệp.

Bảng báo cáo kết quả hoạt động kinh doanh (Incomes): cho biết doanh thu và chi phí trong hoạt động kinh doanh, bán hàng, quản lý doanh nghiệp…

Bảng báo cáo lưu chuyển tiền tệ (Cashflows): liên qua tới thông tin luồng tiền lưu chuyển như thế nào.

Bảng Công ty (Companies): Mô tả các thông tin về công ty như mã niêm yết trên sàn chứng khoán, công ty thuộc ngành nào.

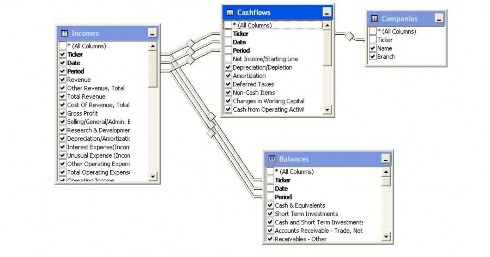
Hình 3-2 Mồ hình thực thể liên kết

Xem tất cả 91 trang.