Vùng Tần Số Cộng Hưởng Dao Động Ngang, Dọc Của Giỏ Trên Nhịp

(phương dây cáp). Vì vậy, nếu chỉ xét dao động ngang của giỏ thì ta có thể xét riêng phương trình này là đủ.

v fz ( t )  2r.g. Dk

, (a)

k

m



k 2r 2 D2

(3.35)

x f ( t )  2 2 1 

x.k 2r.gk

(b)

k r mr  21  2.2 

2r 2 D2 1  2.2









k k k

k  1, n

1) Xét phương trình k

 2r.g.

v 

fz( t )

m

Dk

k

2r2 D2

, với

D vk zk k r

sin,

do đó

2r.g.

Dk

k

2r2 D2

sink

g

cos2 

. Nếu coi

cos2 1 , ta có thể viết gần đúng

k k

phương trình (3.35 a):

v 

fz( t )

g vk zk

k m r

, k  1, n

(3.36)

đặt

a d .H và gọi A 

2a 1

a









0

0

0

a 0 0

2a 1 a 0

a 2a 1 a

0 0 0

0 0 0

0

0

0

a

0

0

0

0

2a 1

a

0 

0 



a 

2a 1

0



mg.s

fz ( t )

v 

m 

1

z1 

v1 

z2 

v2 

v 

f ( t )

z

Z 

; V 

2

; 



, F( t ) m

V 





z 

v 

n 

n 

v 

n 

fz ( t )

m 

Khi đó (3.36) được viết : V

CV F( t )

(3.37)

Trong đó

C gI A1 

gọi là ma trận độ cứng và ở đây C là ma trận đối xứng

r

(do A-1 đối xứng, I là ma trận đơn vị).

Phương trình tần số hay phương trình đặc trưng của (3.37) sẽ là:

C 2 I 0

(3.38)

Các nghiệm k , k = 1, 2, ..., n của (3.38) được gọi là các tần số riêng. Giả sử lực cưỡng bức có dạng: fz ( t ) h.sin( t ) , khi đó nghiệm vi sẽ

chứa các số hạng h sint . Do vậy, nếu có giá trị gần với một nào

k

2 2 k

đó sẽ dẫn đến hiện tượng phách và hiện tượng cộng hưởng.

Phương trình (3.38) để tìm các tần số riêng của (3.37) sẽ được thực hiện trên Matlab, từ đó tìm ra vùng cộng hưởng của (3.35. a).

2) Xét phương trình (3.35b)

x 

f ( t )

2 2  1 

k x.k

2r.gk

r mr  21  2.2 

2r2 D2 1  2.2

k

2

k k

2r2 D2

Nếu ta coi

cos

k 1

k 1 2r2

và thì phương trình

(3.35b) có dạng gần đúng:

g 

x( t ) fx ( t )

(3.39)

k r k

r mr

Phương trình (3.39) có tần số riêng

(3.40)

g

r

x( t )

Vì vậy nếu

hoặc

fx ( t ) có dạng tuần hoàn với chu kỳ khá gần (hoặc

g

r

bằng) thì sẽ có hiện tượng phách hoặc cộng hưởng.

Chú ý rằng các phương trình (3.37) và (3.39) là dạng gần đúng của các phương trình (3.35), vì vậy vùng tần số của (3.37) và (3.39) sẽ là cơ sở ban đầu cho việc sử dụng Matlab trong quá trình tìm vùng cộng hưởng của các phương trình trong (3.35).

Tính toán với các thông số:

- Số lượng giỏ trên nhịp cáp n = 30;

- Lực căng ngang H = 3500 N;

- Độ dài dây treo giỏ r = 0,3 m;

- Khoảng cách giữa hai giỏ S = 0,80 m;

- Khối lượng giỏ m = 2 kg;

- Gia tốc trọng trường g = 9,80 m/s2.

Với các thông số tính toán trên, có được vùng cộng hưởng của (3.37) sẽ là vùng có tần số trong khoảng [ 3,65 5,7] , vùng cộng hưởng của (3.39) ở xung quanh giá trị 3,5.

Xuất phát từ giá các trị tìm được ở trên, sử dụng Matlab tìm được các vùng tần số cộng hưởng cho các dao động ngang và dọc của giỏ khi di chuyển trên nhịp cáp được ghi trên bảng 3.9.

Bảng 3.9. Vùng tần số cộng hưởng dao động ngang, dọc của giỏ trên nhịp

TT

Dao động	Vùng tần số cộng hưởng
1	Dao động ngang	5,5		6,4
2	Dao động dọc	5,4		6,5

Có thể bạn quan tâm!

• Giải Hệ Phương Trình Vi Phân Dao Động Của Giỏ Đựng Trái Thanh Long
• Độ Vòng F (Cm) Tính Theo Lực Căng Ngang H (N) Và (Cm) Khi Tải Trọng Đều Q = 0.2 (N/cm)
• Khảo Sát Độ Vòng Của Đường Cáp Hai Trụ Đỡ Có Độ Cao Chênh Nhau
• Sự Ảnh Hưởng Của Độ Dài Nhịp Cáp Đến Biên Độ Cực Đại Của Dao Động Giỏ Đựng Thanh Long
• Phương Pháp Xác Định Các Đại Lượng Nghiên Cứu Và Thiết Bị Đo
• Bố Trí Thí Nghiệm Đo Lực Căng Ngang Và Độ Vòng Đường Cáp

Xem toàn bộ 196 trang tài liệu này.

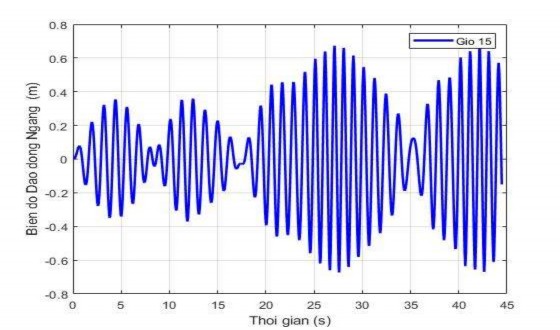
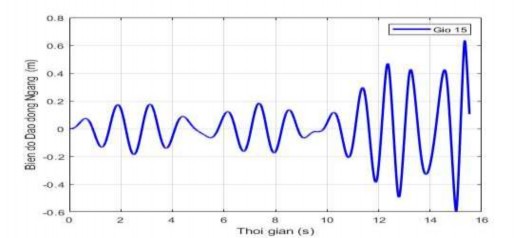
Các hình 3.5 đến hình 3.8 cho các hình ảnh về hiện tượng phách và cộng hưởng của các dao động ngang, dọc của giỏ khi di chuyển trên nhịp cáp.

Hình 3.5. Hiện tượng phách của dao động ngang khi tần số gió fz = 5,4

Hình 3.6. Hiện tượng cộng hưởng của dao động ngang khi tần số gió fz = 5,9

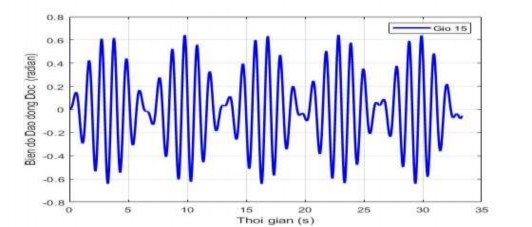
Hình 3.7. Hiện tượng phách của dao động dọc khi tần số gió fx = 5,3

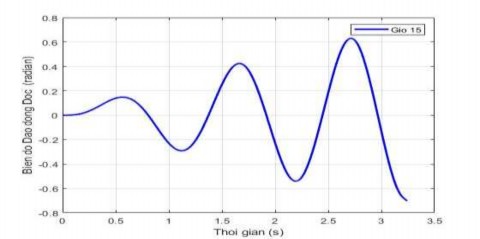
Hình 3.8. Hiện tượng cộng hưởng của dao động dọc khi tần số gió fx = 5,4

3.7.1.2. Xét quá trình giỏ dịch chuyển trên khu vực cáp chuyển hướng

Theo (2.98), khi cáp di chuyển với vận tốc v (m/s) và lực gió tác động lên

giỏ (phương ngang vuông góc với cáp) là f(t), ta có được phương trình dao động của giỏ thanh long trong quá trình di chuyển tại khu vực chuyển hướng :

g a2

f ( t )

2 





r

r( R r.) 

mr 1 2 

(3.41)

với giá trị ban đầu



g

r

0 3,5 , sử dụng Matlab tìm được vùng cộng hưởng

của (3.41) là khoảng [ 5,6 8]. Hình ảnh về hiện tượng phách, cộng hưởng khi giỏ chuyển hướng được thể hiện trên các hình 3.9 và 3.10.

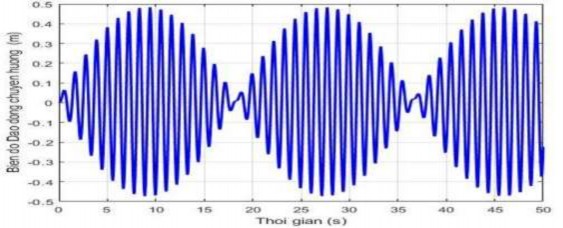
Hình 3.9. Hiện tượng phách của dao động khi giỏ chuyển hướng với tần số gió f = 5,5

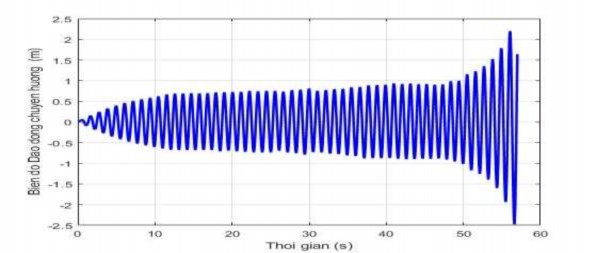
Hình 3.10. Hiện tượng cộng hưởng của dao động khi giỏ chuyển hướng với tần số gió f = 5,6

Nhận xét

+ Việc khảo sát các vùng cộng hưởng của các dao động giỏ giúp cho quá trình tác nghiệp được thuận lợi. Với các thông số khi thiết kế đường cáp, gặp khi gió trời có tần số nằm trong vùng cộng hưởng, ta có thể điều chỉnh độ căng của cáp đề thay đổi lực căng ngang H. Làm như vậy là đã thay đổi vùng cộng hưởng của các dao động giỏ, tránh cho tần số gió rơi vào vùng này.

+ Trong các khảo sát tiếp theo, sẽ tính toán với các lực gió có tần số thấp hơn vùng cộng hưởng.

3.7.2. Khảo sát biên độ dao động cực đại các giỏ đựng thanh long

Giải gần đúng hệ phương trình vi phân cấp một (2.97) trên Matlab, với H = 3500 N, r = 0,3 m, khoảng cách các giỏ S = 0,8m, khối lượng giỏ m = 2 kg, nhịp cáp treo 30 giỏ. Kết quả tính toán về biên độ dao động cực đại của các giỏ ở các vị trị khác nhau được thể hiện trên bảng 3.10. Đồ thị 3.11 biểu diễn biên độ cực đại của các giỏ theo các vị trí được treo trên nhịp cáp.

Bảng 3.10. Biên độ dao động cực đại của các giỏ theo các vị trí treo trên cáp

TT

Biên độ max (cm)	TT	Biên độ max (cm)	TT	Biên độ max (cm)
1	16,614	11	16,723	21	16,684
2	16,624	12	16,736	22	16,668
3	16,633	13	16,745	23	16,663
4	16,642	14	16,751	24	16,656
5	16,649	15	16,753	25	16,649
6	16,656	16	16,751	26	16,642
7	16,663	17	16,745	27	16,633
8	16,668	18	16,736	28	16,624
9	16,684	19	16,723	29	16,614
10	16,706	20	16,706	30	16,614

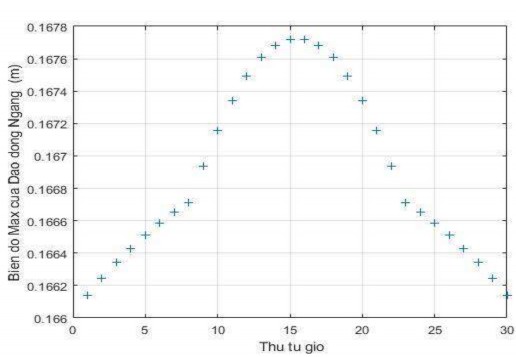
Hình 3.11. Đồ thị biên độ dao động ngang cực đại của giỏ đựng thanh long theo vị trí treo giỏ

Nhận xét: Biên độ dao động cực đại của các giỏ tăng dần theo vị trí từ đầu nhịp ra điểm giữa. Giỏ treo tại vị trí giữa nhịp có biên độ dao động cực đại lớn nhất, sau đó giảm dần đến vị trí cuối nhịp.

3.7.3. Sự ảnh hưởng của lực căng ngang H đến biên độ cực đại của dao động giỏ đựng thanh long

Lực căng ngang H sẽ ảnh hưởng nhiều đến vị trí các điểm dây treo giỏ vào cáp, đó là các điểm Ak trong sơ đồ phân tích lực hình 2.9, điều đó sẽ dẫn đến: H sẽ có ảnh hưởng đến biên độ của dao động ngang giỏ. Để khảo sát sự ảnh hưởng của các lực căng ngang đến biên độ cực đại của các dao động giỏ hàng, ta xét biên độ cực đại của giỏ được treo ở một số vị trí trên nhịp cáp.

Kết quả khảo sát ảnh hưởng của lực căng ngang H, đến biên độ cực đại của dao động giỏ đựng thanh long được thể hiện trên hình 3.12 và bảng 3.11

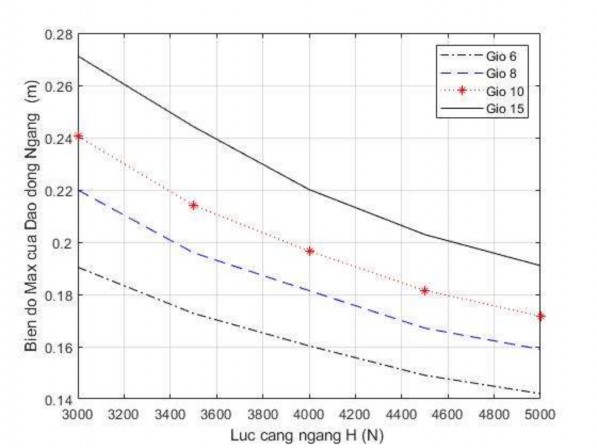
Hình 3.12. Đồ thị biên độ dao động cực đại của giỏ treo ứng với các lực căng ngang khác nhau, với độ dài r = 0,3 m, = 2400 cm

Bảng 3.11. Biên độ dao động cực đại (m) của giỏ ứng với các giá trị H

TT

Lực căng ngang H (N)	Giỏ số 6	Giỏ số 8	Giỏ số 10	Giỏ số 15
1	3000	0.190	0.220	0.241	0.271
2	3500	0.173	0.196	0.214	0.244
3	4000	0.160	0.181	0.197	0.220
4	4500	0.149	0.167	0.182	0.203
5	5000	0.142	0.159	0.172	0.191

Nhận xét:

+ Từ kết quả tính toán cho ta thấy, khi lực căng ngang tăng lên thì biên độ dao động cực đại của giỏ giảm đi.

+ Với lực căng ngang thay đổi trong khoảng 3000 – 5000 N thì biên độ cực đại của giỏ tại giữa nhịp thay đổi trong khoảng 19 – 27 cm.