định. Để các giỏ đựng trái thanh long chuyển động được trên dây cáp thì các giỏ được liên kết lại với nhau bằng sợi dây, khi kéo sợi dây với vận tốc thì toàn bộ giỏ đựng trái thanh long chuyển động theo. Để xác định biên độ dao động của giỏ ta gắn đầu đo gia tốc vào giỏ đựng trái thanh long sao cho phương cần đo trùng với phương dao động.
Sau khi công tác lắp đặt được hoàn tất, sử dụng pa lăng xích để căng dây cáp, khi căng dây cáp đến một giá trị nhất, màn hình máy tính hiển thị giá trị lực căng. Sau đó dùng tời để kéo giỏ đựng trái thanh long chuyển động với vận tốc nhất định, cảm biến đo gia tốc ghi lại gia tốc của đường cáp, đầu đo lực xác định lực căng dây cáp, sử dụng máy đo thủy bình để xác định độ vòng của đường dây cáp.
Tiếp tục kéo palăng để tăng lực kéo, tiếp tục cho giỏ đựng trái thanh long chuyển động, thiết bị đo ghi lại được lực căng, dao động; Sử dụng máy thủy bình xác định được độ vòng ứng với lực căng.
Thí nghiệm với sự thay đổi chiều dài nhịp được tiến hành như sau: Dịch chuyển trụ đỡ trung gian theo đúng với khoảng cách nhịp bố trí thí nghiệm. Quá trình tăng lực căng ngang và do độ vòng, và dao động tương tự như phần trên.
Quá trình bố trí thí nghiệm và tổ chức thí nghiệm được thể hiện trên hình 4.7; 4.8.
Hình 4.7. Bố trí thí nghiệm đo lực căng ngang và độ vòng đường cáp
Hình 4.8. Quá trình đo độ vòng và lực căng dây cáp và biên độ dao động của giỏ đựng thanh long
4.6.2. Kết quả đo lực căng, độ vòng của dây cáp và biên độ dao động giỏ đựng trái thanh long
Kết quả đo lực căng dây cáp, độ vòng dây cáp, dao động của giỏ đựng trái thanh long được thể hiện trên hình 4.9, hình 4.10, sau khi xử lý số liệu kết quả được ghi ở bảng 4.1; 4.2; 4.3.
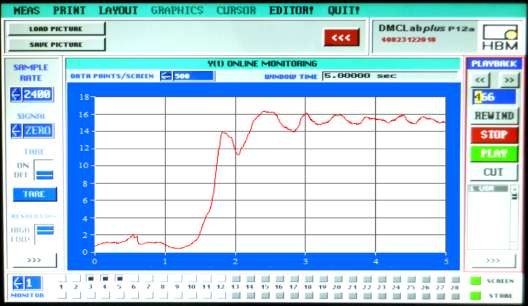
Hình 4.9. Kết quả đo lực căng dây cáp
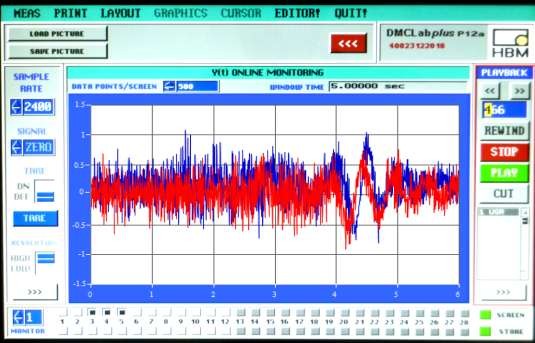
Hình 4.10. Kết quả đo gia tốc của giỏ đựng trái thanh long
4.7. So sánh kết quả nghiên cứu lý thuyết với kết quả thực nghiệm
Sau khi có kết quả thực nghiệm, luận án tiến hành so sánh kết quả thực nghiệm với kết quả tính theo lý thuyết, quá trình so sánh trong cùng điều kiện, kết quả so sánh được thể hiện như sau:
4.7.1. So sánh ảnh hưởng của chiều dài nhịp đến độ vòng đường cáp trong trường hợp không tải
Để đánh giá mức độ tin cây của mô hình tính toán lý thuyết, luận án tiến hành so sánh kết quả khảo sát theo mô hình lý thuyết đã lập ở chương 2 với kết quả thực nghiệm thu được, kết quả so sánh được thể hiện trên bảng 4.1.
Bảng 4.1. Kết quả so sánh ảnh hưởng của chiều dài nhịp và lực căng ngang đến độ vòng lớn nhất của đường cáp
Chiều dài nhịp (cm) | Độ vòng max f (cm) | Sai số (%) | ||
Lý thuyết | Kết quả thực nghiệm | |||
3000 | 2000 | 33.0 | 30.0 | 9.1 |
5000 | 2000 | 20.0 | 22.0 | 10.2 |
3000 | 2800 | 65.0 | 67.4 | 3.7 |
5000 | 2800 | 39.0 | 40.4 | 3.7 |
3000 | 2400 | 48.0 | 46.6 | 2.9 |
5000 | 2400 | 29.0 | 29.2 | 0.6 |
4000 | 2000 | 25.0 | 23.0 | 8.1 |
4000 | 2800 | 49.0 | 50.9 | 3.8 |
4000 | 2400 | 36.0 | 34.9 | 3.2 |
Có thể bạn quan tâm!
-
Vùng Tần Số Cộng Hưởng Dao Động Ngang, Dọc Của Giỏ Trên Nhịp -
Sự Ảnh Hưởng Của Độ Dài Nhịp Cáp Đến Biên Độ Cực Đại Của Dao Động Giỏ Đựng Thanh Long -
Phương Pháp Xác Định Các Đại Lượng Nghiên Cứu Và Thiết Bị Đo -
Ảnh Hưởng Của Chiều Dài Nhịp Đến Độ Vòng Của Đường Dây Cáp. -
Đồ Thị Độ Biên Độ Dao Động Cực Đại Của Giỏ Phụ Thuộc H Và Nhận Xét: Với Các Hàm Hồi Quy Nhận Được Là Hàm Phi Tuyến, Từ Hàm Hồi Qui -
Nghiên cứu động lực học đường cáp vận chuyển trái thanh long ở vùng Tây Nam Bộ - 20
Xem toàn bộ 196 trang tài liệu này.
Nhận xét:Kết quả tính theo công thức lý thuyết và kết quả thực nghiệm có sai số lớn nhất < 11% là có thể chấp nhận được, như vậy mô hình tính toán lý thuyết và mô hình thí nghiệm là có thể tin cậy được.
4.7.2. So sánh dao động của đường cáp
Sau khi thu được kết quả nghiên cứu thực nghiệm khi xác định được các giá trị gia tốc ta sử dụng phần mềm Dasylab tích phân hai lần xác định được biên độ dao động, luận án tiến hành so sánh với kết quả khảo sát lý thuyết, kết quả so sánh
được thể hiện bảng 4.2 và bảng 4.3.
Bảng 4.2. Kết quả so sánh ảnh hưởng của chiều dài nhịp và lực căng ngang đến biên độ dao động
Chiều dài nhịp (m) | Biên độ dao động a (cm) | Sai số (%) | ||
Lý thuyết | Kết quả thực nghiệm | |||
3000 | 2000 | 21.0 | 23.9 | 13.6 |
5000 | 2000 | 15.6 | 17.0 | 8.7 |
3000 | 2800 | 35.0 | 35.9 | 2.4 |
5000 | 2800 | 23.1 | 26.3 | 13.8 |
3000 | 2400 | 27.5 | 30.6 | 11.4 |
5000 | 2400 | 19.8 | 22.4 | 13.2 |
4000 | 2000 | 17.9 | 18.9 | 5.3 |
4000 | 2800 | 27.5 | 29.5 | 7.3 |
4000 | 2400 | 22.0 | 25.0 | 13.5 |
Bảng 4.3. Ảnh hưởng của lực căng đường cáp đến độ vòng khi chiều dài nhịp
=2200 cm và tải trọng phân bố đều q = 0,2 N/cm
Lực căng ngang H (N) | Độ vòng lớn nhất f (cm) | |||||||
Lần 1 | Lần 2 | Lần 3 | Trung bình | Kết quả thực nghiệm | Lý thuyết | Sai số % | ||
1 | 3000 | 42 | 40 | 44 | 42.0 | 41.8 | 40.3 | 4 |
2 | 3500 | 30 | 33 | 34 | 32.3 | 32.6 | 34.6 | 6 |
3 | 4000 | 25 | 27 | 26 | 26.0 | 26.4 | 30.3 | 13 |
4 | 4500 | 23 | 24 | 25 | 24.0 | 23.1 | 26.9 | 14 |
5 | 5000 | 22 | 21 | 24 | 22.3 | 22.7 | 24.2 | 6 |
Nhận xét: kết quả tính theo công thực lý thuyết và kết quả thực nghiện có sai số lớn nhất là 14 % vẫn có thể chấp nhận được vì hệ thống không yêu cầu độ chính xác cao, như vậy mô hình tính toán lý thuyết là có thể tin cậy được.
4.8. Xác định một số thông số hợp lý của đường cáp vận chuyển trái thanh long
4.8.1. Kết quả thực nghiệm đơn yếu tố
4.8.1.1. Ảnh hưởng của lực căng dây cáp đến độ vòng của đường cáp
a) Kết quả thí nghiệm
Đề tài đã tiến hành thí nghiệm: Cố định chiều dài nhịp cáp = 2200 cm tải trọng q=0,2 N/cm, thay đổi lực căng dây cáp H1 =3000N; H2 = 3500N;
H3 =4000N; H4= 4500N; H5 =5000N. Kết quả thí nghiệm đo độ vòng được ghi ở bảng 4.3.
b) Thiết lập phương trình tương quan
Thiết lập phương trình tương quan dạng bậc 2:
f = a0 + a1H + a2H2
Từ số liệu thực nghiệm trên bảng 4.3, bằng phương pháp bình phương nhỏ nhất, dẫn đếna = (a0 , a1. a2) sẽ là nghiệm của hệ phương trình đại số :
5a 2 104 a 825 105 a
146,7
0 1 2
2a 8250 a 35 106 a
56,28
(4.8)
0 1 2
825a 35 105a 152213105a 22344,2
0 1 2
Giải ra ta được giá trị các hệ số của hàm hồi quy :
- Mô hình hồi quy: f = 157,5 -0,056. H + 5,810-6. H2 (4.9)
Để kiểm tra tính đồng nhất của phương sai và tính tương thích của mô hình, lập bảng với số thí nghiệm n = 5 , số lần thí nghiệm lặp r =3, số các hệ số cần xác định ( trừ hệ số a0) : m = 2.
Trung bình | Hồi quy | Si2 | Sia2 | |
1 | 42.0 | 41.8 | 4.00 | 0.05 |
2 | 32.3 | 32.6 | 4.33 | 0.10 |
3 | 26.0 | 26.4 | 1.00 | 0.18 |
4 | 24.0 | 23.1 | 1.00 | 0.78 |
5 | 22.3 | 22.7 | 2.33 | 0.14 |
S2 = | 12.67 | Sa2 = 1.26 | ||
Max (Si2) = | 4.33 |
2 S2
12,67
2 S 2
1,26
Có Sts 2,53 ; Sdu a 0,628
n 5 n m 1 2
Max( S 2 )
4,33
S 2 2,53
Gtt i 0.342 ; Ftt ts 4,03 ,
S
du
S 2 12,67 2 0,628
Lấy mức độ chính xác của nghiên cứu = 0,05
- Kiểm tra tính đồng nhất của phương sai:
Tra bảng phân vị Cochran C(r-1, n ,1-) = C(2 , 5 , 0.95) = 0,6638
=> Gb = 0,6638. Có Gtt = 0,342 < Gb = 0,6638 => Phương sai của thí nghiệm được coi là đồng nhất.
- Kiểm tra tính tương thích của phương trình hồi quy:
Tra bảng Fisher : F(n-m-1 , n(r-1), 1- ) = F(2 , 10 , 0.95) = 4,103
=> Fb = 4,103. Có Ftt = 4,03 < Fb = 4,103 => mô hình hồi quy là tương thích Từ kết quả thí nghiệm ở bảng 4.3 ta xây dựng được đồ thị tương quan giữa
lực căng dây cáp với độ vòng lớn nhất như hình 4.11.
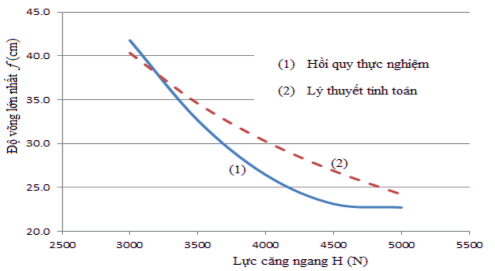
Hình 4.11. Đồ thị tương quan giữa độ vòng lớn nhất và lực căng ngang của dây cáp
4.8.1.2. Ảnh hưởng của lực căng dây cáp đến biên độ dao động của giỏ đựng thanh long
a) Kết quả thí nghiệm
Đề tài đã tiến hành thí nghiệm: Cố định chiều dài nhịp là 2400 cm; tải trọng q
= 0,2 N/cm, thay đổi lực căng dây cáp H1 =3000N; H2 = 3500N; H3 =4000N; H4= 4500N; H5 = 5000N. Kết quả thí nghiệm đo dao động được ghi ở bảng 4.4.
Bảng 4.4. Ảnh hưởng của lực căng ngang đường cáp đến biên độ dao động cực đại của giỏ ở giữa nhịp
( chiều dài nhịp = 2400 cm và tải trọng phân bố đều q = 0.2 N/cm)
Lực căng ngang H (N) | Biên độ lớn nhất tại giữa nhịp (cm) | |||||||
Lần 1 | Lần 2 | Lần 3 | Trung bình | Hồi quy thực nghiệm | Lý thuyết | Sai số % | ||
1 | 3000 | 29 | 30 | 29 | 29,3 | 29,5 | 26,0 | 13 |
2 | 3500 | 25 | 26 | 25 | 25,3 | 24,8 | 23,0 | 8 |
3 | 4000 | 20 | 22 | 21 | 21,0 | 21,4 | 21,0 | 2 |
4 | 4500 | 18 | 21 | 19 | 19,3 | 19,2 | 20,0 | 4 |
5 | 5000 | 18 | 19 | 18 | 18,3 | 18,3 | 19,5 | 6 |
b) Thiết lập phương trình tương quan
Thiết lập phương trình tương quan dạng bậc 2 với A là biên độ dao động cực đại của giỏ.
A = a0 + a1H + a2H2
Từ số liệu thực nghiệm trên bảng 4.4, bằng phương pháp bình phương nhỏ nhất, dẫn đếna = (a0 , a1. a2) sẽ là nghiệm của hệ phương trình đại số :
5a 2 104 a 825 105 a
113,3
0 1 2
2a 8250 a 35 106 a
43,9
(4.10)
0 1 2
0 1 2
825a 35 105a 152213105a
17601,6
Giải ra ta được giá trị các hệ số của hàm hồi quy :
- Mô hình hồi quy: A = 83,4 - 0,0254 H + 2,476 10-6. H2 (4.11)
Để kiểm tra tính đồng nhất của phương sai và tính tương thích của mô hình, lập bảng với số thí nghiệm n = 5 , số lần thí nghiệm lặp r =3, số các hệ số cần xác định (trừ hệ số a0) : m = 2 ở bảng sau:
Trung bình | Hồi quy | Si2 | Sia2 | |
1 | 29,3 | 29,5 | 0,33 | 0,03 |
2 | 25,3 | 24,8 | 0,33 | 0,24 |
3 | 21,0 | 21,4 | 1,00 | 0,18 |
4 | 19,3 | 19,2 | 2,33 | 0,01 |
5 | 18,3 | 18,3 | 0,33 | 0,00 |
S2 = | 4,33 | Sa2 = 0,46 | ||
Max (Si2) = | 2,33 |
2 S 2
4,33
2 S 2
0,46
Có Sts 0.87 ; Sdu a 0,228
n 5 n m 1 2
Max( S 2 )
2,33
S 2 0,87
Gtt i 0,538 ; Ftt ts 3,8 ,
S
du
S 2 4,33 2 0,228
Lấy mức độ chính xác của nghiên cứu = 0,05
- Kiểm tra tính đồng nhất của phương sai:
Tra bảng phân vị Cochran C(r-1, n ,1-) = C(2 , 5 , 0.95) = 0,6638
=> Gb = 0,6638. Có Gtt = 0,538 < Gb = 0,6638 => Phương sai của thí nghiệm được coi là đồng nhất.
- Kiểm tra tính tương thích của phương trình hồi quy:
Tra bảng Fisher : F(n-m-1 , n(r-1), 1- ) = F(2 , 10 , 0.95) = 4,103
=> Fb = 4,103. Có Ftt = 3,8 < Fb = 4,103 => mô hình hồi quy là tương thích Từ kết quả thí nghiệm ở bảng 4.4 ta xây dựng được đồ thị tương quan giữa lực
căng dây cáp với biên độ dao động lớn nhất của giỏ tại vị trí giữa nhịp như hình 4.12.
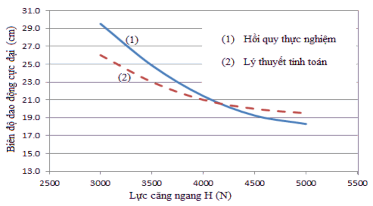
Hình 4.12. Đồ thị tương quan giữa với biên độ dao động cực đại của giỏ đựng thanh long ở giữa nhịp cáp với lực căng ngang