Các Mô Hình Phân Tích Và Dự Báo Vỡ Nợ Của Khách Hàng Cá Nhân

2.3. Thiết kế nghiên cứu

2.3.1. Mẫu nghiên cứu

Dữ liệu nghiên cứu được thu thập từ nguồn dữ liệu của Ngân hàng HTX Việt Nam. Dữ liệu quá khứ về việc vỡ nợ hay không vỡ nợ của các KHCN tại ngân hàng sẽ được sử dụng (khách hàng là những cá nhân vay vốn phục vụ mục đích kinh doanh cá nhân hoặc hộ gia đình). Mẫu nghiên cứu thu được 5.498 khách hàng tại Ngân hàng HTX Việt Nam. Với số lượng mẫu 5.498, đảm bảo tin cậy về số lượng mẫu tối thiểu và tính đại diện khi phân tích dữ liệu đa biến (Hoàng Trọng và Chu Nguyễn Mộng Ngọc, 2008).

2.3.2. Thu thập dữ liệu

Với các biến nghiên cứu được xác định trong mô hình nghiên cứu, tác giả tiến hành gửi tới bộ phận phụ trách khách hàng tại Hội sở của Ngân hàng HTX Việt Nam để xin dữ liệu thông tin tình hình trả nợ của KHCN. Thông tin khách hàng về họ tên, số điện thoại và địa chỉ không được đưa vào dữ liệu phân tích. Các thông tin được cung cấp hoàn toàn bảo mật và chỉ sử dụng cho nghiên cứu này của tác giả. Mỗi chi nhánh được NCS thu thập khoảng từ 100 - 500 khách hàng.

2.4. Phương pháp phân tích dữ liệu

2.4.1. Mô tả dữ liệu

Mẫu thu thập được tiến hành phân loại theo các nhóm được định sẵn bằng các kỹ thuật thống kê mô tả hay tính tần suất.

Trung bình mẫu (mean) trong thống kê là một đại lượng mô tả thống kê, được tính ra bằng cách lấy tổng giá trị của toàn bộ các quan sát trong tập chia cho số lượng các quan sát trong tập.

Có thể bạn quan tâm!

• Hoạt Động Xếp Hạng Tín Dụng Trong Các Ngân Hàng
• Hệ Thống Ký Hiệu Xếp Hạng Tín Dụng Khách Hàng Cá Nhân Tại Bidv
• Những Yếu Tố Ảnh Hưởng Đến Xác Suất Vỡ Nợ Của Khách Hàng Cá Nhân
• Hoạt Động Sử Dụng Vốn Của Ngân Hàng Hợp Tác Xã Việt Nam
• Kết Quả Phân Tích Các Yếu Tố Ảnh Hưởng Lên Khả Năng Vỡ Nợ Của Khcn
• Kết Quả Trọng Số Mô Hình Phân Loại Rừng Ngẫu Nhiên (Random Forest)

Xem toàn bộ 136 trang tài liệu này.

Các biến nghiên cứu là biến định danh hoặc thứ bậc sẽ được tác giả thực hiện tính toán tần suất để so sánh tỉ lệ phần trăm. Đồng thời, sử dụng bảng so sánh chéo crosstab để đánh giá về quan hệ các yếu tố nhân khẩu học ở dạng thống kê (chủ yếu tập trung quanh giới tính).

2.4.2. Phân tích tương quan

Do đặc thù biến phụ thuộc là biến định danh hay nhị phân chỉ nhận giá trị 1 và 0 nên khi đó hệ số tương quan sẽ không còn ý nghĩa (do hệ số tương quan giữa các biến r tính toán dựa trên cả giá trị độ lệch chuẩn, với biến định danh và thứ bậc thì yếu tố độ lệch chuẩn không có ý nghĩa). Đồng thời, các biến độc lập trong mô hình cũng gồm nhiều biến phân loại nên chỉ số hệ số tương quan sẽ không có ý nghĩa khi so sánh tương quan giữa các biến độc lập. Do vậy, trong phần trình bày kết quả nghiên cứu, tác giả sẽ không đưa ma trận hệ số tương quan giữa các biến và biến phụ thuộc vào.

2.4.3. Các mô hình phân tích và dự báo vỡ nợ của khách hàng cá nhân

2.4.3.1. Mô hình Logit

Với đặc trưng của biến phụ thuộc là vỡ nợ của khách hàng được đo lường bằng 1 nếu vỡ nợ (không trả được nợ) và là 0 nếu không vỡ nợ (trả được nợ). Do đó, mô hình hồi quy Logistic sẽ được sử dụng để phân tích các yếu tố ảnh hưởng lên khả năng vỡ nợ của KHCN.

Hồi quy Logistic là mô hình hồi quy đặc biệt khi biến phụ thuộc là một biến nhị phân chỉ nhận hai giá trị 0 và 1. Mô hình hồi quy này sử dụng để dự đoán xác suất xảy ra một sự việc dựa vào thông tin các biến độc lập trong mô hình.

Xác suất: Là khả năng để sự việc xảy ra, ký hiệu là P

Odds là tỷ lệ so sánh giữa hai xác suất: Xảy ra sự việc và không xảy ra.

Khi chúng ta có biến phụ thuộc chỉ có hai lựa chọn: Y = 1, Y = 0 và xác suất để sự việc đó xảy ra ký hiệu là P (Y = 1) = P. Các nhà thống kê thường sử dụng một đại lượng quen thuộc là Odds của sự việc xảy ra, chứ không phải là xác suất để sự việc đó xảy ra và Odds được tính như sau:

Odds 

P

1P

Như vậy, theo công thức này thì Odds là một hàm số theo P. Odss >= 0 và Odds sẽ không xác định khi P = 1.

Từ công thức trên, ta có:

P Odds Odds 1

Như vậy, xác suất P là một hàm số theo Odds.

Ta có P là xác suất xảy ra sự kiện thì (1 – P) là xác suất không xảy ra sự kiện, xác suất P được đo lường như sau:

Pi 

1

1 eZi

1

1e( 0 1 X1 2 X 2 ...k X k )

Với

Z 0 1 X1 2 X2 ...k Xk

Zi (, ) ,

Pi (0,1) Xi (i 1,k)

P 1eziz

Odds của 2 trường hợp trên là: Odds ie i

z

1Pi 1e i

Lấy Log cơ số e của Odds ta có dạng hàm mô hình hồi quy Logit:

i

L  ln( Pi

) Z X X  ... X

1Pi

i 0 1 1 2 2 k k

Với

Xi (i 1,k) : Là các biến độc lập

(i) Tác động biên của biến thứ k

Ý nghĩa: Khi thay đổi Xk một đơn vị thì xác suất để cho Y = 1 (cũng chính là Pi) sẽ thay đổi Pi.(1 - Pi). k. Sự thay đổi xác suất theo giải thích này phụ thuộc vào hai yếu tố. Yếu tố thứ nhất là dấu của hệ số k. Nếu hệ số mang dấu (+) thì có nghĩa là

khi tăng biến Xk sẽ tác động làm tăng xác suất cho Y = 1 và ngược lại. Yếu tố thứ hai là sự thay đổi xác suất cho Y = 1 khi thay đổi Xk sẽ lại phụ thuộc vào giá trị cụ thể của Xk, có nghĩa là việc tăng (giảm) xác suất Pi khi thay đổi Xk sẽ không cố định mà nó sẽ thay đổi tương ứng với giá trị của biến Xk và sự thay đổi này nằm trong phạm vi của

điều kiện cơ bản của xác suất là 0 Pi  1

(ii). Mối quan hệ giữa tác động biên của xác suất biến phụ thuộc tăng lên từ P0 lên P1 khi thay đổi một đơn vị của Xk :

Odds0

P0

1 p0

ez0

Trong đó, P0 là xác suất khởi điểm:

Z0 1 2 X2i ... k Xki

Odds1

P1

1p1

ez1

Trong đó, P1 là xác suất khi Xk tăng thêm một đơn vị

Z1 1 2 X 2i  ... k ( X ki 1)

Từ 2 phương trình trên ta có:

O1ekO O ek(1)

O

1 0

0

P P O ek

Thay Odds 1vào (1)

1 O ekp  0

1 1p

1p 0 1 1O ek

1 1 0

Từ mối quan hệ này chúng ta có thể xây dựng kịch bản cho sự thay đổi của xác suất khi thay đổi một đơn vị của biến Xk, sự thay đổi này bằng cách quan sát chênh lệch của P0 và P1, chúng ta lấy P1- P0 sẽ tìm ra sự thay đổi của xác suất khi thay đổi một đơn vị của Xk. Ưu điểm của cách mô phỏng này cho chúng ta thấy được sự thay đổi xác suất cụ thể, còn cách lý giải tác động biên về xác suất ở phần trước chỉ mang tính định tính.

Kiểm định mô hình hồi quy

Độ phù hợp của mô hình: Chúng ta dựa vào chỉ tiêu LL (log likelihood), thước đo này có ý nghĩa giống như SSE (Sum of squares of error) nghĩa là có giá trị càng nhỏ càng tốt. Giá trị nhỏ nhất của LL là 0 (tức là không có sai số) khi đó mô hình có một độ phù hợp hoàn hảo.

Ngoài ra chúng ta còn có thể dựa vào bảng dự báo theo các mức xác suất chuẩn C tùy thích bằng SPSS để xác định mô hình dự đoán tốt đến đâu. Đây là bảng so sánh trị số thực và trị số dự đoán cho từng biểu hiện và tính tỷ lệ dự đoán đúng sự kiện. Với giá trị khả năng dự báo trên 50% sẽ được coi là phù hợp.

Kiểm định ý nghĩa của các hệ số: Hồi quy Logit sử dụng đại lượng Wald Chi square để kiểm định ý nghĩa thống kê của hệ số hồi quy tổng thể. Wald Chi square được tính bằng cách lấy ước lượng của hệ số hồi quy của biến độc lập trong mô hình (hệ số hồi quy mẫu) Logit chia cho sai số chuẩn của ước lượng hệ số hồi quy này sau đó lấy bình phương như sau:

2 

B 2 

Wald.Chi square s.e.() 

s.e.(B) 



Kiểm định độ phù hợp tổng quát: Trong hồi quy Logit, tổ hợp liên hệ tuyến tính của toàn bộ các hệ số trong mô hình ngoại trừ hằng số cũng được kiểm định xem có thực sự có ý nghĩa trong việc giải thích cho biến phụ thuộc không. Với hồi quy tuyến tính bội

ta dùng thống kê F để kiểm định giả thuyết:

H0 : 1 2  ... 3  0 . Tuy nhiên, trong

hồi quy Logit ta sử dụng kiểm định khi - bình phương. Với mức p-value< 0.05 ta bác bỏ giả thuyết H0, chấp nhận giả thuyết H1 tức là các hệ số hồi quy khác nhau có ý nghĩa thống kê và các hệ số đều thực sự có ý nghĩa trong việc giải thích biến phụ thuộc.

2.4.3.2. Mô hình Probit

Hồi quy Probit: Trong hồi quy Probit, tích lũy tiêu chuẩn hàm phân phối chuẩn Φ(⋅) được sử dụng để mô hình hàm hồi quy khi biến phụ thuộc là nhị phân, nghĩa là chúng ta giả sử:

E(Y|X)=P(Y=1|X)=Φ(β0+β1X) (*)

β0+β1Xβ0+β1X trong(*) đóng vai trò là một phân vị z:

Φ(z)=P(Z≤z) , Z∼N(0,1)

Như vậy mà hệ số Probit β1trong (*) là thay đổi trong Z được liên kết với thay đổi một đơn vị trong X. Mặc dù ảnh hưởng đến Z của một sự thay đổi trong X là tuyến tính, liên kết giữa Z và biến phụ thuộc Y là phi tuyến từ Φ là hàm phi tuyến của X.

Do biến phụ thuộc là hàm phi tuyến của các biến hồi quy, nên hệ số trên X không giải thích đơn giản. Sự thay đổi dự kiến trong xác suất Y = 1 do sự thay đổi trong P /I có thể được tính như sau:

Tính xác suất dự đoán rằng Y =1 cho giá trị ban đầu của X. Tính xác suất dự đoán rằng Y = 1 cho X + ∆ X

Tính toán sự khác biệt giữa cả hai xác suất dự đoán.

Tất nhiên chúng ta có thể khái quát hóa (*) thành hồi quy Probit với nhiều biến hồi quy để giảm thiểu rủi ro đối mặt với sai lệch biến bị bỏ qua.

2.4.3.3. Mô hình phân tích biệt số/phân biệt

Mô hình phân tích biệt số có dạng tuyến tính như sau:

=++++ ⋯ +

Trong đó:

D: Biệt số

b: Hệ số hay trọng số phân biệt Xi: Biến độc lập

Các hệ số hay trọng số (bi) được tính toán sao cho các nhóm có các giá trị của hàm phân biệt (biệt số D) khác nhau càng nhiều càng tốt. Điều này sẽ xảy ra khi tỷ lệ của tổng các độ lệch bình phương của biệt số giữa các nhóm so với tổng các độ lệch bình phương của biệt số trong nội bộ các nhóm đạt cực đại. Hàm phân biệt này lần lượt được ước lượng, xác định mức ý nghĩa và tính toán điểm phân biệt (cutting point).

Tuy nhiên, mô hình phân tích biệt số chỉ phân tích cho các biến số độc lập là các biến định lượng (thang đo khoảng, thang đo tỷ lệ). Trong mô hình nghiên cứu của tác giả, tồn tại cả các biến độc lập là định tính và định lượng nên mô hình phân tích biệt số không phù hợp trong trường hợp nghiên cứu này.

2.4.3.4. Mô hình dự báo mạng Neuron nhân tạo (ANN)

Mô hình dự báo phá sản sử dụng mạng Neuron nhân tạo được thực hiện từ những năm 80 khi có sự phát triển mạnh mẽ của máy tính cũng như công cụ toán (Gouvêa & Bacconi, 2007). Bên cạnh các mô hình dự báo như mô hình Logistic, mô hình phân tích biệt số được sử dụng khi ANN vượt qua các ràng buộc về thống kê (Atiya, 2001; du Jardin, 2010). Sự phát triển của thuật toán lan truyền ngược (backpropagation) là bước ngoặt cho sự phổ biến của các mạng thần kinh (Fausett, 1994). ANN chủ yếu sử dụng trong dự báo, phân loại trong kinh tế và tài chính. Việc cải thiện khả năng dự báo là quan trọng trong việc đánh giá khả năng phá sản của cá nhân hay doanh nghiệp (Keasey &Watson, 1987; Ohlson, 1980). Do đó, việc tạo ra mô hình vượt qua các ràng buộc để mang lại kết quả dự báo tốt nhất như ANN là điều cần thiết (Jardin, 2010).

Mạng Neuron nhân tạo xuất phát từ tiếng Anh là Arificaial Neural Network và ký hiệu là ANN. Là một dạng mô hình có thể xử lý thông tin mô phỏng dựa trên hoạt động của hệ thống thần kinh. Tại đó, việc xử lý thông tin dựa trên các Neuron. Việc thực hiện mô phỏng dựa trên huấn luyện như não người. Các kinh nghiệm cùng khả năng lưu trữ kinh nghiệm này sẽ được đúc rút đưa ra các trọng số tiên đoán cho tương lai.

PE

PE

PE

PE

PE

PE

PE

PE

Output layer

Hidden layer

Trong mô hình phân tích này khi sử dụng mạng ANN, các lớp đầu vào là 20 biến độc lập có khả năng tác động lên khả năng vỡ nợ của khách hàng. Để có thể đưa ra các hệ số hay trọng số cho từng biến thì cần có giả định cho các lớp ẩn (hidden layer) để xử lý các thông tin. Sau khi xử lý thông tin qua các hidden layer thì sẽ tới lớp đầu ra là biến phụ thuộc là biến về vỡ nợ của KHCN. Với số lượng biến đầu vào là 20 chưa phải là số lượng lớn, nên NCS sẽ không sử dụng hidden layer để trực tiếp đưa ra hệ số hay trọng số của từng biến mà không cần qua bước trung gian phân tích. Quy trình phân tích được thể hiện qua hình sau:

Input layer

Hình 2.2. Mô hình ANN

Processing Elements (PE): Các PE của ANN gọi là Neuron, mỗi Neuron nhận các dữ liệu vào (Inputs) xử lý chúng và cho ra một kết quả (output) duy nhất. Kết quả xử lý của một Neuron có thể làm Input cho các Neuron khác.

Trong đó các tín hiệu hay nhận đầu vào (input) là các biến độc lập tương ứng với đó là các trọng số gắn với các biến độc lập để dự báo cho biến đầu ra (output layer). Biến đầu ra output layer có thể có từ 1 đến nhiều biến đầu ra. Thông tin từ input layer đến output layer được truyền và xử lý qua hiddent layer. Một mô hình có thể sử dụng 0 hoặc nhiều hidden layer. Weights (trọng số liên kết): Đây là thành phần rất quan trọng của một ANN, nó thể hiện mức độ quan trọng (độ mạnh) của dữ liệu đầu vào đối với quá trình xử lý thông tin (quá trình chuyển đổi dữ liệu từ layer này sang layer khác). Quá trình học (Learning Processing) của ANN thực ra là quá trình điều chỉnh các trọng số (Weight) của các input data để có được kết quả mong muốn.

Tính tổng trọng số của tất cả các input được đưa vào mỗi Neuron (phần tử xử lý PE). Hàm tổng của một Neuron đối với n input được tính theo công thức sau:

=

Mục tiêu của ANN là tìm ra các trọng số W để đưa ra mối quan hệ giữa các biến độc lập và biến phụ thuộc về vỡ nợ của các KHCN tại các ngân hàng.

2.4.3.5. Mô hình dự báo bằng Random Forest

Random Forest (RF) là một dạng mô hình phân lớp dữ liệu được sử dụng rộng rãi trong những năm gần đây (phương pháp ước lượng Random Forest xuất hiện từ 1995 do Ho đưa ra và sau đó được Breiman phát triển thêm vào năm 2010). Random = Tính ngẫu nhiên; Forest = Nhiều cây quyết định (decision tree) là một trong những thuật toán về cây quyết định, trong quá trình xây dựng cây RF chọn ngẫu nhiên các quan sát (observations) quá trình này gọi là bootstrapping và chọn ngẫu nhiên các thuộc tính quá trình này gọi là attribute sampling. Random Forest được đánh giá cao bởi tính chính xác của mô hình (Booth et al., 2014; Breiman, 2001; Ho, 1995). Nhược điểm chính của Random Forest là khối lượng tính toán lớn tuy nhiên với năng lực tính toán ngày càng tăng của máy tính (theo cấp lũy thừa) thì hạn chế của Random Forest không phải là vấn đề lớn. Quy trình của RF được mô tả như sau:

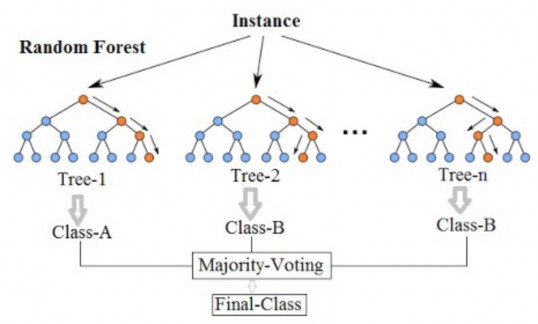
Hình 2.3. Mô hình Random Forest

Xem tất cả 136 trang.