TN1 | Ngân hàng A có nhiều hoạt động đóng góp cho xã hội (học bổng, quỹ từ thiện…). | |
TN2 | Ngân hàng A rất quan tâm đến vấn đề bảo vệ môi trường. | |
Uy tín ngân hàng | ||
Karatepe và ctg (2005); Stubbs và Cocklin (2007); Pina & ctg (2009), Bravo & ctg (2012) | UT1 | Ngân hàng A có lịch sử hình thành và phát triển lâu đời. |
UT2 | Ngân hàng A có danh tiếng tốt trên thị trường. | |
Mạng lưới chi nhánh | ||
Stubbs và Cocklin (2007) | ML1 | Ngân hàng A có nhiều chi nhánh, phòng giao dịch |
Pina & ctg (2009); Bravo & ctg (2012) | ML2 | Chi nhánh ngân hàng A gần nhà hoặc nơi làm việc của tôi. |
ML3 | Phòng giao dịch của ngân hàng A thoải mái, bày trí đẹp mắt. | |
Nhân sự | ||
Stubbs và Cocklin (2007) | NS1 | Tôi không phải chờ lâu khi giao dịch với ngân hàng A |
Pina & ctg (2009); Bravo & ctg (2012) | NS2 | Nhân viên ngân hàng A luôn thân thiện, cởi mở. |
NS3 | Nhân viên ngân hàng A có tác phong chuyên nghiệp. | |
NS4 | Nhân viên ngân hàng A luôn quan tâm đến quyền lợi của khách hàng. |
Có thể bạn quan tâm!
-
Đề Xuất Mô Hình Định Giá Thương Hiệu Nhtm Việt Nam -
Cơ Sở Lý Thuyết Về “Tài Sản Thương Hiệu” (Brand Equity- Cbbe) -
Đề Xuất Mô Hình “Tài Sản Thương Hiệu” Của Nhtm Việt Nam -
Vai Trò Của Hệ Số Beta Trong Qui Trình Định Giá Thương Hiệu -
Quy Trình Nghiên Cứu Định Lượng Dựa Trên Số Liệu Sơ Cấp -
Mô Hình Đo Lường Tài Sản Thương Hiệu Nhtm Việt Nam Theo Cbbe.
Xem toàn bộ 187 trang tài liệu này.
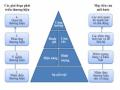
Bảng 2.6 Thang đo “Nhận biết về thương hiệu” (Brand Awareness)
Ký hiệu | Thang đo | |
Nhận diên thương hiệu | ||
NB1 | Tôi nhận ra logo của ngân hàng A khi thấy logo xuất hiện ở bất cứ đâu | |
Yoo và Donthu (2001). | ||
NB2 | Tôi dễ dàng nhận ra chi nhánh ngân hàng A, trong số các ngân hàng khác |
NB3 | Tôi nhận thấy chi nhánh ngân hàng A khác biệt, đẹp mắt hơn so với ngân hàng khác | |
Hồi tưởng thương hiệu | ||
Yoo. & Donthu (2001). | NB4 | Tôi có thể nhanh chóng nhớ được Logo hay các biểu tượng của ngân hàng A |
NB5 | Tôi dễ dàng liên tưởng đến thương hiệu ngân hàng A trong tâm trí của mình. |
Bảng 2.7 Thang đo “Sự tin tưởng vào thương hiệu” (Brand trust)
Ký hiệu | Thang đo | |
Sự tin tưởng | ||
Delgado-Ballester (2004) | TT1 | Thông tin quảng cáo của ngân hàng A là trung thực, đáng tin cậy. |
Erdem and Swait (2004) | TT2 | Tôi tin rằng ngân hàng A sẽ giải quyết được những khó khăn tài chính của tôi. |
TT3 | Tôi tin rằng ngân hàng A sẽ bồi thường thiệt hại cho tôi nếu có. | |
TT4 | Tôi cảm thấy yên tâm khi sử dụng dịch vụ của ngân hàng A | |
TT5 | Qua kinh nghiệm giao dịch với ngân hàng A, tôi tin rằng ngân hàng A luôn thực hiện các cam kết với khách hàng. |
Bảng 2.8 Thang đo “Mối quan hệ ngân hàng-khách hàng” (Relationship)
Ký hiệu | Thang đo | |
Lobschat & ctg (2013); Fischer & ctg (2010); | RE1 | Là một khách hàng thân thiết lâu năm, Tôi nhận được từ ngân hàng A những dịch vụ mà các khách hàng khác không được nhận |
Vogel & ctg (2008) | RE2 | Tôi quen thuộc với các nhân viên giao dịch trong ngân hàng A |
RE3 | Tôi thấy vui vẻ khi gặp các khách hàng khác tại ngân hàng A. | |
RE4 | Nhân viên ngân hàng A biết tên tôi. | |
RE5 | Tôi có niềm tin vào thương hiệu ACB |
Bảng 2.9 Thang đo “Tài sản thương hiệu” (Brand Equity)
Ký hiệu | Thang đo | |
BE1 | Tôi có thể mong đợi ngân hàng A luôn cung cấp những dịch vụ tốt nhất | |
Vogel & ctg (2008) | BE2 | Nếu các ngân hàng khác có dịch vụ tương tự, tôi vẫn chọn ngân hàng A |
BE3 | Lựa chọn ngân hàng A là hợp lý, dù cho các ngân hàng khác có dịch vụ tương tự |
Luận án dựa vào các nghiên cứu về “Tài sản thương hiệu” và thực hiện nghiên cứu định lượng để xác định các thành phần của tài sản thương hiệu NHTM Việt Nam và tỉ trọng đóng góp của các thành phần vào tài sản thương hiệu. Từ đó xác định “Chỉ số vai trò thương hiệu” theo các thông số tìm được từ kết quả nghiên cứu.
2.4 Cơ sở lý thuyết về hệ số Beta thị trường có điều chỉnh đòn bẩy trong mô hình định giá thương hiệu NHTM Việt Nam
2.4.1 Các nghiên cứu thực nghiệm về hệ số beta thị trường có điều chỉnh đòn bẩy (Proxy Levered Beta - PLB)
Mô hình CAPM (Sharpe, 1964)
Mô hình CAPM do Sharpe đề xuất năm 1964, được xây dựng trên nền tảng lý thuyết danh mục của Markowitz (1952) nhưng có bổ sung một số giả định quan trọng (phụ lục). Nghiên cứu độc lập của Lintner (1965), Mossin (1966) cũng đạt kết quả tương tự. Mô hình CAPM thể hiện một cách rõ ràng mối quan hệ giữa rủi ro hệ thống và tỉ suất sinh lợi (TSSL) kỳ vọng của một tài sản, theo công thức:
Re = E(Ri) = Rf + βi[E(Rm) – Rf] (1)
Trong đó, E(Ri) là TSSL kỳ vọng của tài sản i, E(Rm) là TSSL kỳ vọng thị trường, Rf là TSSL phi rủi ro, βi là Beta của tài sản i, [E(Rm) – Rf] là phần bù rủi ro thị trường.
Mối quan hệ này được diễn tả bằng đường thị trường chứng khoán (SML). (Hình 2.7)
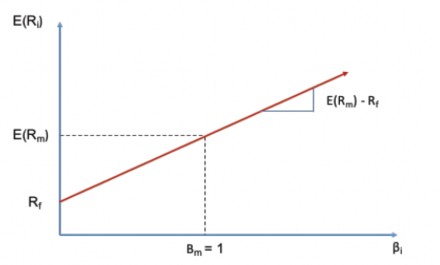
Hình 2.9 Đường thị trường chứng khoán (SML).
Nguồn: Sharpe (1964)
Beta trong mô hình CAPM là hệ số phản ánh mối quan hệ giữa độ biến động của giá chứng khoán i với sự biến động của mức giá chung trên thị trường, được xác định bằng công thức:
(2)
Với Corr(Ri, Rm) đại diện cho tương quan giữa tỷ suất sinh lợi của tài sản i với thị trường; σi và σm là độ lệch chuẩn của tài sản và thị trường.
Hiệp phương sai (Covariance) là thước đo xu hướng thay đổi của hai đối tượng Ri và Rm với nhau. Tuy nhiên, nhà đầu tư không thể dựa vào hiệp phương sai để kết luận xu hướng mạnh hay yếu của hai yếu tố với nhau. Vì vậy, để khắc phục vấn đề này, hiệp phương sai sẽ được chia cho số nhân hai độ lệch chuẩn và được gọi là hệ số tương quan. Khi đó, công thức về Beta có thể viết lại như sau:
βi = Cov(Ri,Rm) / σ2m (3)
Trong đó, Cov(Ri,Rm) là hiệp phương sai giữa TSSL chứng khoán i và TSSL thị trường, σ2m là hiệp phương sai của thị trường với chính nó.
Như vậy, để tính toán beta đòi hỏi chứng khoán i phải được niêm yết. Beta của các chứng khoán đã niêm yết được xác định theo công thức này được gọi là beta dựa trên thị trường (Market Based Beta, MBB hoặc βm).
Đo lường rủi ro hệ thống
Mô hình CAPM thể hiện mối quan hệ giữa rủi ro hệ thống và tỉ suất sinh lợi kỳ vọng của tài sản. Vì vậy, rủi ro hệ thống được đo lường thông qua tỷ suất sinh lợi kỳ vọng, thể hiện qua phương sai hay độ lệch chuẩn đại diện cho mức độ rủi của một tài sản cụ thể so với một tài sản trung bình.
Tỷ suất sinh lợi của một tài sản (cổ phiếu) khi tính toán theo công thức:
R = E(R) + U (4)
Trong đó, R là tỷ suất sinh lợi thực tế hay tổng tỷ suất sinh lợi (total return); E(R) là tỷ suất sinh lợi kỳ vọng (expected return); và U đại diện cho tỷ suất sinh lợi ngoài kỳ vọng (unexpected return).
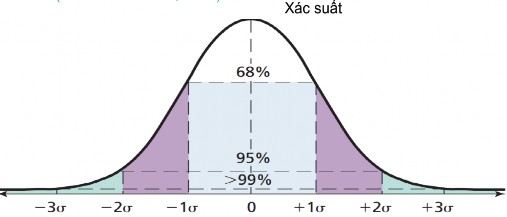
Để đo lường rủi ro bằng phương sai và độ lệch chuẩn, Jordan & Miller Jr (2009) dùng khái niệm phân phối chuẩn (normal distribution), còn được gọi là biểu đồ hình chuông (bell curve), dùng để mô tả xác suất xuất hiện của tỷ suất sinh lợi thực tế trong một phạm vi cho trước. Phân phối này hoàn toàn được mô tả bởi giá trị trung bình và độ lệch chuẩn. Nếu phân phối tần suất của tỷ suất sinh lợi thực tế cũng có dạng biểu đồ hình chuông hoặc gần giống với phân phối chuẩn thì xác suất để một tỷ suất sinh lợi thực tế xuất hiện trong khoảng từ giá trị tỷ suất sinh lợi trung bình cộng trừ một khoảng bằng một lần độ lệch chuẩn là 68%, hai lần độ lệch chuẩn là 95% (hình 3.1).
Hình 2.10 Phân phối chuẩn.
Nguồn : Jordan & Miller Jr (2009)
Qua phân tích ở trên ta thấy chỉ có rủi ro hệ thống có ảnh hưởng đến phần bù rủi ro và tỷ suất sinh lợi kỳ vọng, E(R), nên nên việc đo lường rủi ro hệ thống tương ứng với mỗi tài sản luôn được nhà đầu tư và thẩm định viên quan tâm. Hệ số beta (β) được sử dụng để đại diện cho loại rủi ro này (Jordan & Miller Jr, 2009). Theo đó, beta là hệ số phản ánh rủi ro hệ thống tương đối của một tài sản cụ thể so với một tài sản trung bình. Beta càng cao thì độ nhạy cảm với thị trường càng mạnh và có rủi ro hệ thống càng lớn. Độ nhạy cảm này phụ thuộc vào hai yếu tố: (i) mức độ tương quan giữa tỷ suất sinh lợi của tài sản (Ri) với tỷ suất sinh lợi thị trường (Rm); (ii) độ biến động của tài sản đó so với thị trường.
Hệ số Beta thị trường có điều chỉnh đòn bẩy (Beta bottom-up hay Proxy Levered Beta, PLB)
Hamada (1972) đã phát triển cách xác định hệ số Beta dựa trên mối quan hệ giữa đòn bẩy tài chính và rủi ro hệ thống. Sau đó, Rubinstein (1973) tiếp tục mở rộng mô hình này bằng cách kết hợp tác động của thuế suất thuế thu nhập doanh nghiệp (τ) với giá trị thị trường của nợ (D) trong việc ước tính beta không đòn bẩy, theo công thức:
(5)
Trong đó, βuMM là beta không đòn bẩy (Proxy Unlevered Beta, PUB), βm là beta thị trường của doanh nghiệp, D/E là tỷ số nợ trên vốn chủ sở hữu và τ là thuế suất thuế thu nhập doanh nghiệp.
Lý thuyết về đòn bẩy tài chính của Modigliani & Miller (1963) cho rằng giá trị doanh nghiệp sẽ tăng lên cùng với đòn bẩy tài chính trong môi trường có thuế thu nhập doanh nghiệp. Tuy nhiên, nếu một doanh nghiệp sử dụng nợ vay quá cao sẽ tiềm ẩn rủi ro về nguy cơ phá sản khi hoạt động không hiệu quả. Vì vậy, Myers (1977) đã mở rộng lý thuyết trên với sự hiện diện của chi phí khánh kiệt tài chính và các chi phí liên quan đến phá sản và được gọi là lý thuyết đánh đổi (trade-off theory). Theo lý thuyết đánh đổi, để tối ưu hiệu quả hoạt động, doanh nghiệp phải lựa chọn một cấu trúc vốn vừa có vốn vay vừa có vốn cổ phần, với mức vay nợ tối ưu khi lợi ích cận biên của tấm chắn thuế bằng với chi phí cận biên của rủi ro phá sản. Mối quan hệ
giữa đòn bẩy tài chính và rủi ro hệ thống được đề cập cụ thể trong nghiên cứu của Hamada (1972), khẳng định vai trò của đòn bẩy tài chính trong việc tính toán rủi ro hệ thống và phát triển thành beta không đòn bẩy. Mô hình nghiên cứu này được nhiều học giả tập trung phát triển (Rubinstein, 1973; Bowman, 1979; Gahlon & ctg, 1982; Mandelker & ctg, 1984; Fernandez, 2006; Guthrie, 2011). Tại Việt Nam, kết quả nghiên cứu của Nguyễn Kim Đức & ctg (2015) đối với 167 doanh nghiệp trên sàn HoSE giai đoạn 2006-2014 cũng cho thấy tồn tại mối quan hệ có ý nghĩa thống kê giữa đòn bẩy tài chính và rủi ro hệ thống.
Hệ số Beta có điều chỉnh đòn bẩy (Proxy Levered Beta, PLB) được ước tính lại dựa trên hệ số PUB bình quân, bằng cách sử dụng hệ số đòn bẩy tài chính D/E riêng biệt của doanh nghiệp cần định giá hay doanh nghiệp chưa niêm yết (Bowman & ctg, 2006) và phương pháp này được gọi là Beta Bottom-up (Damodaran, 2002).
PLB = PUBAV * ⌊𝟏 + 𝐃 (𝟏 − 𝐭)⌋ (6)
𝐄
Trong đó, PLB là Beta có đòn bẩy tài chính, PUBAV là Beta bình quân, D/E là hệ số đòn bẩy tài chính của doanh nghiệp cần định giá, t là thuế suất thuế thu nhập doanh nghiệp.
Đòn bẩy tài chính và rủi ro hệ thống của NHTM
Đòn bẩy tài chính (Financial Leverage, FL) sử dụng chi phí tài chính cố định làm điểm tựa. Đòn bẩy tài chính có thể được thể hiện qua các tỷ số như: (i) tỷ số tổng nợ vay trên tổng tài sản (Thompson, 1976); (ii) tỷ số tổng nợ trên tổng vốn cổ phần (Hamada, 1972); (iii) tổng nợ vay, tổng nợ ngắn hạn, tổng nợ dài hạn trên tổng tài sản (Frank & ctg, 2009; Pandey, 2011).
Khi doanh nghiệp sử dụng chi phí tài chính cố định, một thay đổi trong lợi nhuận trước thuế và lãi (EBIT) sẽ trở thành một thay đổi tương đối lớn trong lợi nhuận sau thuế (EAT). Tác động số nhân của việc sử dụng các chi phí tài chính cố định được gọi là độ nghiêng đòn bẩy tài chính (Degree of Financial Leverage, DFL).
Việc sử dụng đòn bẩy tài chính sẽ tạo nên rủi ro tài chính, là tính khả biến tăng thêm của lợi nhuận tính trên 1 cổ phiếu (EPS) hay xác suất mất chi trả khi doanh nghiệp sử dụng các nguồn tài trợ có chi phí cố định.
Cấu trúc đòn bẩy tài chính của các NHTM rất lớn và khá biến động. Cách tiếp cận bottom-up (Damodaran, 2002) được đề xuất để ước tính hệ số Beta cho các NHTM trong nghiên cứu này. Nền tảng của cách tiếp cận bottom-up được dựa trên nguyên lý rủi ro hệ thống và phụ thuộc vào ba yếu tố: (i) lĩnh vực kinh doanh; (ii) đòn bẩy tài chính; và (iii) đòn bẩy kinh doanh.
Vì ngân hàng chỉ có một lĩnh vực kinh doanh là tiền tệ, khác với các doanh nghiệp kinh doanh đa ngành nên khi ước tính hệ số Beta sẽ không xét đến yếu tố lĩnh vực kinh doanh. Mặt khác, ngành ngân hàng là ngành kinh doanh đặc biệt, cung cấp dịch vụ tài chính ngân hàng, liên quan đến một loại hàng hóa đặc biệt là “tiền tệ”, nên đòn bẩy kinh doanh (mối quan hệ giữa định phí và biến phí) của ngân hàng có cơ cấu khá ổn định, nên ngân hàng khó chủ động điều chỉnh đòn bẩy kinh doanh như doanh nghiệp. Trong khi đó, đòn bẩy tài chính là yếu tố quan trọng trong cơ cấu vốn của ngân hàng. Beta có điều chỉnh đòn bẩy (Proxy Levered Beta) có nhiều ưu điểm và phù hợp để ước lượng rủi ro thị trường của NHTM thông qua Beta. Ý tưởng cách tiếp cận Bottom-up xuất hiện từ khi có các nghiên cứu về mối quan hệ giữa đòn bẩy hoạt động, đòn bẩy tài chính và rủi ro hệ thống được thực hiện (Sabogal & ctg, 2014). Mặt khác, ở góc độ nghiên cứu trực tiếp về ước tính hệ số beta, các nghiên cứu tập trung chủ yếu vào beta của các doanh nghiệp và ngân hàng đã niêm yết thông qua tính ổn định của hệ số này (Gooding & ctg, 1977; Faff, 2001). Với các doanh nghiệp chưa niêm yết, hoặc vừa niêm yết, hoặc đã niêm yết nhưng vừa tái cấu trúc đòn bẩy, khi việc ước tính beta còn gặp nhiều khó khăn (Renzi & ctg, 2013). Khi đó, hệ số beta có điều chỉnh đòn bẩy (PLB) được đề xuất như một giải pháp ưu việt vì vừa thể hiện được đầy đủ rủi ro hệ thống của doanh nghiệp, vừa có thể ước tính được Beta của doanh nghiệp chưa có cổ phiếu niêm yết (Beneda, 2003; Renzi & ctg, 2013; Nguyen & ctg, 2018).