Phép Quay Quanh Tâm Là Điểm Bất Kì. (A) Đối Tượng Trước Khi Biến Đổi,(B) Sau Khi Tịnh Tiến Về Gốc Tọa Độ, (C) Sau Khi Quay Góc Α, (D) Sau Khi Tịnh

1 0 0

1 1

Sx



0 0



Sx



1  1 1

MS 

Sx.Sy

 0

 0

Sy 0

0 1

 0



 0



0

Sy 

0 1



MS (Sx , Sy )

Ma trận phép biến đổi ngược của phép Quay góc 

R

M 1 

cos



sin

 sin0 cos

M R

()

0



 0 0 1

4.5. Kết hợp các phép biến đổi

Quá trình áp dụng các phép biến đổi liên tiếp để tạo nên một phép biến đổi tổng thể được gọi là sự kết hợp các phép biến đổi (composing transformation).

Giả sử điểm P(x,y) bị biến đổi qua n phép biến đổi T1, T2,…, Tn với các ma trận biến đổi tương ứng M1, M2, ..., Mn(n>0) thành điểm P‘(x‘,y‘). Khi đó công thức biến đổi tổng hợp là: P‘= P*M

Trong đó M = M1*M2*…*Mn gọi là ma trận biến đổi tổng hợp.

Nghĩa là thực hiện từ n phép biến đổi trở lên là thực hiện phép nhân ma trận có n ma trận. Chú ý: Vì phép nhân ma trận không có tính chất giao hoán nên thứ tự các phép biến đổi thường không thể đảo.

4.5.1. Kết hợp các phép tịnh tiến

Thực hiện tịnh tiến điểm X(x,y) theo vector (Tx1,Ty1) được X‘(x‘,y‘), tiếp tục tịnh tiến điểm P‘(x‘,y‘) theo vector (Tx2,Ty2) được X‖(x‖,y‖)

Hai ma trận biến đổi tương ứng:

1



T1  0

0 0



1 0

1



T2  0

0 0



1 0

Tx Ty 1Tx Ty 1

1 1 2 2 

Công thức biến đổi:

X‘ = X*T1 ; X‖ = X‘*T2 X‖ = X*T1*T2

Hay ma trận biến đổi tổng hợp M = T1*T2

M =

1 0 0

0 1 0 ∗

𝑇𝑥1 𝑇𝑦1 1

1 0 0

0 1 0

𝑇𝑥2 𝑇𝑥2 1

1 0 0

= 0 1 0

𝑇𝑥1 + 𝑇𝑥2 𝑇𝑦1 + 𝑇𝑦2 1

Nhận xét: Kết hợp 2 phép tịnh tiến được một phép tịnh tiến => Kết hợp nhiều phép tịnh tiến được 1 phép tịnh tiến.

M = T1*T2*...+ Tn =

1 0 0

0 1 0

𝑇𝑥1 + 𝑇𝑥2 + ⋯ + 𝑇𝑥𝑛 𝑇𝑦1 + 𝑇𝑦2 + ⋯ + 𝑇𝑦𝑛 1

Ví dụ: Cho tứ giác ABCD với: A(3,3), B(5,2), C(6,5), D(2,5). Xác định tọa độ mới của tứ giác sau khi tính tiến tứ giác sao cho trọng tâm trùng với điểm Q(8,8) rồi tịnh tiến tiếp theo vector tịnh tiến (2, 2).

Tứ giác ABCD với: A(3,3), B(5,2), C(6,5), D(2,5) có trọng tâm G(4,4) Dịch chuyển tứ giác sao cho trọng tâm trùng với điểm Q(8,8) :



8  4 dx dx  4



( dx, dy là khoảng dịch chuyển theo trục x;y)

8  4 dy dy  4

1 0 0



T10 1 0

4 4 1

- Tịnh tiến tứ giác theo vector tịnh tiến (2, 2):

- Công thức biến đổi tổng hợp:

1 0 0



T 20 1 0

2 2 1

X'X*T1*T2x y

1 0 01 0 0



1* 0 1 0* 0 1 0



1 0 0

4 4 12 2 1

= x y

1* 0 1 0(x  6) ( y  6) 1

6 6 1

y ' y  6

x ' x  6



Áp dụng : A(3,3) A‘(9,9)

B(5,2) B‘(11,8)

C(6,5) C‘(12,11)

D(2,5) D‘(8,11)

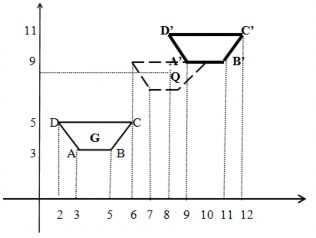
Hình 4.7. Ví dụ phép tịnh tiến

4.5.2. Kết hợp các phép tỉ lệ

Thực hiện co giãn điểm X(x,y) theo vector (Sx1 ,Sy1) được X‘(x‘,y‘), tiếp tục co giãn điểm P‘(x‘,y‘) theo vector (Sx2,Sy2) được X‖(x‖,y‖)

Hai ma trận biến đổi tương ứng:

1

Sx



0 0



Sx

2



0 0





S1  0

 0

Sy1 0

1

0





S2  0



 0

Sy2 0

1

0





Công thức biến đổi:

X‘ = X*S1 ; X‖ = X‘*S2 X‖ = X*S1*S2

Hay ma trận biến đổi tổng hợp M = S1*S2

𝑆𝑥1

0	0 𝑆𝑥2	0	0 𝑆𝑥1 ∗ 𝑆𝑥2	0	0
M = 0	𝑆𝑦1	0 ∗ 0	𝑆𝑦2	0 = 0	𝑆𝑦1 ∗ 𝑆𝑦2	0
0	0	1 0	0	1 0	0	1

Có thể bạn quan tâm!

• Các Trường Hợp Xén Tỉa Một Cạnh Của Cửa Sổ Với Biên Cửa Sổ
• Đồ họa máy tính - 12
• Phương Pháp Biểu Diễn Đối Tượng Trong Không Gian Hai Chiều
• Xây Dựng Công Thức Biến Đổi Đối Tượng Khi Thực Hiện Các Phép Biến Đổi:
• Đồ họa máy tính - 16
• Vật Thể Ba Chiều Được Biểu Diễn Bằng Mô Hình Khung Nối Kết

Xem toàn bộ 240 trang tài liệu này.

Nhận xét: Kết hợp hai phép co giãn là một phép co giãn => Kết hợp nhiều phép co giãn cũng là một phép co giãn

M = S1*S2*...+ Sn =

𝑆𝑥1 ∗ 𝑆𝑥2 ∗ … ∗ 𝑆𝑥1 0 0 0 𝑆𝑥𝑦1 ∗ 𝑆𝑥𝑦2 ∗ … ∗ 𝑆𝑦𝑛 0

0 0 1

Ví dụ: Cho  ABC với: A(3,4), B(5,4) C(2,3). Xác định tọa độ mới của  sau khi thực hiện phóng to tam giác lên gấp 2 lần, sau đó tiếp tục thực hiện phép tỉ lệ với hệ số Sx=Sy=-1;

Bước 1: Phóng to tam giác lên gấp 2 lần  thực hiện phép tỉ lệ với hệ số Sx= Sy = 2

2 0 0



Ma trận biến đổi: T10 2 0

0 0 1

Bước 2: phép tỉ lệ với hệ số Sx=Sy=-1

1 0 0

Ma trận biến đổi: T 2 0 1 0



 0 0 1

+ Công thức biến đổi tổng hợp:

2 0 01 0 0

[X‘]=[X]*[T1]*[T2] = x y

1* 0 2 0* 0 1 0



2 0 0

0 0 1 0 0 1

= x y 1* 0 2 0



 0 0 1

y ' 2 y

x ' 2x



+ Áp dụng:

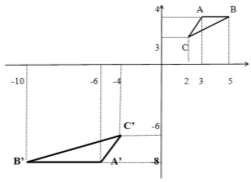
Hình 4.8. Ví dụ về phép tỉ lệ

A (3,4) A‘(-6,-8)

B(5,4) B‘(-10,-8)

C(2,3) C‘(-4,-6)

4.5.3. Kết hợp các phép quay

Thực hiện quay điểm X(x,y) theo góc 1 được X‘(x‘,y‘), tiếp tục quay điểm X‘(x‘,y‘) theo góc 2 được X‖(x‖,y‖)

Hai ma trận biến đổi tương ứng:

cos α1 sin α1 0 cos α 2 sin α2 0

R1 = − sin α 1 cos α 1 0 R2 = − sin α2 cos α2 0

0 0 1

Công thức biến đổi:

X‘ = X*R1 ; X‖ = X‘*R2 X‖ = X*R1*R2

Hay ma trận biến đổi tổng hợp M = R1*R2

0 0 1

cos α1 sin α1 0 cos α 2 sin α2 0

M = − sin α 1 cos α 1 0 − sin α2 cos α2 0

0 0 1 0 0 1

cos α1 + α2

sin α1 + α2	0
= −sin α1 + α2	cos α1 + α2	0
0	0	1

Nhận xét: Kết hợp hai phép quay là một phép quay => Kết hợp nhiều phép quay cũng là một phép quay

4.5.4. Phép quay có tâm quay là điểm bất kỳ

Giả sử tâm quay có tọa độ (xf , yf), khi đó phép quay được đưa về trường hợp quay quanh gốc tọa độ theo các bước:

- Tịnh tiến đối tượng theo vector tịnh tiến (-xf, -yf) để dịch chuyển tâm quay về gốc tọa độ

- Thực hiện quay theo góc α cho trước

- Tịnh tiến ngược đối tượng theo vector tịnh tiến (xf , yf) để dịch chuyển tâm quay về vị trí ban đầu.

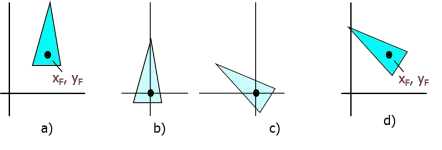
Hình 4.9. Phép quay quanh tâm là điểm bất kì. (a) Đối tượng trước khi biến đổi,(b) Sau khi tịnh tiến về gốc tọa độ, (c) Sau khi quay góc α, (d) Sau khi tịnh tiến

về tâm quay ban đầu.

Ma trận phép biến đổi

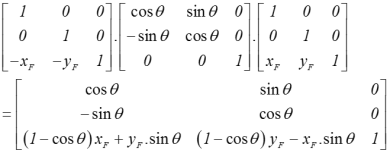
4.5.5. Phép tỉ lệ giữ nguyên điểm chốt

Thực hiện phép tỉ lệ với hệ số tỉ lệ (Sx, Sy) sao cho điểm chốt (x0, y0) không đổi

Các bước thực hiện

- Dịch đối tượng sao cho điểm chốt trùng gốc tọa độ

- Thực hiện co dãn theo tỷ lệ cho trước

- Dịch ngược đối tượng sao cho điểm chốt về vị trí ban đầu

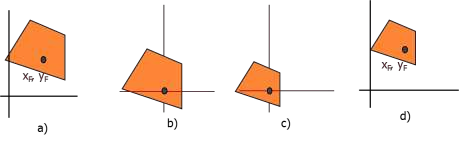
Hình 4.10. Phép tỉ lệ giữ nguyên điểm chốt

Bước 1: Phép tịnh tiến tỉ lệ đến gốc tọa độ có ma trận là:

1	0	0
T1=	0	1	0

−𝑥0 −𝑦0 1

Bước 2: Phép tỉ lệ với hệ số tỉ lệ (Sx, Sy)

𝑆𝑥

0	0
T2= 0	𝑆𝑦	0
0	0	1

Bước 3: Phép tịnh tiến tỉ lệ về vị trí ban đầu có ma trận là

1

0	0
T3= 0	1	0
𝑥0	𝑦0	1

Bước 4: Ma trận của phép tỉ lệ với hệ số tỉ lệ (Sx,Sy) giữ nguyên điểm chốt (x0, y0) được thực hiện bởi tích của 3 phép biến đổi sau:

T=T1*T2*T3

1	0	0 𝑆𝑥	0	0 1	0	0
=	0	1	0 ∗ 0	𝑆𝑦	0 ∗ 0	1	0

−𝑥0 −𝑦0 1

0 0 1

𝑥0 𝑦0 1

𝑆𝑥	0	0
𝑥0 ∗ (1 − 𝑆𝑥 )	𝑦0 ∗ (1 − 𝑆𝑦 )	1

= 0 𝑆𝑦 0

4.6. Phép biến đổi giữa các hệ tọa độ

Để thuận tiện cho việc mô tả đối tượng, thông thường đối tượng sẽ được mô tả trong các hệ tọa độ cục bộ gắn với chúng. Tuy nhiên để có thể hiển thị toàn bộ một ảnh bao gồm nhiều đối tượng thành phần, các mô tả này phải được chuyển về một hệ tọa độ chung duy nhất. Việc chuyển đổi này thường được chia làm hai loại : chuyển từ các hệ tọa độ không phải là hệ tọa độ Descartes như hệ tọa độ cực, hệ tọa độ cầu, hệ tọa độ elliptic, … sang hệ tọa độ Descartes, và chuyển đổi giữa hai hệ tọa độ Descartes. Trong phần này chúng ta sẽ khảo sát phép biến đổi giữa hai hệ tọa độ Descartes với nhau.

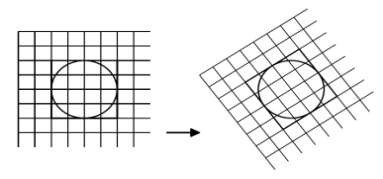
Hình 4.11. Phép biến đổi giữa hai hệ tọa độ

Giả sử ta có hệ tọa độ (I) có gốc tọa độ O và các vector đơn vị lần lượt là i, j. Hệ tọa độ (II) là ảnh của hệ tọa độ (I) qua phép biến đổi T(M), có gốc tọa độ là O‘ và các vector đơn vị lần lượt là u,v. Lúc này một điểm P(x,y) bất kì trong hệ tọa độ (I) sẽ được biến đổi thành điểm Q(a,b) trong hệ tọa độ (II). Vấn đề đặt ra ở đây là mối liên hệ giữa a,b với x, y, M như thế nào

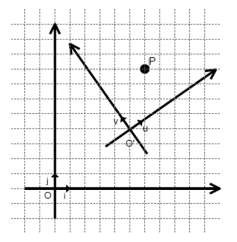
Hình 4.12. Tọa độ của một điểm qua phépbiến đổi hệ tọa độ

Người ta chứng minh được rằng Q=PM-1