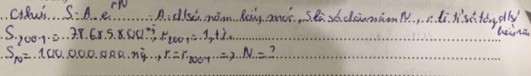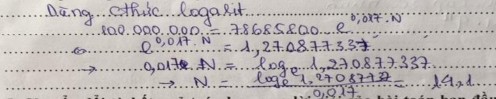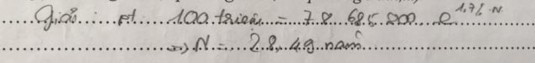TL
Hoạt động của HS | Hoạt động của GV | Nội dung | |
H: Làm thế nào để giải được phương trình ax b ? Gợi ý: - Có nhận xét gì về số nghiệm của phương trình khi b 0? b>0? - Vẽ đồ thị hàm số y ax và đường thẳng y = b trong cùng 1 hệ trục tọa độ ứng với các trường hợp b 0? b>0, từ đó quan sát số giao điểm của 2 đồ thị. - Với b>0, viết b dưới dạng lũy thừa cơ số a? - Tìm x? H: Vận dụng cách giải phương trình mũ để xác định số năm cần tìm. | (1,084)n 2 n= log1,084 2 8,59 Vì số năm là số tự nhiên nên số năm cần tìm là 9 năm. | ||
8’ | VD2. Một người gửi ngân hàng 100 triệu đồng theo thể thức lãi kép định kì liên tục, với lãi suất r% mỗi năm. Sau 5 năm thì thu được cả vốn lẫn lãi là 200 triệu đồng. Hỏi sau bao lâu người đó gửi 100 triệu ban đầu mà thu được 400 triệu đồng cả vốn lẫn lãi. | ||
a) + HS tìm hiểu đề bài + HS xác định các thông tin toán học cần thiết. + Xác định chiến lược giải quyết: tính số tiền người đó thu được sau 1 năm, 2 năm, 5 năm năm? + Thiết lập phương trình xác định lãi suất | H: Làm thế nào để xác định được số năm? Gợi ý: - Để xác dịnh được số năm trước hết cần xác dịnh điều gì? - Tính số tiền thu được sau 5 năm theo r. - Giải tìm r. - Tính số tiền thu được sau n năm theo n. - Giải tìm n. | Theo bài ra ta có r5 200 1001 100 r 52 1100. 100152 1100n 400 n 8. | |
Có thể bạn quan tâm!
-
Dạy học toán ở trường THPT theo hướng phát triển năng lực giải quyết vấn đề thực tiễn thông qua việc khai thác và sử dụng các tình huống thực tiễn - 21 -
Sách Giáo Khoa, Sách Bài Tập Đại Số Và Giải Tích -
Ổn Định Tổ Chức: Kiểm Tra Sĩ Số Lớp. -
Dạy học toán ở trường THPT theo hướng phát triển năng lực giải quyết vấn đề thực tiễn thông qua việc khai thác và sử dụng các tình huống thực tiễn - 25 -
Dạy học toán ở trường THPT theo hướng phát triển năng lực giải quyết vấn đề thực tiễn thông qua việc khai thác và sử dụng các tình huống thực tiễn - 26
Xem toàn bộ 214 trang tài liệu này.
TL
Hoạt động của HS | Hoạt động của GV | Nội dung | |
+Tính số tiền người đó thu được sau n năm? + Thiết lập được phương trình + Giải phương trình tìm số năm | |||
Hoạt động 2: Tìm hiểu cách giải một số phương trình mũ đơn giản | |||
10’ | TL: x = y 3 5x7 3 x1 a) 2 2 x 1 b) 32(3x1) 38x2 x 0 c) 2( x2 2) 243x x 1 x 2 | H: So sánh x, y nếu ax a y ? Gọi HS lên bảng trình bày lời giải | 2. Cách giải một số phương trình mũ đơn giản a) Đưa về cùng cơ số: a f (x) ag(x) f (x) g(x) Ví dụ: Giải các phương trình sau 5x7 2 x1 a) (1,5) 3 b) 93x1 38x2 x2 2 c) 1 243x 2 |
8’ | VD3: Bèo hoa dâu được thả nuôi trên mặt nước ngọt tại nhiều vùng quê của Việt Nam, sự phát triển của loài bèo này rất nhanh, cứ sau một tuần bèo phát triển thành 3 lần ban đầu. Loài bèo này cũng rất có hữu ích trong nông nghiệp. Mới đây các nhà khoa học Việt Nam đã phát hiện ra nó có thể được dùng để chiết xuất ra chất có tác dụng kích thích hệ miễn dịch và hỗ trợ điều trị bệnh ung thư. Một người đã thả một lượng bèo hoa dâu chiếm 3% diện tích mặt hồ. Hỏi, sau bao nhiêu ngày bèo sẽ phủ kín 81% mặt hồ? | ||
Sau 1 tuần lượng bèo là: 3%.3 Sau 2 tuần lượng bèo là: 3%.3.3=3%.32 Sau n tuần lượng bèo là: 3%.3n. | H: GV cho HS tính lượng bèo sau 1, 2 tuần từ đó khái quát lên n tuần. | Lượng bèo hoa dâu sau n tuần là: 3%.3n. Để được phủ kín 81% mặt hồ thì 3%.3n 81% 3n 27 33 n 3. Vậy sau 21 ngày lượng bèo sẽ phủ kín 81% mặt hồ. | |
TL
Hoạt động của HS | Hoạt động của GV | Nội dung | |
4' | Hoạt động 3: Củng cố Nhấn mạnh: - Với a > 0, a 1 thì: ax b x loga b - Với a > 0, a 1 thì: a f (x) ag(x) f (x) g(x) Các bước giải bài toán chứa tình huống thực tiễn. | ||
TL
4. BÀI TẬP VỀ NHÀ:
- Bài 1, 2 SGK và các bài tập sau:
1) Sự tăng dân số được ước tính theo công thức
S AerN , trong đó A là dân số của
năm lấy làm mốc tính, S là số dân sau N năm, r là tỉ số tăng dân số hằng năm.
Biết năm 2001, dân số Việt Nam là
S 78.685.800
người và tỉ lệ tăng dân số
năm đó là r 1,7% . Hỏi đến năm nào dân nước ta đạt hơn 100 triệu người, nếu
tỉ số tăng dân số không đổi?
2) Từ ngày 19/6/2012, Ngân hàng Agribank thông báo áp dụng mức lãi suất mới đối với kì hạn 12 tháng gửi bằng VND dành cho khách hàng cá nhân được hưởng mức lãi suất 11%/năm. Giả sử mức lãi suất này không thay đổi và số tiền lãi sau kì hạn lại được cộng vào tiền gốc.
a) Một người gửi tiết kiệm 10 triệu đồng theo kì hạn trên thì sau 5 năm người đó thu về được bao nhiêu tiền cả gốc và lãi?
b) Một người gửi tiết kiệm 10 triệu đồng với kì hạn nêu trên, hỏi sau bao nhiêu năm thì họ được 15 triệu đồng (cả gốc và lãi) ?
3) Một người đem gửi tiết kiệm ở một ngân hàng với lãi suất là 12% năm. Biết rằng cứ sau mỗi một quý (3 tháng) thì lãi sẽ được cộng dồn vào vốn và gốc.
a) Nếu người đó gửi P nghìn đồng thì sau 3 tháng người đó nhận được số tiền (bao gồm cả vốn lẫn lãi) là bao nhiêu ?
b) Hỏi sau tối thiểu bao nhiêu năm thì người đó nhận được số tiền (bao gồm cả vốn lẫn lãi) gấp ba lần số tiền ban đầu ?
- Đọc tiếp bài mục 2 - Một số phương trình mũ đơn giản.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
...................................................................................................................................
PHỤ LỤC VI
CÁC BÀI KIỂM TRA TRƯỚC THỰC NGHIỆM VÀ SAU THỰC NGHIỆM
1. Bài kiểm tra trước TN
a) Yêu cầu kiểm tra
BÀI KIỂM TRA TRƯỚC TN
Bài toán 1: DÂN SỐ
Sự tăng dân số được ước tính theo công thức
S AerN , trong đó A là dân số
của năm lấy làm mốc tính, S là số dân sau N năm, r là tỉ số tăng dân số hằng năm. Biết
năm 2001, dân số Việt Nam là
S 78.685.800
người và tỉ lệ tăng dân số năm đó là
r 1,7% . Hỏi đến năm nào dân số nước ta hơn 100 triệu người, nếu tỉ số tăng dân số không đổi?
HS trả lời theo một số yêu cầu dưới đây:
1) Tìm hiểu vấn đề, thu thập thông tin từ bài toán đã cho
………………………………………………………………………………………
2) Chuyển đổi thông tin từ bài toán đã cho về mô hình TH
………………………………………………………………………………………
3) Sử dụng những kiến thức, kĩ năng để tìm kiếm chiến lược giải quyết mô hình TH
………………………………………………………………………………………
4) Trình bày lời giải bài toán dưới dạng mô hình TH
………………………………………………………………………………………
5) Xem xét, lựa chọn kết quả giải quyết mô hình TH phù hợp với yêu cầu của bài toán ban đầu
………………………………………………………………………………………
Bài toán 2: KINH DOANH NƯỚC MẮM
Để đảm bảo sức khỏe cho người tiêu dùng, Công ty TNHH Daco Việt Nam phối hợp với với Khoa Công nghệ thực phẩm Trường Đại học Nha Trang sản xuất loại mắm “Cá cơm vàng”. Nước mắm được sản xuất theo phương pháp truyền thống hoàn toàn bằng cá cơm, đảm bảo vệ sinh an toàn thực phẩm và 100% không chất bảo quản, đậm đà và thơm. Giá bán hiện nay là 20.000 đồng /chai.
Mỗi tuần Công ty bán được 10.000 chai. Do giá vận chuyển tăng, Công ty có dự kiến tăng giá trong thời gian tới. Qua nghiên cứu thị trường thấy rằng, cứ tăng giá mỗi chai lên
1.000 đồng thì số chai bán được sẽ giảm 100 chai. Em hãy giúp Công ty tính giá bán ra sao cho lợi nhuận cao nhất. Biết chi phí sản xuất mỗi chai nước mắm là 15.000 đồng.
HS trả lời theo một số yêu cầu dưới đây:
1) Tìm hiểu vấn đề, thu thập thông tin từ bài toán đã cho
………………………………………………………………………………………
2) Chuyển đổi thông tin từ bài toán đã cho về mô hình TH
………………………………………………………………………………………
3) Sử dụng những kiến thức, kĩ năng để tìm kiếm chiến lược giải quyết mô hình TH
………………………………………………………………………………………
4) Trình bày lời giải bài toán dưới dạng mô hình TH
………………………………………………………………………………………
5) Xem xét, lựa chọn kết quả giải quyết mô hình TH phù hợp với yêu cầu của bài toán ban đầu
………………………………………………………………………………………
b) Một số thể hiện qua bài làm của HS
Bài toán 1: DÂN SỐ
Số HS | |
Không làm (Có 5 HS không làm bài này, có làm bài toán 2) | 5 |
1) Tìm hiểu vấn đề, thu thập thông tin từ bài toán đã cho HS chỉ ra được các thông tin sau: * Biểu thức S AerN ; S = 100.000 người; A=78.685.800; r 1,7%
| 35 |
Số HS | |
* Số HS xác định thông tin sai | 6 |
2) Chuyển đổi thông tin từ bài toán đã cho về mô hình TH * Giải phương trình mũ sau để xác định N: 100.106 78.685.800.e1,7%. N
| 30 |
* Số HS không xây dựng được, hoặc sai | 5 |
3) Sử dụng những kiến thức, kĩ năng để tìm kiếm chiến lược giải quyết mô hình TH HS lựa chọn phương pháp giải phương trình mũ: 100.106 78.685.800.e0,017. N | 30 |
4) Trình bày lời giải bài toán dưới dạng mô hình TH - Giải toán đúng: 100.106 78.685.800.e0,017. N e0,017.N 1, 27087733 0,017.N ln 1, 27087733 N ln 1, 27087733 14,1 0, 017
| 22 |
* Số lượng HS không giải được, hoặc giải sai: Một số lời giải sai: + 100.106 78.685.800.e1,7%.N N 28, 49
+ 100.106 78.685.800.e1,7%.N N 1, 27 | 8 |
Một số thể hiện cần quan tâm qua bài làm của HS
Số HS | |
+ 100.106 78.685.800.e1,7%. N N 14 | |
5) Xem xét, lựa chọn kết quả giải quyết mô hình TH phù hợp với yêu cầu của bài toán ban đầu * Năm 2016 dân số nước ta đạt 100 triệu người | 8 |
Số HS kết luận sai, hoặc không kết luận được. Một số kết luận sai: * Năm 2015 dân số nước ta đạt 100 triệu người * Năm 2029 dân số nước ta đạt 100 triệu người * Năm 2002 dân số nước ta đạt 100 triệu người | 14 |
Một số thể hiện cần quan tâm qua bài làm của HS
Nhận xét:
- 35 HS thu thập được thông tin liên quan đến vấn đề cần giải quyết.
- 30 HS đã xác định được mô hình TH của bài toán. Tuy nhiên có 5 HS xác định
sai; trong khi đó, bài toán đã nêu rõ công thức tính số dân: S AerN .
- 22 HS đưa về bài toán giải phương trình mũ và giải đúng.