Các Điều Kiện Biên Của Một Vài Dạng Liên Kết

cotg l mc

c EA

Ta dựa vào các ký hiệu = 𝜔 𝑙 𝜀 = 𝑚

𝑐 𝜌𝐴𝑙

Và chú ý đến c2 E , từ phương trình trên ta suy ra



Cotg =  (1.13)

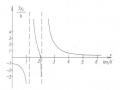
Phương trình đặc trưng (1.13) là một phương trình siêu việt. Giải phương trình này bằng phương pháp số hoặc phương pháp đồ thị (hình 4.3c), ta nhận được một tập vô hạn các giá trị riêng k . Từ đó suy ra các tần số riêng và các hàm riêng

E

l2

c ;

k  1, 2,

k k l k

Xk(x) = Bksink x

l

Nếu ta chọn  = l thì ta có

E

l2

1 = 0,860 c  0,860

1 1 l

E

l2

2 =3,425 c  3, 425

2 2 l

Sơ đồ

Dạng liên kết	Điều kiện đầu
x				Ngàm	u(0,t) = 0
x				Đầu tự do	EA u(0,t)  0 x
x 				Lực dọc	EA u(0,t) N x
 cx l cx				Liên kết đàn hồi tuyến tính	EA u(0,t) cu x EA u(1,t)cu x

Có thể bạn quan tâm!

• Phương Pháp Ma Trận Dạng Riêng (Ma Trận Cản Đặc Biệt)
• A Mô Hình Dao Động Bộ Tắt Chấn Động Lực Có Tính Đến Ma Sát Nhớt
• Dao Động Dọc Tự Do Của Thanh Đồng Chất Tiết Diện Không Đổi
• Thiết Lập Phương Trình Vi Phân Dao Động Uốn Của Dầm
• Dao Động Uốn Tự Do Của Dầm Euler- Bernoulli Đồng Chất Tiết Diện Không Đổi
• Các Phương Trình Đặc Trưng Và Các Trị Riêng Của Một Số Dầm

Xem toàn bộ 182 trang tài liệu này.

	l	m	x x	Đầu lượng	thanh	gắn	khối	u(0,t) 2u EA x m t2
								u(1,t) 2u
								EA x m t2

m

Bảng 4.1 Các điều kiện biên của một vài dạng liên kết

Thí dụ 4.3: Một thanh thẳng bên phải bị ngàm chặt, bên trái gắn vào lò xo như hình 4.4a. Hãy xác định tần số riêng cơ bản khi c*= 2EA/l.

c*

E,A

x

l

c*

N(0,t)

tg







a) b) c)

Hình 4.4 Hình thí dụ 4.3 Lời giải: Các điều kiện biên có dạng

𝜕𝑢 0, 𝑡 𝜔

𝐸𝐴 = 𝑐∗𝑢 0, 𝑡 → 𝐸𝐴𝑋′0 = 𝑐∗𝑋 0 : 𝐸𝐴𝐵 = 𝑐∗𝐴∗

𝜕𝑥 𝑐



u(l,t) =0  X(l) = 0: A* cos c l Bsin

l  0

c

Như thế ta nhận được hệ hai phương trình để xác định A* và B

c* A* 

EA B  0

c

A* cos

l Bsin l  0

l l

Điều kiện cần để A* và B không đồng thời triệt tiêu là định thức hệ số bằng không. Từ đó ta suy ra phương trình đặc trưng

* 

c sin sin l EA cos l  0 tg  0

(1.14)

c c c 2

với  = 𝜔 𝑙

𝑐

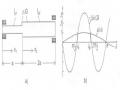
Phương trình đặc trưng (1.14) là phương trình siêu việt. Ta có thể giải phương trình này bằng phương pháp số hoặc phương pháp đồ thị (hình 4.4c). Ta có tần số riêng cơ bản

1 = 2,29 1

= 𝑐 = 2,29

E

l 2

1

𝑙

Chú ý rắng ứng với mỗi k ta có một hàm riêng Xk(x). Nghiệm tổng quát của phương trình (1.3) có dạng

∞

𝑢 𝑥, 𝑡 = 𝑋𝑘 𝑥 𝑇𝑘 𝑡

𝑘=1

Khi xét tới lực cản ngoài tỷ lệ bậc nhất với vận tốc u/t, phương trình vi phân dao động dọc tự do của thanh thẳng đồng chất thiết diện không đổi (1.3) bây giờ có dạng



2u

t2 2

u c

t

2u

2 

x2 0

(1.15)

Trong đó 2δ là hệ số cản.

Áp dụng phương pháp Bernoulli khai triên theo các hàm riêng ta tìm nghiệm phương trình (1.15) dưới dạng

𝑘=1

𝑢 𝑥, 𝑡 = ∞ 𝑇𝑘𝑡 𝑋𝑘𝑥 (1.16)

Trong đó Xk(x) là các hàm riêng, được xác định từ phương trình

d 2 X 2

kK

X K  0

(1.17)

dx2 C 

Thế biểu thức (1.16) vào phương trình (1.15) ta được



[T&&tXx 2T&tXxc2TtX'' (x)]  0

(1.18)

k k k k k

k 1

Chú ý đến 1.17 c2Xk”(x) = - 2kXk(x), phương trình (1.18) có dạng



[T&&t 2T&t2TtX(x)]  0

k k k k k

k 1

Do tính chất của các hàm riêng

1  0 khi k j

X j (x) X k xdx  0

khi k j

0 

Ta suy ra

𝑘

𝑇𝑘𝑡 + 2𝛿𝑇𝑘𝑡 + 𝜔2 𝑇𝑘𝑡 = 0 𝑘 = 1, 2, …. (1.19) Việc tìm nghiệm của phương trình (1.19) đã được xét kỹ trong chương 2. Khi

< k ta có dao động tắt dần

Tk(t) = e-t(Ck cosk*t +Dksink*t ) Trong đó :

𝜔∗ = 𝜔2 − 𝛿2

𝑘 𝑘

Biểu thức nghiêm (1.16) bây giờ có dạng

𝑢 𝑥, 𝑡 = 𝑒−𝛿𝑡∞ (𝐶𝑘 𝑐𝑜𝑠𝜔∗ 𝑡 + 𝐷𝑘 𝑠𝑖𝑛𝜔∗ 𝑡)𝑋𝑘 (𝑥) (1.20)

𝑘=1 𝑘 𝑘

Các hằng số Ck, Dk được xác định từ các điều kiện đầu.

Lực cản trong của thanh là lực cản chiếm ưu thế. Về thực chất loại lực này tuân theo quy luật phi tuyến. Trong phạm vi lý thuyết dao động tuyến tính để đơn giản ta thừa nhận hệ thức

𝐹𝑒𝑡 ~

∂3u

∂x2∂t

Điều đó có nghĩa quan hệ giữa ứng suất biến dạng có dạng

E(u u )

t

Khi đó phương trình dao động dọc tự do của thanh có dạng

(1.21)

2u 

t2

2u

e t

3u



2 i x2t c

2u

2 

x2 0

(1.22)

Trong đó 2e là hệ số cản ngoài, 2i là hệ số cản trong.

4.1.2 Dao động dọc cưỡng bức của thanh thẳng đồng chất tiết diện không đổi

Ở đoạn này ta xét bài toán dao động dọc cưỡng bức của thanh thẳng đồng chất tiết diện không đổi. Để làm thí dụ ta khảo sát dao động của thanh một đầu ngàm, một đầu tự do. Tại đầu tự do tác dụng một lực dọc thay đổi tuần hoàn theo t là F(t)=F0cost (hình 4.5a).









Up(l)

p

U*()

E,A

x

l

a)

1

F0 cost

b)

Hình 4.5 Thanh đồng chất công xon tiết diện không đổi

Phương trình vi phân dao động dọc của thanh

2u 

t2

2

2 u

c x2  0

(1.23)

Các điều kiện bây giờ có dạng

u(0,t) = 0 ; N(l,t) =EAu’(l,t) = F0cost (1.24)

Sự khác nhau giữa bài toán này và bài toán dao động tự do là điều kiện ở biên

tự do. Bài toán này được gọi là bài toán có điều kiện biên không thuần nhất. Nghiệm tổng quát của phương trình vi phân không thuần nhất bao gồm nghiệm tổng quát của phương trình vi phân thuần nhất uh(x,t) và một nghiệm riêng của phương trình vi phân không thuân nhất up(x,t)

u(x,t) = uh (x,t) + up(x, t) (1.25)

Nghiệm tổng quát của bài toán tuyến tính thuần nhất có dạng

𝑘=1

𝑢𝑕 𝑥, 𝑡 = ∞

(𝐶𝑘

𝑐𝑜𝑠𝜔𝑘 𝑡 + 𝐷𝑘

𝑠𝑖𝑛𝜔𝑘

𝑡)𝑋𝑘 (𝑥) (1.26)

Trong đó k là các tần số riêng, Xk(x) là các hàm riêng.

Ta tìm nghiệm riêng bài toán tuyến tính không thuần nhất dưới dạng up(x,t) = Up(x) cost (1.27)

Thế biểu thức (1.27) vào phương trình (1.23) ta nhận được phương trình vi

phân thường

d 2U

p 

dx2

2



c2 U p  0

(1.28)

Nghiệm tổng quát của phương trình (1.28) có dạng

U xB cos x B sin x

p

Vậy ta có:

1 c 2 c

u x,t  (B cos x B sin x) cos t

(1.29)

p 1 c 2 c

Các hằng số B1 và B2 được xác định từ các điều kiện biên (1.24) up(0,t) = 0 :B1=0

EAup’(l,t) = F0cost :

EAB

 cos l F

B2 

F0

EA  cos l

c c

2 c c0

Nghiệm riêng (1.27) bây giờ có dạng

sin Ω x

up x,t 

F0c c EAΩ cos Ω l

c

cos Ωt

(1.30)

Nghiệm tổng quát (1.25) là tổng của hai nghiệm (1.26) và (1.30). Các hằng số Ck và Dk được xác định từ các điều kiện đầu.

Trong các hệ kỹ thuật, thường tồn tại thành phần cản. Do đó với t đủ lớn,

nghiệm của bài toán thuần nhất sẽ dẫn tới không. Ta chỉ cần quan tâm đến nghiệm riêng (1.30).

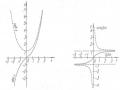
Trên hình (4.5b) biểu diễn đồ thị biên độ dao động dọc của điểm cuối thanh (x=1) theo tần số Ω. Trong đó ký hiệu

sin Ω l

U l F0lc cos Ωt; U * l F0l

p EA Ω l cos Ω l l c

p EA

p

Khi Ω → 0,do

sin l l,cos l  1 nên

U p (1)  1

với

U * 1

F0l là

c c c U * (1) p E A

độ dãn tĩnh của thanh. Do phương trình đặc trưng dao động dọc tự do là

cos Ω l  0 ,

c

xem phương trình (1.9), nên khi Ω → 𝜔𝑘 (tần số riêng) thì biền độ dao động cưỡng

bức tăng lên vô cùng (do

cos Ω l  0 ). Vậy hiện tượng cộng hưởng xảy ra khi

c

Ω = 𝜔𝑘 (𝑘 = 1,2, … ). Chú ý răng biểu thức nghiệm riêng (1.30) chỉ sử dụng được khi Ω ≠ k. Khi Ω → 𝜔𝑘 , biểu thức có nghiệm riêng có dạng

Up(x,t) = Up(x)tcosΩt (1.31)

Việc tìm nghiệm riêng trong trường hợp này đã được xét trong chương 2.

Bây giờ ta chuyển sang xét bài toán dao động dọc cưỡng bức của thanh thẳng đồng chất thiết diện không đổi, trên thanh chịu tác dụng của lực dọc trục cường độ p(x,t). Khi đó phương trình vi phân dao động dọc cưỡng bức không cản của thanh có dạng

2u 

2 2u p(x,t)

t2

c x2 

(1.32)

Áp dụng phương pháp khai triên theo các hàm riêng, ta tìm nghiệm riêng của phương trình (1.32) dưới dạng



u(x,t) qi(t) Xi(x)

i1

Trong đó Xi(x) là các hàm riêng, được xác định từ phương trình

(1.33)

X '' x

iX

x 0

(1.34)

2

i c i



Thế biểu thức nghiệm (1.33) vào phương trình (1.32) ta có

∞

u x,t = q

2 '' 1

i=1

i t Xi

x -c qi t Xi (x) = μ p(x,t)

Chú ý đến (1.34) phương trình trên có dạng

∞

q i t X

x + 21

𝑖=1

i ω qi t Xi x = μ p

x,t

Nhân hai vế của phương trình (1.35) với hàm riêng Xk(x) rồi lấy tích phân theo chiều dài của thanh

∞ 1 11

qitXix + ω2qi t 𝑋𝑖x 𝑋𝑘x(dx) = μ𝑝 𝑥, 𝑡 𝑋𝑘𝑥 𝑑𝑥

𝑖=1 0 0

Do tính chất trực giao của các hàm riêng, từ phương trình trên ta suy ra hệ phương trình vi phân thường.

q&&t2q

t0px,t Xkxdx f

t 

(k  1, 2,)

(1.36)

1

1 2

k k X xdxk



0k

Giải hệ phương trình dạng tọa độ chính (1.36) ta xác định được các hàm qk(t).

Sau đó thế vào biểu thức (1.33) ta tìm được nghiệm riêng của phương trình (1.32).

4.1.3 Dao động dọc tự do của thanh có tiết diện thay đổi

Phương trình dao động dọc tự do của thanh thẳng đồng chất tiết diện biến đổi chính là phương trình (1.2)

2u u 

xt2x EAxdx  0

(1.37)

Ta tìm nghiệm của phương trình (1.37) dưới dạng

u(x,t) = X(x)sin (t + ) (1.38)

Thế biểu thức (1.38) vào phương trình (1.37) ta nhận được phương trình vi phân thường đối với X(x)

2xX xE d AxdX  0

(1.39)

x dx 

Thực hiện phép đổi biến

x lX ' dX

d

l dX

dx

(1.40)

Giả sử 𝐴 𝜉 = 𝐴0𝑓 𝜉 → 𝜇 = 𝜌𝐴 = 𝜌𝐴0𝑓(𝜉) (1.41)

Chú ý đến các hệ thức (1.40) và (1.41), phương trình (1.39) được viết gọn lại dưới dạng

𝑓 𝜉 𝑋′′ + 𝜆2𝑓 𝜉 𝑋 = 0 (1.42)

Trong đó ta sử dụng ký hiệu

2 ,

2 2l2

c

c2 E



(1.43)

Cùng với các điều kiện biên, từ phương trình (1.42) ta có thể tìm được các hàm riêng 𝑋𝑖𝜉 và các giá trị riêng 𝜆𝑖𝑖 = 1,2, … . .

Bây giờ ta xây dựng một phiếm hàm mà phương trình vi phân (1.42) là phương

trình Euler của bài toán biến phân tương ứng. Phiếm hàm có dạng

1 1

Φ, X , X 'fX' 2 2fX2dFd

0 0

Điều kiện cần để phiếm hàm (1.44) đạt cực trị là

(1.44)

d F

F  0



dX ' X

Ở đây ta có

F 2 f X ' ,

X '

F2f X .

X

Phương trình vi phân Euler có dạng

𝑓 𝜉 𝑋′′ + 𝜆2𝑓 𝜉 𝑋 = 0

Như thế ta đã chuyển bài toán tìm nghiệm phương trình vi phân (1.24) về bài toán tìm cực trị của phiếm hàm (1.44)

Bây giờ ta áp dụng phương pháp Ritz để tính các tần số riêng dao động dọc của thanh có thiết diện biến đổi. Theo phương pháp Ritz, các hàm riêng 𝑋 𝜉 được chọn một các gần đúng dưới dạng

𝑘=1

𝑋 𝜉 = 𝑛

𝑎𝑘 𝑋𝑘 (𝜉)

(1.45)

Trong đó: ak là các hằng số, 𝑋𝑘 (𝜉) là các hàm tọa độ được chọn một các tùy ý, miễn sao thỏa mãn các điều kiện biên hình học. Các hằng số ak được chọn sao cho phiếm hàm

đạt cực trị

Φ, X , X ' f [ X ' 2 2 X 2 ]dFd

1 1

0 0

(1.46)

Thế biểu thức (1.45) và0 (1.46) ta được

1 n

n



' 2 2 2

Φa1,a2,, anf(akXk)(akXk)d

0 k 1 k 1 

Φ 𝑎

, 𝑎

, … , 𝑎 =

𝑓 𝜉 [𝑎2(𝑋′ − 𝜆2𝑋2) + ⋯ + 2𝑎 𝑎

𝑋′ 𝑋′ − 𝜆2𝑋 𝑋 +

1

1 2 𝑛0

1 1 1

1 𝑛

1 𝑛

1 𝑛

+𝑎2(𝑋′ 2 − 𝜆2𝑋2) + ⋯ + 2𝑎2𝑎𝑛𝑋′ 𝑋′ − 𝜆2𝑋 𝑋 +

2 2 2

2 𝑛

2 𝑛

…………….

+𝑎2 (𝑋′ 2 − 𝜆2𝑋2)]𝑑𝜉 (1.47)

𝑛 𝑛 𝑛

Thực chất của phương pháp Ritz là chuyển bài toán tìm cực trị của phiếm hàm (1.44) về bài toán tìm cực trị của hàm nhiều biến (1.47). Điều kiện cần để hàm Φ 𝑎1, 𝑎2, … , 𝑎𝑛đạt cực trị là