Các Phương Trình Đặc Trưng Và Các Trị Riêng Của Một Số Dầm

Bảng 4.2 Các phương trình đặc trưng và các trị riêng của một số dầm

4.3.3 Dao động uốn cưỡng bức của dầm Euler-Bernoulli đồng chất tiết diện không đổi

Đoạn này ta xét bài toán dao động uốn cưỡng bức dầm đồng chất tiết diện không đổi theo mô hình Euler-Bernoulli, chịu tác động của ngoại lực theo phương vuông góc với trục của dầm. Phương trình vi phân dao động uốn cưỡng bức của dầm Euler-Bernoulli có dạng (xem phương trình 3.18)

4w EI x4

2w

t2

p(x,t)

(3.41)

a. Biến đổi phương trình đạo hàm riêng (3.41) về hệ phương trình vi phân thường

Có thể bạn quan tâm!

• Các Điều Kiện Biên Của Một Vài Dạng Liên Kết
• Thiết Lập Phương Trình Vi Phân Dao Động Uốn Của Dầm
• Dao Động Uốn Tự Do Của Dầm Euler- Bernoulli Đồng Chất Tiết Diện Không Đổi
• Dao động kỹ thuật - 21
• Dao động kỹ thuật - 22

Xem toàn bộ 182 trang tài liệu này.

Áp dụng phương pháp Bernoulli, ta tìm được nghiệm phương trình (3.41) dưới dạng



w(x,t) Xi(x)qi(t)

i 1

Trong đó: Xi(x) là các đạo hàm riêng.

Thế biểu thức (3.42) vào phương trình (3.41) ta được:

(3.42)



EIX(IV) (x)q (t) X (x)q(t)p(x, t)

i t i i

i 1

Từ đó suy ra

EI

X IV (x) 

p(x,t)



qi(t) 

i 1 

i

Xi (x)

qi (t)Xi (x) 





Chú ý đến các biểu thức (3.23) ta có:

EI X IV (x) 2

i

i

Xi (x)

(3.43)

Thế (3.43) vào phương trình trên ta được



q(t) 2q (t)X (x) p(x, t)

i

i 1

i i i 

Nhân cả hai vế của phương trình này với hàm riêng Xk(x) rồi lấy tích phân dọc theo chiều dài của thanh



2

1

11

i 1

qi (t) 

i qi (t)

X (x) X (x)dx p(x,t)X (x)dx

0

0

i k k

Do điều kiện trực giao của các đạo hàm riêng ta suy ra

1

px,t X k (x)dx

q(t) 2q (t) 0h (t)

(3.44)

k k k

1 k

2

X k (x)dx

0

Như thế ta đưa việc giải phương trình đạo hàm riêng (3.41) về việc giải hệ phương trình vi phân thường (3.44). Dưới đây ta xét một số dạng cụ thể của hàm kích động p(x,t).

b. Lực kích động tập trung điều hoà

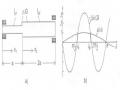
Xét dao động uốn của dầm chịu lực kích động tập trung điều hoà F0cost như hình 4.20a. Theo công thức (3.31) hàm riêng Xk(x) có dạng

X (x)  sin kx

k l

Trước hết ta tích phân

1 1 kx

2

1 1 kx 1

kx 11

Xk (x)dx

0

sin2

0

dx 

l l

 sin2 

 4 l  2

k 2 

0

ya

F=F0 cost

F=F0 cost

l/2Wmax

l

x

Al=const

l

z

a) b)

Hình 4.16 Dầm chịu lực kích động tập trung điều hoà

1

Để tính tích phân

px, t X k (x)dx

0

trong trường hợp này ta sử dụng khái niệm

hàm Delta-Dirac. Theo định nghĩa hàm Delta-Dirac được xác định bởi hệ thức:



(x a)  0 khi x  a và

(x a)dx  1



(3,45)

Hàm này có tính chất:



f (x)(x a)dx f (a)



(3.46)

Áp dụng vào bài toán của ta. Từ biểu thức: p(x,t) = F0cost.(x-a) Ta suy ra:

1 1

F0 cos t.(x a)X k (x)dx F0 cos t (x a)X k (x)dx

0

1

F0 cos t sin

0

kx l

0

(x a)dx F0 cos t sin

ka l

Phương trình (3.44) bây giờ có dạng

0

0

F cos t sin ka2F sin ka

l

q(t) 2q (t) llcos t

(3.47)

l

k k k



2

Nghiệm dừng của phương trình (3.47) theo chương 2 có dạng

k

q (t) 

2F0

sin ka

l

cos t

(3.48)

k l(2 2 )

Nghiệm tổng quát của phương trình (3.41) trong trường hợp này có dạng

2F sin ka

0

w(x,t) X (x)q (t) l sin kxcos t

k k

k

k 1

k 1

l(2 2 ) l

sin ka

w(x,t)  2F0 cos t lsin kx

(3.49)

k

l k 1 2 2 l

điểm t.

Công thức (3.49) là biểu thức tính độ vòng ở vị trí x bất kỳ của dầm tại thời

Khi a = l/2, ta có

sin k

w(x,t)  2F0 cos t 2sin kx

(3.50)

k

l k 1 2 2 l

Chú ý rằng:

2 

EI



k22

l 2

EI



k

k l 2

Nếu ta đưa vào ký hiệu:

k 2 

l 2

2

EI



k

Thì công thức nghiệm (3.49) có dạng

3 sin ka

w(x,t) 2F0l

cos t lsin kx

l 2

2

EI

4 EI k 1 k 2 2 l

Để minh hoạ ta lấy

a 1

2

và 

 0,7 . Khi đó ta có thể tính độ vòng ở

giữa dầm một cách tương đối đơn giản (hình 4.16b)

3

1 2F0l

cos t 

sin2 k

k 1

2

w( ,t) 

2

4 EI

k 2  0,49

Chú ý rằng: 1 1 1 1 1 ...  1,975

k 4  0,49 0,51 80,51 624,51 1295,51

Do đó:

w( 1

2

F l3cos t

,t) 0

24,65EI

F l3

Biên độ dao động giữa dầm là:

wmax 0

24,65EI

Nếu dầm chịu tác dụng của lực F(t) = F0 = const ở giữa dầm, theo Sức bền vật

F l3

liệu [6,7] độ vòng tĩnh ở giữa dầm là:

wt 0

48EI

Như thế độ vòng cực đại ở giữa dầm lớn gần gấp đôi vòng tĩnh tại đó. Ngoài ra chú ý rằng khi:

 = k2  = k

thì xảy ra hiện tượng cộng hưởng. Do có lực cản và do liên kết hình học nên biên độ dao động ở vùng cộng hưởng tăng lên khá lớn, tuy nhiên không tiến tới vô cùng như khi giả thiết bỏ qua lực cản.

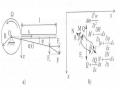
c. Lực di động có trị số không đổi

Xét bài toán dao động uốn của dầm hai đầu bản lề dưới tác dụng của lực F0 = const di chuyển với tốc độ v không đổi (Hình 4.17).

F0

v

x

El=const

l

z

Hình 4.17 Dầm chịu tải trọng di động

Ta đã biết các hàm riêng của dầm hai đầu chịu liên kết bản lề:

X (x)  sin kx

k l

1 1

2

Do đó:

X k (x)dx 

2

0

Sử dụng hàm Delta-Dirac, tải trọng p(x,t) trong bài toán này có dạng p(x,t) = F0(x-vt)

Do tính chất của hàm Delta-Dirac (công thức 3.46) ta có

1

F0 sin

0

kx l

(x vt)dx F0 sin(

kv t) l

Phương trình (3.44) đối với bài toán này có dạng

q(t) 2q (t) 2F0 sin t

(3.51)

k k k l k

Trong đó ta đưa vào ký hiệu:

kv

k l

(3.52)

nghiệm tổng quát của phương trình (3.51) đã được tính toán kỹ trong chương 2 có dạng:

q (t) A

cost B

sin t 

2F0

sin t

(3.53)

k k k k

k l(2 2 ) k

k k

Các hằng số Ak, Bk được xác định từ các điều kiện đầu. Giả sử cho biết điều kiện đầu



w0 (x) w(x,0) Xi(x)qi(0)  0

i 1

v(x) w(x,0)

X (x)q(0)  0

(3.54)

0 t

i i

i 1

Do tính chất trực giao của các hàm riêng, từ các điều kiện đầu (3.54) ta suy ra

qk(0) = 0,

qk(0)  0,

k = 1,2,… (3.55)

Với các điều kiện đầu (3.55), từ (3,53) ta dễ dàng xác định được các hằng số

Ak, Bk

A o,

B 

2F0k

(3.56)

k k l(2 2 )

k k k

Thế (3.56) vào biểu thức (3.53) ta được

qk (t) 

2F0

l(2 2 )

sin kt 

2F0

l(2 2 )

sin kt

(3.57)

k k k k

Theo công thức (3.42) biểu thức tính độ vòng của dầm có dạng



w(x,t) 

X (x)q (t) 2F0 

1 t k sin

kx



k k l

2 2 sin k 

k t sin l

k 1

Nếu ta đưa vào ký hiệu

k 1 k k 

k 

(3.58)

k

k



(3.59)

k

Thì:

2F0 1  2F0

1  2F0l31

l 2 2 l2 12 k 44EI 12

k k k k k

Biểu thức (3.58) bây giờ có thể viết lại dưới dạng như sau

3 

 2F l 1 



kx

w(x,t)

0

k

4 EI k 1 k

4 (1 2 )

sin k t

k sin

k t sin l

(3.60)

Hiện tượng cộng hưởng xảy ra khi k = k. Chú ý đến các biểu thức (3.30) và (3.52) ta dễ dàng xác định được vận tốc tới hạn vkth.

k = k 

vkth

k

EI



l

Ở vùng cộng hưởng, độ vòng của dầm sẽ đạt giá trị lớn nhất. Ta xác định độ vòng của dầm khi v = vth. Không giảm tính tổng quát ta giả sử 1 = 1. Khi đó trong tổng (3.60) ta chỉ cần giữ lại số hạng ứng với k = 1. Để đơn giản cách viết ta bỏ chỉ số 1 ở 1 và 1 đi. Vậy ta có:

2F l3 x

sin t  sint

w (x,t) 0 sin lim

th 4 EI

l 

12

2

Ở đây biểu thức cần tính giới hạn có dạng

(L’Hospital) ta tính được:

0 . Áp dụng quy tắc Lôpital

0

3

w (x,t) 2F0l

t cos t 1 sin t 3

x 2F0l

sin lim

sin x(sint t cost)

th 4 EI

l 

2

 2 2

4 EI l

Thay v

(biểu thức 3.52) vào biểu thức trên ta được

l th

F0l3 vth vth vth x

wth (x,t) 4 EI sin l t l t cosl t sin l

(3.62)



Tìm cực trị của hàm (3.62) theo t. Muốn vậy ta tính đạo hàm riêng theo t và cho bằng không

wth (x,t)  0

t l

t vth

Từ đó ta có:

wth max

(x) 1

3

F0l3 sin x EI l

(3.63)

Khi x = l/2, độ vòng cực đại ở điểm giữa dầm là

w 1 1 F0l3

th max ( 2)3 EI

(3.64)

Từ giáo trình Sức bền vật liệu, người ta tính được độ vòng tĩnh ở điểm giữa dầm khi có lực F0 = const tác dụng ở giữa dầm là:

wt 

F0l3

48EI

Như thế, độ vòng cực đại (364 lớn gấp rưỡi độ vòng tĩnh.

l

Khi v << vlth, tức là 

đúng xác định độ vòng

l 1 , từ biểu thức (3.60) ta suy ra công thức gần



l

w(x,t) 2F0l3

1sin kxsin kvt 

4 EI k 4

l l 

(3.65)

k 1 

Đó là biểu thức xác định độ vòng tĩnh của dầm chịu tác dụng của lực F0 đặt ở điểm cách xa đầu bên trái dầm một đoạn vt mà chúng ta đã biết trong giáo trình Sức bền vật liệu.

4.3.4 Dao động uốn tự do của dầm Timoshenko

1. Dao động uốn tự do dầm Timoshenko tiết diện không đổi

Từ phương trình (3.16), cho p(x,t) = 0, ta nhận được phương trình dao động tự do của dầm Timoshenko

4w

2w

E 4w

2 I

4w

EI x4

A t2

I 1

k *G x2t2 k *G

t4  0

(3.66)



Ta tìm nghiệm của phương trình (3.66) dưới dạng

w(x,t) X (x) cos(t )

(3.67)

Thế biểu thức (3.67) vào phương trình (3.66) và thực hiện một vài phép biến đổi sơ cấp ta nhận được phương trình vi phân thường

i

d 4 X 4 2

dx4

(1)

d 2 X

dx2

4

(1

4i4) X  0

(3.68)

Trong đó ta đưa vào các ký hiệu

4 2 A,

EI

i 2 I ,

A

E k *G

Xét trường hợp hai dầm có liên kết bản lề (hình 4.17a). Khi đó ta tìm nghiệm phương trình (3.68) thoả mãn các điều kiện biên dưới dạng

X k (x) Bk

sin kx ,

l

k = 1,2,… (3.70)

Thế biểu thức (3.70) vào phương trình (3.68) ta nhận được phương trình đặc trưng để xác định y

k4 k2



l 

i2 (1)

l

(1i4)  0



(3.71)

Phương trình (3.71) là phương trình bậc hai đối với hàm 4. Giải ra ta được



4

k1,k 2

2 



k1,k 2 

1 ki 2

ki 2

ki 4 

11

1 2(1)

 (1)2 

2i4

l l

l 



(3.72)

Khác với lý thuyết dầm Euler-Bernoulli, ở đây ứng với mỗi giá trị của k ta có hai trị riêng khác nhau k1>k2. Như thế ứng với mỗi hàm riêng Xk(x) ta có hai tần số riêng k1 >k2. Sở dĩ có hiện tượng đó là vì trong lý thuyết dầm Euler-Bernoulli độ vòng w và góc xoay  có liên quan với nhau w’ = , còn trong lý thuyết dầm Timoshenko chúng là hai đại lượng độc lập với nhau.

Về mặt kỹ thuật người ta ít quan tâm đến các tần số cao (ứng với dấu cộng trước căn trong (3.72)). Ta xét trường hợp ứng với dấu trừ trước căn. Trong trường hợp ki/l<<1, áp dụng khai triển

1x

 1xx2 x3  ...

2 8 16

với |x|  1

Ta có công thức gần đúng với căn thức trong (3.72)

ki 2

2 ki 4

ki 2

1 21l 1l  11l 



ki 4 ki 2 

 2l 1 21l  ...



Từ đó ta nhận được biểu thức gần đúng xác định các tần số riêng

EI

l4

ki 2 

k k 211

(3.73)

l

Chú ý rằng, tần số riêng của dầm Euler-Bernoulli được xác định bởi công thức

(3.30)

EI

l4

k k 2

Như thế số hạng thứ hai trong dấu ngoặc vuông của công thức (3.73) thể hiện sự khác nhau giữa các tần số riêng tính theo lý thuyết Timoshenko và lý thuyết Euler- Bernoulli. Độ lớn của số hạng này phụ thuộc vào độ mảnh  = l/i của dầm, vào chỉ số k và vào hệ số 1 + . Đối với dầm có thiết diện hình chữ nhật, chiều cao h, nếu k* = 5/6, E/G = 8/3 thì số hạng (1 + )(ki/l)2 sẽ bằng 3,45(kh/l)2. Nếu l/h = 10 thì độ chênh lệch tần số riêng cơ bản (k=1) giữa lý thuyết Timoshenko và lý thuyết Euler-