A Mô Hình Dao Động Bộ Tắt Chấn Động Lực Có Tính Đến Ma Sát Nhớt

Trong đó

i , i , i

được xác định bởi công thức (2.28) và (3.12) còn hi tính

theo công thức (3.27). Việc tìm nghiệm của phương trình (5.33) đã được trình bày trong chương 2.

Thí dụ 3.13: Xét mô hình dao động trong thí dụ 3.12. Giả sử trên vật thứ 2 tác

dụng một lực

F2 (t) Fˆ

sin t

theo chiều q2. Hãy viết phương trình vi phân dao động

2

Có thể bạn quan tâm!

• Đỗ Vòng Và Góc Xoay Của Đường Đàn Hồi Của Các Dầm Thẳng Có Tiết Diện Không Đổi.
• Phương Pháp Giải Trực Tiếp (Ma Trận Cản Tùy Ý)
• Phương Pháp Ma Trận Dạng Riêng (Ma Trận Cản Đặc Biệt)
• Dao Động Dọc Tự Do Của Thanh Đồng Chất Tiết Diện Không Đổi
• Các Điều Kiện Biên Của Một Vài Dạng Liên Kết
• Thiết Lập Phương Trình Vi Phân Dao Động Uốn Của Dầm

Xem toàn bộ 182 trang tài liệu này.

dạng toạ độ chính. Tìm dao động cưỡng bức bình ổn.

Lời giải: Phương trình vi phân dao động cưỡng bức có dạng:

1 0q&&1b bq&12c

cq1 0 

0 1q&&b b q&

c 2cqFˆ sin t 

2 2 



2 2 

Chia hai vế của phương trình trên cho m và sử dụng các ký hiệu như ở thí dụ

3.12 ta được:

1 0q&&1 2D  1

1q&12 2

1q1 0 

0 1q&&

01 1 q&

0 1 2 q 

Fˆ

sin t / m

2 

2 



2 2 

Trong thí dụ 3.12 ta đã tính được ma trận dạng riêng

V  1 1



1 1 

1 10

Fˆ sin t 

Do đó: VT f

ˆ

2

1 1 F2 sin t / mm sin t 

Hệ phương trình vi phân dao động cưỡng bức dạng toạ độ chính

2 Fˆ

&p&1 40Dp&1 30p1 2 sin t

2m

(3.34)

2 Fˆ

&p&20p2 2 sin t

2m

(3.35)

Ở trạng thái chuyển động bình ổn (bỏ qua thành phần dao động tự do) nghiệm của các phương trình (3.34) và (3.35) có dạng:

p1(t) M1 sin t N1 cos t

Fˆ 1

2m 2 2

p2 (t) 2sin t M 2 sin t

0

(0 )

Trong đó:

0 2

0 0

M1 

(322)Fˆ

N 

2m (322)2162D22

2

40 DFˆ

0 0

12m (322)2162D22

Từ hệ thức q = Vp ta suy ra các biểu thức đối với các tọa độ q1, q2 ban đầu

q1(t) = (M1 + M2)sint + N1cost

q2(t) = (M2 – M1)sint - N1cost (3.36)

MỘT SỐ BÀI TOÁN ÁP DỤNG

* Bộ tắt chấn động lực không tính đến ma sát

a) Lý thuyết: Xét phương trình vi phân dao động cưỡng bức của hệ hai bậc tự do không cản

q 1 c c q f1

m11 m12 11 12 1

+ = (3.37)

m21 m22 q 2 c21 c22 q2 f2

Giả sử các lực kích động có dạng

f1t =f1

sin Ωt + α , f2

t =f2

sin Ωt + α (3.38)

Ta tìm nghiệm của hệ phương trình (3.37) dưới dạng

q = A1sin Ωt + α (3.39)

A2

trong đó A1 , A2 là các hằng số cần xác định.

Thế các biểu thức (3.29) vào phương trình (3.37) ta nhận được hệ phương trình đại số tuyến tính để xác định A1 và A2

c11 − m11 Ω2A1 + c12 − m12 Ω2A2 =f1

c21 − m21 Ω2A1 + c22 − m22 Ω2A2 =f2

Giải hệ phương trình đại số tuyến tính (6.4) ta được

(3.40)

c  m Ω2 fˆ c  m Ω2 fˆ

A1 

22 22 1 12 12 2

Δ

(3.41)

c  m Ω2 fˆ c  m Ω2 fˆ

A2 

Trong đó

11 11 2 21 21 1

Δ

 m Ω f

c 2 ˆ

Δ = c11 − m11 Ω2c22 − m22 Ω2− c12 − m12 Ω2c21 − m21 Ω2(3.42) Xét trường hợpf2 = 0. Khi đó từ công thức (3.41) ta suy ra

A1 

22 22 1

 m Ω f

Δ

(3.43)

A2 

c

2 ˆ

21 21 1

Δ

Khi Δ ≠ 0, nếu ta chọn các tham số của hệ sao cho c22 − m22 Ω2 = 0 thì

fˆ

A1  0, A2 1

(3.44)

c  m Ω2

12 12

Vậy khi Ω2 = c22m22

nhất được hoàn toàn dập tắt.

thì dao động cưỡng bức ứng với toạ độ suy rộng thứ

b) Nguyên lý thiết kế bộ tắt chấn động lực: Dựa trên lý thuyết ở trên, người ta chế tạo các thiết bị tắt dao động gọi là bộ tắt chấn động lực (Absorber). Giả sử ta có mô hình dao động xoắn như hình 3.17a. Dễ dàng tính được biểu thức động năng và thế năng

1 1

T = J φ 2 , Π = c φ2

2 1 1 2 1 1

và lực suy rộng Q = M1t =f1

sin Ωt + α . Phương trình vi phân dao động

của hệ trên hình 3.17a có dạng

J1φ 1 + c1φ1 = f1

sin Ωt + α (3.45)

Ở chế độ chuyển động bình ổn, dao động cưỡng bức của hệ có dạng

fφ  sin Ωt  α

ˆ

1

1

(3.46)

J ω2 Ω2

1 1

1

trong đó ω2 = c1J1

c1

M1(t)

a)

J1

1

c1

c2

M1(t)

b)

J1

J2

1 2

Hình 3.12 Mô hình dao động xoắn

Gắn vào mô hình 3.12a một hệ phụ như hình 3.12b. Mô hình 3.12b là một hệ cơ học gồm hai bậc tự do. Hệ phương trình vi phân dao động của hệ này có dạng

J1φ&&1 c1φ1 c2φ1 φ2 fˆsin Ωt  α

1

J2φ&&2 c2φ1 φ2 0

(3.47)

Điều kiện dập tắt dao động φ1 là Ω2 = c2J2. Khi đó ta có

φ1  0

2 c

1

φ fˆ sin sin Ωt  α

2

(3.48)

Hệ phụ lắp thêm vào hệ 3.12a như trên hình 3.12b được gọi là bộ tắt chấn động lực. Khi thiết kế bộ tắt chấn động lực trong thí dụ trên ta phải chú ý đến hai điều sau:

- Chọn hệ số cứng c2 sao cho biên độ dao động cưỡng bức của góc φ2(t) là

f1

c2

có thể chấp nhận được.

- Chọn mômen quán tính khối J2 sao cho Ω2 = c2J2.

** Bộ tắt chấn động lực có tính đến ma sát nhớt

Ở đoạn trên, ta đã trình bày lý thuyết bộ tắt chấn động lực không tính đến ma

sát. Dao động của vật thể thứ nhất hoàn toàn được dập tắt khi ta lắp vào hệ bộ tắt chấn

động lực. Khi lắp vào hệ bộ tắt chấn động lực thì hệ sẽ có hai tần số riêng. Nếu tần số của lực kích động  trùng với một trong các tần số riêng thì không thể sử dụng bộ tắt chấn động lực không có ma sát nhớt được. Dưới đây ta trình bày lý thuyết bộ tắt chấn động lực có ma sát nhớt.

Xét mô hình dao động như hình 3.13a.

Các biểu thức động năng, thế năng và hàm hao tán của hệ có dạng:

T 1m x21m x2

2 1 1 2 2 2

1 c x2 1 c (x x )2

2 1 1 2 2 2 1

1b(xx)2

2 2 1

c1

F0 cost

b

2

c

m1 m2X

X 1 X 2

Hình 3.13a Mô hình dao động bộ tắt chấn động lực có tính đến ma sát nhớt

Giả sử trên vật thể m1 ta tác dụng một lực tuần hoàn F(t) = F0cost.

Thế các biểu thức động năng, thế năng, hàm hao tán và lực suy rộng vào phương trình Lagrange loại II ta nhận được phương trình vi phân dao động của hệ

m1

0x1b

bx1c1c2

c2 x1 F (t)

(3.48)

 0 m x

b

bx

c

c x 

0 

2 2 

2 2

2 2 

1

2

1

2

Để tìm nghiệm phương trình vi phân (3.48) ta áp dụng phương pháp biên độ phức.Ta đặt:

F(t) = F0eit,

x u~eit ,

x u~eit

(3.49)

Trong đó:

u~ , ~

là các hệ số phức cần xác định. Thế các biểu thức (3.49) vào

1

u

2

hệ phương trình vi phân (3.48) và ước lượng số hạng eit ta nhận được hệ hai phương trình đại số tuyến tính đối với hai ẩn là hai biên độ phức u~ , u~ .

1 2

(c c m 2ib)u~ (c ib)u~F

1 2 1 1 2 2 0

 (c ib)u~ (c m 2ib)u~ 0

(3.50)

2 1 2 2 2

Giải hệ hai phương trình đại số (3.50) ta được

u~F0(c m 2ib)

1 2 2

u~F0(c

ib)

(3.51)

2 2

2

Với  = (c1 – m12 )(c2 – m22 ) – m2c22 + ib(c1 – m12 – m22 )

F (c m 2 )2 b22



(c m  )(c m  ) m c b  (c m m  )

0 2 2

2

2

2

2

2 2

2

2

1 1

2

2

2 2

1 1

2

1

Ký hiệu: u1 và u2 tương ứng là trị tuyệt đối của các biên độ phức phương trình (3.51) ta tìm được:

u~ ,

u~ . Từ các

u1 

(3.52)

c1 m1

Nếu đưa vào các ký hiệu:

c

0

u F0 ;

1

(0) ;

c2 m2

2

(0) 

1

;

(0)

m2;

m

(0) ;

2

(0)

D b

2m (0)

(3.53)

1 1 1 2 1

(2 2 )2  4D22

(1-2)(22) 222 4D22(122)2

Thì từ (3.52) ta suy ra biểu thức độ lệch tương đối của khối lượng m1 (hay hàm khuyếch đại)

V u1

1 u

(3.54)

0

Tính toán tương tự ta được hàm khuyếch đại V2

2  4D22

(1-2)(22) 222 4D22(122)2

V u2

2 u

(3.55)

0

Hiệu quả làm việc của bộ tắt chấn động lực có ma sát nhớt phụ thuộc vào việc chọn các tham số , , D. Trước hết ta xét sự phụ thuộc của V1 vào tham số D

Khi D = 0 từ (3.54) ta có:

2 2

(1-2 )(2 2 ) 22

V1 

1

1- 1 2

Khi D  từ (3.54) ta suy ra

(3.56)

V1 

(3.57)

Trên hình 3.13b là đồ thị của sự phụ thuộc độ lệch tương đối V1 vào  (đồ thị biên độ- tần số) với D = 0; D = 0,1; D = 0,32 còn  = 1/20;  = 1 [12].

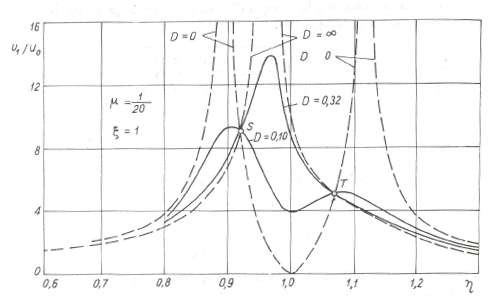
Hình 3.13b Đồ thị của sự phụ thuộc độ lệch tương đối V1 vào 

1

Các đường cong trên hình 3.18b đều đi qua hai điểm S và T. Điều đó có nghĩa là tồn tại hai trị số của  mà tại đó biên độ dao động của khối lượng m1 không phụ thuộc vào các hệ số cản b. Từ các biểu thức (3.56) và (3.57) ta suy ra phương trình xác định các trị số đó của 

2 2

(1-2 )(2 2 ) 22

 1- 12

(2 2 )(1-2 - 2 )  (1-2 )(2 2 ) 22

Rút gọn phương trình trên ta được:

2 2

4  22 1

2 

22



2 0

(3.58)



Phương trình (3.58) là phương trình đại số bậc hai đối với 2. Nghiệm của phương trình này là:



2

1,2

 1 1 (1)2 

2 

124 221

(3.59)

Trong đó 1 là hoành độ điểm s, 2 là hoành độ điểm T. Thế các biểu thức của

1 và 2 vào (3.57) ta nhận được cácc biểu thức xác định tung độ của các điểm S và T. Do 2 >1 nên từ (3.57) ta suy ra:

u1S

1

2

(3.60)

u0 1 11

u1T

1

2

(3.61)

u0 1 12

Theo (3.59) 1 và 2 là hàm của các tham số  và  nên các tung độ của các điểm S và T phụ thuộc vào  và . Theo các công thức (3.53) thì  và  phụ thuộc vào các khối lượng m1 và m2 và các hệ số cứng c1 và c2.

Nếu ta chọn trước m2 thì các chế độ làm việc của bộ tắt chấn động lực có cản nhớt sẽ đạt tối ưu khi tung độ các điểm S và T là như nhau và hệ số cảm sẽ được chọn sao cho ở các điểm này đường cong biên độ tần số đạt cực đại. Từ điều kiện tung độ các điểm S và T bằng nhau ta suy ra:

1

2 

1

2

1 11 1 12

Giải ra ta được:

2 2 2

1 2 1

Do 2 , 2 là hai nghiệm của phương trình bậc hai (3.58) nên theo định lý Vieta

ta có:

1 2

2 2 

12 2  2

1 2 2

2 1

Từ đó giải ra: 

1(3.62)

1

Thế biểu thức (3.62) vào phương trình (3.59) ta được



2 

2 1 





1,2 11

(3.63)

2

Thế 2 này vào biểu thức (3.63) ta được

u1T

u0

u1S

2 



u0

(3.64)

Vị trí của các điểm S và T không phụ thuộc vào các hệ số cản nhưng các giá trị cực đại tung độ của đường cong biên độ tần số thì phụ thuộc vào hệ số cản (xem hình 3.13b). Để cho đường cong biên độ tần số đạt cực đại tại các điểm S và T thì đạo hàm dV1/d = 0 khi  = 1 và  = 2. Thế các biểu thức của  theo (3.62) và của  theo (3.63) vào phương trình dV1/d = 0 và thực hiện một vài phép biến đổi ta nhận được hệ thức giữa tham số D và .

Tại S

D2 

(3 

)

2 

8(1 )3

Tại T

D2 

(3 

)

2 

8(1)3

Từ đó, để làm giá trị trung bình khi thiết kế, người ta đề nghị lấy:

D

2

optimal

 3

8(1)3

(3.65)

*** Dao động của mô hình ôtô hai bậc tự do

Một ôtô đang chạy với vận tốc v không đổi trên mặt đường không bằng phẳng (Hình 3.14a). Trong trường hợp nghiên cứu sơ bộ ta có thể xây dựng mô hình cơ học của ôtô bằng hệ hai bậc tự do như hình 3.14b.

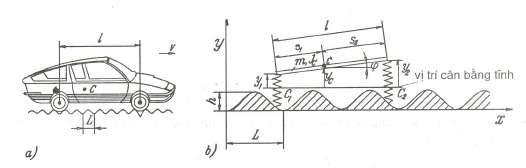
Hình 3.14 Mô hình dao động ôtô hai bậc tự do

Ta ký hiệu m là khối lượng ôtô, Jc là mômen quán tình khối của ôtô đối với trục đi qua khối tâm ôtô và vuông góc mặt phẳng hình vẽ, c1 và c2 là độ cứng lò xo, s1 và s2 là khoảng cách giữa hai bánh xe (l = s1 + s2).

Giả sử quy luật nhấp nhô của mặt đường được xác định bởi hàm tuần hoàn (xem hình 3.14b)

y* 

h (1 cos 2

2x*

)

L

Ta chọn các toạ độ suy rộng q1 = yc, q2 = . Biểu thức động năng và thế năng của hệ có dạng

T 1my21J

2

(3.66)

2 C 2C

1 c y2 1 c y2

(3.67)

2 1 1 2 2 2

Trong đó y1, y2 là biến dạng của các lò xo

2x

*

y1 = yC –y1* - s1; y2 = yC –y2* - s2; (3.68) Toạ độ các điểm tiếp xúc giữa lò xo và mặt đường là

x* vt ;

y* 

h (1 cos1 ) h (1 cos t)

1

2

x* vt l ;

1

1

y* 

2 L 2

2x

1 cos(t  22

*

h (1 cos2 ) h 

2 L 

1 )

L 

Trong đó ta đưa vào ký hiệu

2v

L

Thế các biểu thức (3.68) vào (3.67) ta được

(3.69)