Dao Động Uốn Tự Do Của Dầm Euler- Bernoulli Đồng Chất Tiết Diện Không Đổi

ảnh hưởng lớn đến các tần số dao động bậc cao. Cho I 0, ta nhận được phương trình vi phân dao động uốn của dầm Euler-Bernoulli



4w EI x4 

2w

t2

p(x,t)

(3.18)

Chú ý rằng trong trường hợp dầm Euler-Bernoulli ta có quan hệ Q M

x

4.3.2 Dao động uốn tự do của dầm Euler- Bernoulli đồng chất tiết diện không đổi

Trước hết ta xét dao động uốn tự do của dầm đồng chất tiết diện không đổi theo mô hình Euler- Bernoulli. Từ phương trình vi phân (3.18) ta có phương trình dao động uốn tự do

4w 

x4 EI

2w



t20

(3.19)

dạng

Áp dụng phương pháp Bernoulli, ta tìm nghiệm của phương trình (3.19) dưới

w(x,t) = X(x)T(x) (3.20)

Thế biểu thức (3.20) vào phương trình (3.19) ta được

T (t) X ( IV ) (x) 

EI

Từ đó suy ra:

T(x) X (x)  0

T(t) EI

X ( IV ) (x)

(3.21)

T (t)

X (x)

Do vế phải của phương trình (3.21) là hàm chỉ phụ thuộc vào x, còn vế trái là hàm chỉ phụ thuộc vào t, cho nên cả hai vế bằng một hằng sô. Do có chủ định trước, ta gọi hằng số đó là 2. Từ đó suy ra

T&&(t) 2

T (t)

EI X IV (x) 2

T&&t2Tt 0

IV 

2

(3.22)

X (x) 

X x

EI

X x 0

(3.23)

Nghiệm của phương trình (3.22) có dạng

T(t) = Acost + Bsint (3.24)

Trong phạm vi bài toán xác định các tần số dao động riêng, ta phải tìm nghiệm phương trình (3.23). Để biểu diễn nghiệm một các gọn gàng, ta đưa vào đại lượng không thứ nguyên 

I

4 2 4

EI

(3.25)

Khi đó, phương trình (3.23) có dạng

4

𝑋𝐼𝑉𝑥 − 𝜆𝑋 𝑥 = 0 (3.26)

𝑙

Ta tìm nghiệm của phương trình (3.26) dưới dạng

𝑋 𝑥 = 𝐶 cos 𝜆 𝑥𝑥

𝑥 + 𝐶 𝑠𝑖𝑛𝑕 𝜆 𝑥(3.27)

1 𝑙

+ 𝐶2sin(𝜆 𝑙) + 𝐶3𝑐𝑜𝑠𝑕 𝜆 𝑙 4 𝑙

Trong đó các hàm lượng giác cosx, sinx chúng ta quen biết từ học phổ thông, các hàm hyperbol coshx, sinhx chúng ta cũng đã quen biết trong giáo trình toán cao cấp. Ở đây nhắc lại một ít về định nghĩa và các tính chất sơ cấp của các hàm hyperbol.

Theo định nghĩa

sinhx 

ex ex

,

coshx 

ex ex

2 2

ex ex ex ex

suy ra

tghx  , cotghx 

ex ex ex ex

Đồ thị các hàm hyperbol có dạng như hình 4.12. Từ định nghĩa trên ta dễ dàng

sinh0 = 0 ; cosh0 = 1 ; tgh0 = 0 ; cotgh = 

Các hàm coshx, sinhx tuần hoàn chu kỳ 2i (i là đơn vị ảo)

sinh (x + 2k i) = sinh(x) cosh (x + 2ki) = cosh(x) còn các hàm tghx và cotghx hoàn chu kỳ i

tgh(x + 2ki) = tgh(x) cotgh(x + ki) = cotgh(x)

Đạo hàm các hàm sinhx, coshx có tính chất đặc biệt như sau (sinhx)’ = coshx, (coshx)’ = sinhx

Các hằng số C1, C2, C3, C4 trong biểu thức (3.27) được xác định từ các điều

kiện biên.

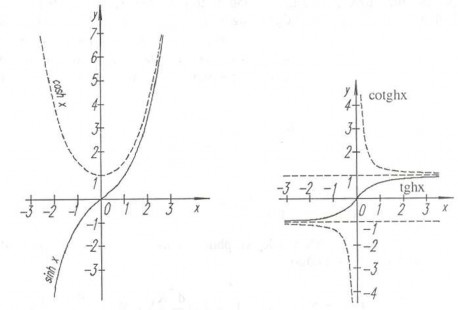
Hình 4.12 Đồ thị các hàm hyperbol

Ở đầu dầm có gối tựa bản lề, độ vòng và mômen uốn đều bằng không, do đó ta

có

d 2 X

X  0,

dx2  0

(3.28a)

Ở đầu dầm bị ngàm chặt, độ vòng và góc xoay đều bằng không, ta có

X  0,

dX  0

dx

(3.28b)

Ở đầu dầm tự do, mômen uốn và lực cắt đều bằng không, do đó

d 2 X dx2

 0,

d 3 X



dx30

(3.28c)

Ở hai đầu dầm, bao giờ cũng có bốn điều kiện biên. Từ các điều kiện biên, ta có thể xác định được các hằng số trong hệ thức (3.27). Trong quá trình đó, chúng ta sẽ nhận được phương trình đặc trưng. Giải phương trình đặc trưng ta nhận được các tần số riêng j. Ứng với mỗi tần số riêng j ta có mộ trị riêng j, và theo (3.27) ta có một hàm riêng Xj(x). Ta sẽ xét tính chất trực giao của các hàm riêng này. Giả sử Xj(x), Xk(x) là hai hàm riêng tương ứng với j, k. Từ phương trình (3.26) ta suy ra.

d 4 X (x) 4

jj

X (x)

dx4

l j

k

d 4 Xx

kX

x

dx4

l k

4



Nhân phương trình thứ nhất với Xk(x), phương trình thứ hai với Xj(x), trừ đi nhau rồi lấy tích phân theo x ta được

4 j 4k 1 1 

d 4 X

d 4 X 

4X jxX kxdx X jx

k X k xdx  0

j

4

4

l 0 0 

dx dx 

l





Bằng cách tích phân từng phần ta có

4 j 4k 1

d 3 X

d 3 X

dX d 2 X dX

d 2 X 

2

3

j

3

j j

2

4 X j xX k xdx X j

k – X k k

k 

l 0 

dx dx dx dx

dx dx 0

Nghiệm tổng quát của phương trình (3.19) có dạng



wx,t X k xAk cosktBk sinkt

0

Các hằng số Ak, Bk được xác định từ các điều kiện đầu

(3.29)

Để làm thí dụ ta xét dao động uốn tự do của dầm hai đầu tựa bản lề như hình 4.13a Các điều kiện biên trong bài toán này là độ vòng w(x,t) và mômen uốn M(x,t) triệt tiêu ở hai biên x = 0 và x = l

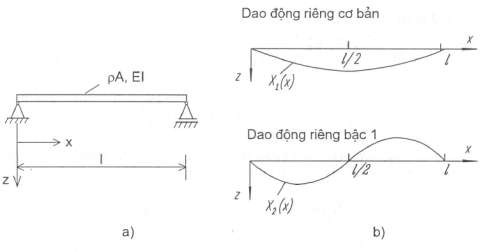
Hình 4.13 Dao động uốn tự do của dầm hai đầu tựa bản lề

w(0,t) = 0 M(0,t) = -EIw’’(0,t) =0

w(l,t) = 0 M(l,t) = -EIw’’(l,t) =0

Với các điều kiện biên này, từ biểu thức nghiệm (3.27) ta suy ra 4 phương trình để xác định các hằng số C1, C2, C3, C4

X(0) =0 : C1 + C3 = 0

X(l) = 0: C1cos  + C2sin  + C3cosh  + C4sinh  =0 X’’(0) = 0: - C1 + C3 = 0

X’’(l) = 0: - C1cos  + C2sin  + C3cosh  + C4sinh  =0

Từ các phương trình trên và do sinh  ≠0 nên C1=C3=C4=0. Mặt khác để cho C2≠0, ta có phương trình đặc trưng: sin  = 0

Giải ra ta được

EI



k2

k kk l  , k  1, 2,..,

(3.30)



Các hàm riêng (3.27) bây giờ có dạng

X xCksin 

xCk sin kx

(3.31)

k 2

Khi k=1,2 ta có

EI



2

k l 2 l

x

1 l 

, X xC1sin

1 2

l



EI





 22

, X xC2ssin

2x

2 l 

2 2 l



Các dạng dao động riêng cơ bản và dao động riêng bậc 1 vẽ trên hình 4.17b.

Biểu thức nghiệm tổng quát (3.29) trong thí dụ này có dạng

w x,t 

kx



sin A

cost B

sint 

(3.32)



k 1

l k k k k

2

Trong đó ta lấy 𝐶𝑘= 𝑙. Từ các điều kiện đầu

wx,0w

x,

w(x,0)v

(x)

0 t 0

Ta có các biểu thức để xác định Ak và Bk

kx

A sin w (x)

l

k 0

k 1

kx

B ω sin v (x)

l

k k 0

k 1

Chú ý đến tính chất trực giao của các hàm riêng (3.27), từ các biểu thức trên ta

suy ra

l 

2 1

Ak  w0 (x)sin

0

kx dx l

2 1 kx

Bkl v0(x)sin l dx

k 0

Bây giờ ta chuyển sang xác định các tần số riêng và các hàm riêng của dâm một đầu ngàm chặt, một đầu tự do hình 4.18a. Các điều kiện biên có dạng

w(0,t) = 0 M(0,t) = -EIw’’(0,t) =0

w(l,t) = 0 Q(l,t) = -EIw’’(l,t) =0

Với các điều kiện trên từ biểu thức nghiệm (3.27) ta suy ra hệ bốn phương trình tuyến tính thuần nhất

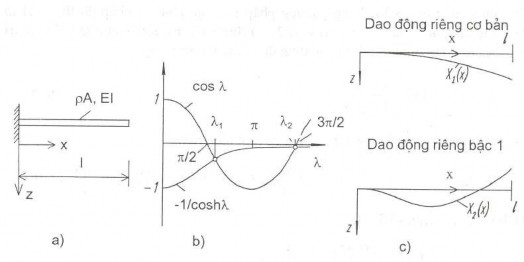
Hình 4.14 Dao động của dầm công xon

X(0)=0 :

C1	+	C3		= 0
X’(0)=0:		C2	+	C4	=0

Có thể bạn quan tâm!

• Dao Động Dọc Tự Do Của Thanh Đồng Chất Tiết Diện Không Đổi
• Các Điều Kiện Biên Của Một Vài Dạng Liên Kết
• Thiết Lập Phương Trình Vi Phân Dao Động Uốn Của Dầm
• Các Phương Trình Đặc Trưng Và Các Trị Riêng Của Một Số Dầm
• Dao động kỹ thuật - 21
• Dao động kỹ thuật - 22

Xem toàn bộ 182 trang tài liệu này.

X(l)=0: - C1cos  - C2sin  + C3cosh  + C4sinh  =0 X’’(l)=0: C1sin  - C2cos  + C3 sinh  + C4 cosh  =0

Từ hai phương trình đầu của hệ bốn phương trình trên ta suy ra C1=-C3, C2=-C4 Sau đó thế vào hai phương trình sau ta được

C1(cos  +sinh  ) + C2(sin  + sinh  ) = 0

C1(sin  + sinh  ) – C2(cos  +cosh  ) = 0 (3.33)

Điều kiện cần để cho C1, C2 không đồng nhất triệt tiêu là định thức các hệ số phải bằng không

 cos  cosh sin  sinh 

sin  sinh 

(cos  cosh )  0

Từ đó ta nhận được phương trình đặc trưng

Cos  cosh  +1 = 0 (3.34)

Giải phương trình (3.34) bằng phương pháp số hoặc phương pháp đồ thị ta nhận được tập vô hạn nghiệm  =i (i = 1,2,.., ) (hình 4.14b). Khi biết được các giá trị riêng

i từ công thức (3.24) ta xác định các tần số riêng

EI



2

i i

l2

Ứng với mỗi trị riêng i , theo (3.27) ta có một hàm riêng

𝑋 𝑥 = 𝐶𝑖cos𝜆𝑖 𝑥+ 𝐶𝑖sin𝜆𝑖 𝑥+ 𝐶𝑖cosh𝜆𝑖 𝑥+ 𝐶𝑖sinh𝜆𝑖 𝑥

(3.35)

(3.36)

𝑖 𝑙

𝑙 2

𝑙 3

𝑙 4 𝑙

Từ hệ phương trình (3.33) ta suy ra

Ci cos i  cosh i C(i)

2 sin  sinh 1

Do đó

i i

𝐶𝑖 = −𝐶𝑖 = cos 𝜆𝑖 + cosh 𝜆𝑖𝐶(𝑖)

4 2 sin 𝜆𝑖 +sinh 𝜆𝑖 1

Mặt khác như trên đã chỉ ra 𝐶𝑖= −𝐶𝑖

3 2

Thế 𝐶𝑖, 𝐶𝑖, 𝐶𝑖xác định theo 𝐶𝑖vào biểu thức (3.36) ta được dạng cụ thể

2 3 4 1

của hàm riêng Xi(x)

XxCicos i x  cosh i x cos i  cosh i sin i x  sinh i x 

i l l l sin  sinh l l 

i i



Trên hình 4.14c cho ta dạng dao động riêng cơ bản và dạng dao động riêng bậc l.

Giải bằng số phương trình đặc trựng (3.34) ta được

EI

l4

 1,875  3,516

1 1

EI

l4

(3.37)

 4, 694  22, 034

2 2

Biểu thức nghiệm tổng quát (3.29) trong trường hợp này có dạng

𝑘=1

𝑤 𝑥, 𝑡 = ∞ 𝑋𝑖 (𝑥) 𝐴𝑖 cos 𝜔𝑖 𝑡 + 𝐵𝑖 sin 𝜔𝑖 𝑡 (3.38)

Các hằng số Ai , Bi được xác định từ các điều kiện đầu

wx,0w

x,

w(x,0)v

(x)

0

Như thế, ta có

t 0

∞

𝑖=1

𝑋𝑖𝑥 𝐴𝑖 = 𝑤0𝑥 , ∞

𝜔𝑖 𝑋𝑖𝑥 𝐵𝑖 = 𝑣0𝑥

𝑖=1

Nhân hai vế của các phương trình trên với hàm riêng Xk(x) rồi lấy tích phân theo x từ 0 đến l. Chú ý đến tính chất trực giao của các hàm riêng, ta được

1 1

Ak 

w0 xX k xdx;

Bk 

v0 xX k xdx;

0

0

1

1

X 2 xdx X 2 xdx

0k 0k

Tiến hành tính toán tương tự, ta xác định được các phương trình đặc trưng, các tần số riêng và các hàm riêng của bài toán dao động uốn tự do của dầm với các điều kiên biên khác nhau. Bảng 4.2 cho ta biết phương trình đặc trưng, các trị riêng của một số mô hình dao động uốn của dầm hay gặp.

Thí dụ 4.7: Cho dầm đồng chất, thiết diện không đổi, đầu bên trái ngàm chặt, đầu bên phải tự do mang khối lượng m. Cho biết =m/l = 3/4. Hãy xác định các tần số riêng cơ bản và các tần số riêng bậc l (hình 4.15).

El

x

l

m

w(l,t)

Q(l,t)

m

z z

a) b)

Hình 4.15 Hình thí dụ 4.7

Lời giải: Cũng giống như trường hợp dầm bị ngàm chặt một đầu, một đầu ự do ở trên ta có ba điều kiện biên

w(0,t)=0 w’(0,t)=0 M(l,t)=-EIw’’(l,t) =0

Để tìm điều kiện biên thứ tư, ta tưởng tượng tách khối lượng m khỏi dầm (hình 4.15b), từ định luật Newton II đối với khối lượng m ta có

𝑚𝑤 𝑙, 𝑡 = −𝑄 𝑙, 𝑡 → 𝐸𝐼𝑤′′𝑙, 𝑡 − 𝑚𝑤 𝑙, 𝑡 = 0

Với các điều kiện biên trên, từ biểu thức nghiệm (3.20), (3.24), (3.27) ta có C1 + C3 = 0

C2 + C4 =0

- C1cos  - C2sin  + C3cosh  + C4sinh  =0 C1sin  - C2cos  + C3 sinh  + C4 cosh 

+ (C1cos  + C2sin  + C3cosh  + C4sinh )=0

Từ hai phương trình đầu ta suy ra C1=-C3 , C2 = - C4 . Thế vào hai phương trình sau ta được

- C1(cos  + cosh )- C2 (sin  + sinh  ) =0 C1 (sin  + cos  - sinh  -  cosh 

-C2 (cos  -sin  + cosh  + sinh ) =0

Từ điều kiện để cho C1 , C2 không đồng nhất triệt tiêu, ta nhận được phương trình đặc trưng

L + cosh  cos  + (sinh  cos  - cosh  sin  ) = 0 (3.39) Khi  = 3/4, giải phương trình trên bằng phương pháp số ta có

𝜆1

𝜆2

= 1,320 → 𝜔1

= 4,060 → 𝜔2

𝐸𝐼

= 1,742

𝜇 𝑙4

𝐸𝐼

= 16,48

𝜇 𝑙4

(3.40)

So sánh với kết quả (3.37) về các tần số riêng của dầm một đầu ngàm chặt, một đầu tự do ta thấy với khối lượng phụ m hai tần số riêng đầu tiên giảm đáng kể

2 EI

l2 

Phương trình đặc trưng	k	k
	coscosh - 1 = 0	1	4,730
		2	7,853
		3	10,996
		n	 (2n+1) π/2
	sin = 0	1	π
		2	2π
		3	3π
		n	nπ
	coscosh + 1 = 0	1	1,875
		2	4,694

			3 n	7,855  (2n-1) π/2
			tg - tgh = 0	1 2 3 n	3,927 7,069 10,210  (4n+1) π/4

Xem tất cả 182 trang.