Dao Động Dọc Tự Do Của Thanh Đồng Chất Tiết Diện Không Đổi

1 c ( y y* s )2 1 c ( y y* s )2

(3.70)

2 1 C 1 1 2 2 C 2 2

Thế các biểu thức động năng và thế năng vào phương trình Largrange loại II

d ( T ) T



(i = 1,2)

dt qiqi

qi

Ta nhận được phương trình vi phân dao động của ôtô

myc y c h(c

c cos t c

sin t)

C 11 C 12

2 11 13 14

J c y c h (c

c cos t c

sin t)

(3.71)

C 21 C 22

2 21 23 24

2

Trong các phương trình (3.71) ta ký hiệu c11 = c1 + c2 c21 = c12

c12 = c2s2 – c1s1 c22 = c1s12 + c2s2

c  c

 c cos 2l

c c s

 c s cos 2ππ

(3.72)

13 1 2 L 23 1 1 2 2 L

c14

c2

sin 2l

L

c24

c2 s2

sin 2l

L

Để tìm các tần số riêng ta xét hệ phương trình vi phân tuyến tính thuần nhất tương ứng với (3.72)

m0 yCc11 c12 yC0

 0 J

c

c 

0

C 

21

22 



Phương trình tần số có dạng

C 2M

Từ đó suy ra

c11

2m c21

c22

c12  0

C

2 J

4 2 c

m c J

c c

c2 

22 11 C

mJC

11 22 120

mJC

c m c J 

c m c J  4mJ 

2

c c c 

2

22 11 C

22 11 C

C 11 22 12

Giải ra ta được





2

1,2

2mJC

(3.73)

Ta tìm nghiệm riêng của hệ phương trình (3.73) dưới dạng yC = A0 + A1cosst + A2sint

 = B0 + B1cost + B2sint (3.74)

Thế các biểu thức (3.74) vào hệ phương trình vi phân (3.73) rồi so sánh cân bằng các hệ số ta nhận được các phương trình đại số tuyến tính để xác định các hằng số A0, A1, A2, B0, B1, B2.

c11A0 + c12B0 = hc11/2

c21A0 + c22B0 = hc21/2

(c11 - m2)A1 + c12B1 = -hc13/2

c21A1 + (c22 - JC2)B1 = -hc23 /2 (3.75) (c11 - m2)A2 + c12B2 = -hc14/2

c21A2 + (c22 - JC2)B2 = -hc24 /2

Giải ra ta được

A h ;

B  0

0 2

h c c

c c

J 2 

0

h c c

c c

J 2 

A1 

23 12

13 22 C ;

B1 

13 12

23 11 C

2

h c c



c c

J 2 

2

h c c



c c

J 2 

11

22

A2 2

24 12

14 22 C ;



B2 2

14 12

24 11 C

12



với

c

m2 c

JC

2 c2

Thế các hằng số A0, A1, A2, B0, B1, B2 tìm được vào biểu thức nghiệm (3.74) ta được các biểu thức xác định dao động cưỡng bức của ôtô

y h{11c c

c (c

J 2) cos t 

C 2 

23 12 13 22 C

(3.76)



1c c c (c J 2 ) sin t}

24 12 14 22 C

h c c

c (c

m2 )cos t c c

c (c

m2 )sin t

(3.77)

213 12

23 11

14 12

24 11

Hiện tượng cộng hưởng xảy ra khi  = I (i = 1,2). Từ biểu thức (3.69) ta suy ra vận tốc giới hạn của ôtô

v* L ω

(i = 1,2) (3.78)

i 2π i

Để minh hoạ hằng số ta lấy L = 0,15m; h = 0,05m; s1 = 1,6m; s2 = 2m; c1 = 245,1662 N/cm; c2 = 294,1995 N/cm; m = 600kg; JC = 600 kgm2. Từ các số liệu trên ta có

l  24  c14 = c24 = 0; c13 = c1 + c2 = c11; c23 = c2s2 – c1s1 = c12

L

Từ các công thức (3.73) ta tính được

1 = 9,22s-1; 2 = 17,48s-1;

Vận tốc tới hạn của ôtô là

v* L ω  0,22 m / s  0,7 km/ h

1 2π1

2

v* 

L

2π ω2

 0,43m / s 1,5 km/ h

Biểu thức nghiệm (3.76) bây giờ có dạng

c

h c2 c c c J 2 h





yC 

1

12 11 22

11 C

2

cos t

2

y0 cos t

2 c11

m2

c22

JC12  2

Đường cong cộng hưởng có dạng định tính như hình 3.14c.

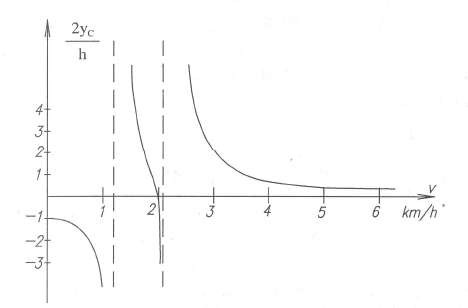
Hình 3.14c Đồ thị đường cong cộng hưởng

CÂU HỎI ÔN TẬP

x1

x2

c2 c2

m2

1. Cho mô hình dao động như hình vẽ, hãy thiết lập phương trình vi phân dao động của hệ.

x1

c1

x2

c2

c2

m1

m2

c1
	m1
c1

Có thể bạn quan tâm!

• Phương Pháp Giải Trực Tiếp (Ma Trận Cản Tùy Ý)
• Phương Pháp Ma Trận Dạng Riêng (Ma Trận Cản Đặc Biệt)
• A Mô Hình Dao Động Bộ Tắt Chấn Động Lực Có Tính Đến Ma Sát Nhớt
• Các Điều Kiện Biên Của Một Vài Dạng Liên Kết
• Thiết Lập Phương Trình Vi Phân Dao Động Uốn Của Dầm
• Dao Động Uốn Tự Do Của Dầm Euler- Bernoulli Đồng Chất Tiết Diện Không Đổi

Xem toàn bộ 182 trang tài liệu này.

x1

c1

x2

c2

x3

c3

m1

m2

m3

c 1
	m1

c2 c2
	m2

x1

x2

c 1

Hình 3.15 Hình bài tập 1

2. Thiết lập phương trình vi phân dao động nhỏ của cơ hệ có hai thanh đồng chất, khối lượng m, chiều dài L nối với nhau bằng lò xo có độ cứng c. Ở vị trí cân bằng các thanh thẳng đứng, lò xo không biến dạng.

O1

O2

L

1

2

a

Hình 3.16 Hình bài tập 2

3.Cơ cấu truyền động của máy tiện được mô hình thành hệ ba đĩa có mô men quán tính đối với trục quay x là J1, J2 J3. Ngẫu lực ma sát nhớt ở các ổ đỡ tỉ lệ với vận tốc góc. Các đoạn trục có độ cứng xoắn là c1, c2 và khối lượng không đáng kể. Mô men xoắn của động cơ truyền qua dây đai là M(t). Thiết lập phương trình vi phân dao động của cơ hệ.

1 1 1

			c1		c2
			M1		M2 M(t)

J1 J1 J1

Hình 3.17 Hình bài tập 3

4. Thiết lập phương trình vi phân dao động của dầm không trọng lượng mang ba khối lượng tập trung m1, m2, m3; mô đun đàn hồi của dầm là E, mômen quán tính của mặt cắt ngang là I.

F1

F2

F3

q1

q

2

q3

L/4 L/4 L/4 L/4

Hình 3.18 Hình bài tập 4

Chương 4

DAO ĐỘNG TUYẾN TÍNH CỦA HỆ VÔ HẠN BẬC TỰ DO

Các hệ liên tục còn được gọi là các hệ vô hạn bậc tự do. Trong chương này, ta xét dao động của một số hệ liên tục đơn giản nhưng hay gặp trong kỹ thuật. Đó là dao động của thanh và dầm. Các đại lượng vật lý đặc trưng cho dao động của hệ vô hạn bậc tự do như khối lượng, độ cứng phân bố một cách liên tục.

Phương trình mô tả dao động của hệ liên tục là các phương trình đạo hàm riêng.

Ở các hệ liên tục, ta nhận được vô số các tần số riêng, các dạng dao động riêng, vv…

4.1 DAO ĐỘNG DỌC VÀ DAO ĐỘNG XOẮN CỦA THANH THẲNG

4.1.1 Dao động dọc tự do của thanh đồng chất tiết diện không đổi

Xét một thanh thẳng (hình 4.1a) có mật độ khối là (x), thiết diện là A(x), môđun đàn hồi là E. Thanh thực hiện dao động (u,t) dọc trục (x). Áp dụng nguyên lý d’Alembert, xét một phân tố của thanh chịu lực như hình 4.1b. Phương trình chuyển động theo trục x của phân tố thanh có dạng

2u

N 

xAxdx t2

N N dx 

x



x A x 2

2u

t

N

x

(1.1)

Từ giáo trình sức bền vật liệu [37, 49] ta có

N EAxu

x

Thế biểu thức trên vào phương trình (1.1) ta nhận được phương trình dao động học tự do của thanh thẳng

2u u 

xAxt2x EAxx  0

(1.2)

Khi (x) và A(x) đều là các hằng số, từ phương trình (1.2) ta suy ra phương trình dao động dọc tự do của thanh thẳng đồng chất thiết diện không đổi

2u 

t2

2 2u

c x2

 0;

c2 E



dx

(1.3)

x

E,A

a)

N

dmAdx

b)

N+ dx

x

Hình 4.1 Thanh thẳng đồng chất tiết diện không đổi

Như thế phương trình dao động dọc tự do của thanh thẳng là phương trình đạo hàm riêng cấp hai. Bây giờ ta tìm nghiệm của phương trình (1.3) dưới dạng

u(x, t) = X(x)T(t) (1.4)

Thế biểu thức nghiệm (1.4) vào phương trình (1.3) ta có X(x)𝑇(t) – c2X”(x)T(t) = 0

''

c2 X x

X x

T&&(x) T (x)

Do vế trái của phương trình trên chỉ phụ thuộc vào x, còn vế phải chỉ phụ thuộc vào t, cho nên hai vê đó phải bằng hằng số. Với mục đích trước, ta ký hiệu hằng số đó là -2. Ta có

2

X '' x

c X x

T&&(x) 2

T (x)

Từ đó ta nhận được hai phương trình vi phân thường

2

X '' x

c 

X x 0

(1.5)

𝑇 𝑡 + 𝜔2 𝑇 𝑡 = 0 (1.6)

Nghiệm tổng quats của các phương trình này có dạng

X xA* cos x Bsin x

c c

(1.7)

T(t) = Ccos t + Dsin t (1.8)

x

l

Các hằng số A*, B được xác định từ các điều kiện biên, còn các hằng số C, D được xác định từ các điều kiện đầu.

x

l

E,A

E,A

E,A

x

l

a) b) c)

Hình 4.2 Liên kết thanh thẳng đồng chất tiết diện không đổi

Đối với thanh một đầu ngàm chặt, một đầu tự do (hình 4.2a), các điều kiện biên có dạng

u(0,t) = 0  X(0) = 0  A* = 0

N l,t EA u l,t  0 X l  0 B cos l  0

x c c

Với các giả thiết B ≠ 0,  > 0, ta suy ra phương trình đặc trưng



cos

l  0

c

(1.9)

Từ đó suy ra các tần số riêng và các hàm riêng

E

l2

2k l c 2k l ;

k  1, 2,(1.10)

k 2 l 2

X xB

sin 2k l x;

k  1, 2,

k k 2 l

Đối với thanh hai đầu bị ngàm chặt (hình 4.2b), các điều kiện biên có dạng X(0)=0  A* = 0; X(l)=0

Từ đó suy ra các tần số riêng và các hàm riêng

k ck

k l

E;

l2

X k xBk

sin kx;

l

(1.11)

Đối với thanh hai đầu tự do (Hình 4.2c), các điều kiện biên có dạng

X’(0)=0  B = 0; X’(l) = 0 

Từ đó ta nhận được

sin l  0

c

E

l2

k ck; X xA* cos kx

(1.12)

k l k k l

Như thế, từ các điều kiện biên, chúng ta xác định được các tần số riêng và hàm riêng. Bảng 4.1 thống kê một số dạng cơ bản các điều kiện bài toán dao động dọc thanh.

Thí dụ 4.2: Hãy xác định các tần số riêng và các hàm riêng của thanh một đầu bị ngàm chặt, một đầu mang khối lượng điểm m như hình 4.3a.

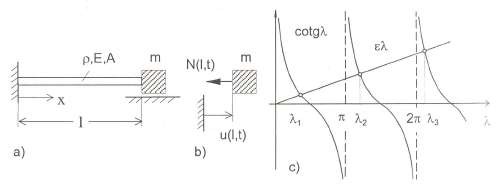
Hình 4.3 Hình thí dụ 4.2

Lời giải: Điều kiện bên trái

u(0, t) = 0  X(0) = 0  A* = 0

Điều kiện biên bên phải

EA u l,t 

x

m

2u l,t 

t2

EAX ' l m2 X l 

EAB

cos l m2 Bsin l

c c c