Phương Pháp Ma Trận Dạng Riêng (Ma Trận Cản Đặc Biệt)

Thế biểu thức nghiệm (3.2) vào phương trình (3.1) rồi đơn giản đi thừa số eλ t , ta nhận được phương trình của bài toán giá trị riêng tổng quát

λ2𝐌 + λ𝐁 + C 𝐪 = 0 (3.3)

Điều kiện cần để cho các phần tử của véc tơ 𝒒 không đồng thời triệt tiêu là

𝑃 𝜆 = 𝑑𝑒𝑡 λ2𝐌 + λ𝐁 + C = 0 (3.4)

Phương trình (3.4) được gọi là phương trình đặc trưng. Khi M là ma trận chính qui, det M ≠ 0, thì P(λ) là đa thức bậc 2n của λ với hệ số thực. Giải phương trình (3.4) ta có được 2n nghiệm thực hoặc phức liên hợp. Trong đó nếu λi là nghiệm bội m thì xem m là nghiệm. Các trị riêng phức và thực của (3.3) có thể viết dưới dạng

λk = −δk + iωk , λk+s = −δk − iωk , k = 1, … , s ≤ n λk = −δk, k = 2s + 1, … ,2n

b, Phân tích các khả năng dao động theo các trị riêng

- Trường hợp trị riêng có phần thực âm khác không

Định nghĩa : Khi δk > 0 (k =1, …, s), δk > 0 (k = 2s+1, …, 2n) thì cản được gọi là đạt yêu cầu.

Khi cản đạt yêu cầu thì hệ thực hiện dao động tự do tắt dần. Hệ dao động là ổn định tiệm cận. Tùy theo tính chất của chuyển động của hệ, ta có thể phân ra thành ba trường hợp sau :

Có thể bạn quan tâm!

Xem toàn bộ 182 trang tài liệu này.

Cản yếu : s = n, ωk ≠ 0 (k = 1,…,n)

Cản mạnh: λk = -δk< 0, (k = 2s+1, …,2n), Cản hỗn hợp: trường hợp còn lại.

Trong trường hợp cản yếu, hệ thực hiện chuyển động dao động. Trong trường hợp cản mạnh, hệ thực hiện chuyển động tắt dần

- Các trường hợp khác:

Khi trị riêng λk có δk = 0 hoặc δk = 0, nghiệm riêng tương ứng với λk sẽ bị chặn. Hệ (3.1) ổn định giới hạn.

Khi phương trình (3.3) có trị riêng λk có phần thực dương thì nghiệm riêng tương ứng với λk sẽ tăng lên vô cùng khi t tăng. Hệ không dao động. Ta không xét trường hợp này.

c) Các véc tơ riêng

Ứng với trị riêng λk , từ hệ phương trình (3.3) ta có:

𝑘

(𝜆2 M + λk B + C) 𝐪 k = 0 (3.5)

Từ (3.5) ta xác định được các véc tơ riêng 𝐪 k. Nhe đã biết từ đại số tuyến tính, nếu nghiệm của phương trình (3.4) là nghiệm đơn hoặc nếu là nghiệm bộ mà bội đại số bằng bội hình học, thì các véc tơ riêng tương ứng sẽ độc lập tuyến tính.Ta có thể sắp xếp 2n trị riêng λk ứng với 2n véc tơ riêng. Các véc tơ riêng được xác định phức liên

hợp là các véc tơ phức, còn các véc tơ riêng ứng với các trị riêng thực là các véc tơ thực.

Các véc tơ riêng của hệ dao động tự do có cản nói chung không trực giao với ma trận khối lượng M, ma trận cản B và ma trận độ cứng C. Tuy nhiên, nếu giả sửa có tồn tại một trị riêng λk mà δk = 0. Khi đó ta có

λk = iωk , 𝜆k+s = -iωk (3.6)

k

k

Thế (3.6) vào phương trình (3.5) ta được (-ω2 M + i ωkB + C)q k= 0 (-ω2 M - i ωkB + C)q k= 0

Cộng hai phương trình trên ta được

k

(-ω2 M + C)q k= 0 , ωk Bq k= 0 (3.7)

Từ (3.7) ta suy ra q k là véc tơ riêng của hệ dao động tự do không cản. Khi M và

C là các ma trận đối xứng thì q k trực giao với M và C

d)Nghiệm tổng quát của bài toán doa động tự do có cản yếu

Trong trường hợp hệ có cản yếu, ta có

λk = -δk + iωk , 𝜆k+n = -δk - iωk , k = 1,…,n Trong trường hợp này ta đặt

q k= u k+ iv k, q k+n = u k- iv k

Nghiệm riêng tương ứng với cặp trị riêng λk và 𝜆k+n có dạng

𝐪k t = Ckeλkt 𝐮 k + i𝐯 k + Dkeλk +n t 𝐮 k − i𝐯 k(3.8) Với Ck,Dklà các hằng số phức. Nếu ta đưa vào các hằng số tích phân mới

Ck = Ck+Dk, Dk= i(Ck-Dk) Thì biểu thức (3.8) có dạng

𝐪kt = e−δk tCk𝐮k + Dk 𝐯 kcos ωk t + Dk 𝐮 k − Ck 𝐯 ksin ωk t (3.9)

Nghiệm tổng quát của phương trình dao động tự do có cản (3.1) có dạng

n

𝐪 t = 𝐪k (t)

k=1

Chú ý: Do u k và v k nói chung không tỷ lệ với nhau nên các tọa độ của véc tơ qk có pha khác nhau

3.3.2 Phương pháp ma trận dạng riêng (ma trận cản đặc biệt)

Trong một số bài toán kỹ thuật ma trận cản B có thể biểu diễn dưới dạng

B = αM + 𝛿C (3.10)

Trong đó α và 𝛿 là các hằng số. Ma trận (3.10) được gọi là ma trận cản Rayleigh. Biểu thức (3.10) có khi được viết dưới dạng

B = α ω M + β C



Trong đó ω là mọi tần số quy chiếu tùy ý được đưa vào để α và β là các đại lượng không thứ nguyên. Công thức cản Rayleigh có vai trò quan trọng trong động lực học công trình.

Khi đó bằng phép biến đổi q = Vp, với V là ma trận dạng riêng, ra đưa được phương trình (3.1) về dạng

µi p i + βi p i + γi pi = 0 (i=1,2,…,n) (3.11) Trong đó:

µ𝑖 = 𝑣𝑇 Mvi; βi = 𝑣𝑇 Bvi; γi =𝑣𝑇 Cvi (3.12)

𝑖 𝑖 𝑖

Nghiệm của các phương trình dạng (3.11) đã được khảo sát kỹ trong chương 2.

Chú ý: Việc đưa phương trình (3.1) về dạng (3.11) tương đương với việc đưa đồng thời 3 ma trận M, B, C về dạng đường chéo. Người ta đã chứng minh được định lý sau

Định lý: Điều kiện cần và đủ để hệ phương trình (3.1) đưa được về dạng vế trái tách rời nhau (3.11) là điều kiện hóa vị vị trí như sau:

BM-1C = CM-1B

Khi M, B, và C là các ma trận đối xứng, điều kiện trên có thể viết dưới dạng

BM-1C = (BM-1C)T

Trong một vài tài liệu người ta cũng đưa ra một vài dạng khác về điều kiện chéo hóa đồng thời ba ma trận M, B, và C. Tuy nhiên những kết quả này thường mang nặng ý nghĩa lý thuyết hơn thực hành.

Thí dụ 3.12: Cho mô hình dao động hệ hai bậc tự do như hình 3.11. Hãy tìm nghiệm của hệ bằng phương pháp ma trận dạng riêng.

Lời giải: Các biểu thức động năng, thế năng và hàm hao tán của hệ có dạng

T = 1 m(q 2 + q 2 )

2 1 2

П = 1cq2 + 1c(q – q )2 + 1cq2

2 1 2 1 2 2 12

12

Φ = b

2

q 1 − q 2

c

b

m

c

c

m

q1

q2

Hình 3.11 Hình thí dụ 3.12

Thế các biểu thức động năng, thế năng và hàm hao tán vào phương trình Lagrange loại II ta nhận được phương trình vi phân dao động tự do có cản của hệ

2

m 0 q 1

b −b

q 1

2c −c q1 0

0 mq

+ −b bq

+ −c 2cq2= 0

2

Chia phương trình trên cho m và sử dụng các ký hiệu

ω2 = c , δ = b , D = δ

0 m 2m ω0

ta được

1 0q 1+ 2ω D 1 −1q 1+ ω22 −1q1= 0

0 1

Nếu chọn

q 2

0 −1 1

q 2

0 −1 2 q2 0

α = -2ω()

D; δ= 2D

ω0

thì từ phương trình trên ta có

B = αM + δC

Do đó ta có thể áp dụng phương pháp ma trận dạng riêng tìm nghiệm của phương trình dao động ở trên. Phương trình đặc trưng của hệ

2ω2 − λ2 −ω2

𝐂 − λ2𝐌 = 0 0= 0

−ω2 2ω2 − λ2

0 0

⇒ 𝜆4 − 4ω2λ2 + 3ω4

0 0

Giải ra ta được

λ2 = 3ω2; λ2 = ω2

1 0 2 0

Phương trình xác định các véc tơ riêng

(λ2 - 2ω2) a(i) + ω2) a(i) = 0

𝑖 0 1 0 2

1

Chọn a(i) = 1, ta có

(i) 2ω2 (1)

(2)

a =0

 a

= -1, khi λ2 = ω2 => a = 1

ω

2 2 2

i

1 0 2

Vậy ma trận dạng riêng là

V = 1 1

−1 1

Từ đó dễ dàng tính được

VTMV = 2 0, VTCV = ω26 0, VTCV = 2𝜔0D 4 0,

0 2 0 0 6 0 0

Phương trình dao động của hệ dưới dạng tọa độ chính

0

p 1 + 4ω0Dp 1 + 3ω2p1 = 0

0

p 2 + ω2 p2 = 0

Từ đó suy ra các biểu thức nghiệm dạng tọa độ chính

p1t= e−2Dω0 tC11 cos 3 − 4D2ω0t + C12 sin 3 − 4D2ω0t p2t = C21 cos ω0t + C22 sin ω0 t

Trở lại tọa độ suy rộng ban đầu ta có

q t p t p

t e2Dω0tC cos 3 4D2ω t  C sin 3 4D2ω t 

1 1 2

11 0 12 0 

C21 cos ω0t  C22 sin ω0t

q tp t p

te2Dω0tC cos 3 4D2ω t  C sin 3 4D2ω t 

2 1 2

11 0 12 0 

C21 cos ω0t  C22 sin ω0t Giả sử cho biết điều kiện đầu

q1(0) = q2(0) = 0, q 1(0) = v,q 2(0) = 0

Với các điều kiện đầu đó ta dễ dàng tính được C11 = C21 = 0

2ω0

3  4D2

C  v 1

,C v

12 22

2ω0

Nghiệm riêng ứng với các điều kiện đầu trên có dạng

v

q1t =

2ω0

1

3 − 4D2

e−2Dω0t sin3 − 4D2 ω0

t + sin ω0t

v

q2t = −

2ω0

1

3 − 4D2

e−2Dω0t sin3 − 4D2ω0

t − sin ω0t

3.4 Dao động cưỡng bức

3.4.1 Phương pháp giải trực tiếp

a) Dao động cưỡng bức không cản chịu kích động điều hoà

Dao động tuyến tính cưỡng bức không cản của hệ n bậc tự do chịu kích động điều hoà có dạng:

Mq&&Cq 

fˆ sin t

(3.13)

Ở chế độ chuyển động bình ổn, ta tìm nghiệm phương trình (3.13) dưới dạng q(t) = u sint (3.14)

Thế (3.14) vào (3.13) ta suy ra

(2M C)u fˆ

u H () fˆ

(3.15)

Trong đó:

H ()  (2M C)1 và được gọi là ma trận chuyển

Giải hệ phương trình đại số (3.15) ta được

u () k ()

k ()

(3.16)

Trong đó: () = det(-2M + C) (3.17)

k() có được bằng cách thay vec tơ fˆ vào cột thứ k của . So sánh (3.17) với

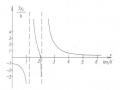
(2.4) trong cùng chương này ta thấy () = 0 khi  = j (j = 1, 2, …, n). Ta phân biệt ba trường hợp sau:

Trường hợp 1: () = 0; k()  0

Khi đó tần số lực kích động  trùng với một trong các tần số dao động riêng. Biên độ dao động tăng lên vô cùng. Trường hợp này được gọi là trường hợp cộng hưởng.

Trường hợp 2: () = 0;  = j

k() = 0 với mọi k và

lim

j

k () 

()

Trong trường hợp này mặc dù tần số lực kích động trùng với tần số riêng nhưng biên độ dao động vẫn bị giới nội. Trường hợp này được gọi là trường hợp giả cộng hưởng.

Trường hợp 3: ()  0; k() = 0 với k xác định

Trong trường hợp này uk = 0. Dao động ứng với toạ độ thứ k bị dập tắt.

b) Dao động cưỡng bức có cản chịu kích động tuần hoàn

Về mặt toán học dao động cưỡng bức có cản nhớt của hệ tuyến tính n bậc tự do được mô tả bởi phương trình vi phân dạng ma trận như sau:

Mq&&Bq&Cq 

f (t)

(3.18)

Trong đó M, B, C là các ma trận hằng số; f(t) là vec tơ cột các ngoại lực tác dụng. Giả sử f(t) là véc tơ tuần hoàn theo thời gian và có thể khai triển thành chuỗi Fourier một cách gần đúng:

m

f (t) a0(akcos kt bksin kt)

k 1

(3.19)

Ta sử dụng nguyên lý cộng tác dụng trong lý thuyết hệ phương trình vi phân tuyến tính để tìm nghiệm phương trình (3.18). Trước hết ta tìm nghiệm phương trình

Mq&&0Bq&0Cq0a0

dưới dạng: q0 = v0.

Từ hai phương trình trên ta nhận được hệ phương trình xác định v0

Cv0 = a0 (3.20)

Sau đó ta tìm nghiệm của phương trình

Mq&&kBq&kCqkakcos kt bksin kt

Nghiệm của phương trình (3.21) được tìm dưới dạng: qk = uksinkt + vkcoskt

Đạo hàm véc tơ qk theo t

(3.21)

q&kk(ukcos kt  vksin kt)

2 2

q&&kk  (uksin kt  vkcos kt)

Thế các biểu thức của

qk, q&k, q&&k

vào phương trình (3.21) sồi so sánh các hệ số,

ta nhận được hệ phương trình đại số tuyến tính để xác định các véc tơ uk và vk.

C k 22M kB uk bk 

kB C k 22M v

a

(3.22)

k k 

Khi định thức của ma trận hệ số của hệ phương trình trên khác không, thì các véc tơ uk và vk được xác định duy nhất. Như thế nghiệm của phương trình dao động cưỡng bức (3.18) khi f(t) tuần hoàn được tính theo biểu thức:

m

q  v0(uksin kt  vkcos kt)

k 1

(3.23)

trong đó v0 được xác định từ phương trình (3.20), còn vk, uk được xác định từ phương trình (3.22).

3.4.2 Phương pháp ma trận dạng riêng

Phương pháp ma trận dạng riêng (Modalmatrix) được áp dụng thuận tiện đối với hệ tuyến tính không cản.

Mq&&Cq 

f (t)

(3.24)

trong đó M và C là các ma trận thực, đối xứng.

Áp dụng phép biến đổi toạ độ

q = Vp (3.25)

với V là ma trận dạng riêng, p là véc tơ các toạ độ chính, ta đưa được phương trình (3.24) về dạng:

MVq&&CVp 

f (t)

Nhân bên trái phương trình trên với ma trận chuyển vị VÉC TƠ của ma trận dạng riêng ta được.

V TMV&p&V TCVp V Tf (t)

(3.26)

Các ma trận VTMV và VTCV là các ma trận đường chéo có dạng như (2.26) Nếu ta đưa vào ký hiệu

h  vT f

(i = 1, 2, …, n) (3.27)

i i

Thì phương trình (3.26) được viết dưới dạng hệ n phương trình vi phân tuyến tính cấp hai

i&p&ipihi

(i = 1, 2, …, n) (3.28)

Trong đó i, i được xác định bởi công thức (2.28)

Nghiệm của mỗi phương trình của hệ (3.28) ứng với điều kiện đầu

pi(0) pi0 ; p&i(0) p&i0

theo công thức (5.16) chương 2 có dạng

p (t) p cost p&i0sin t 1

i i0 i i

t

hi ()sin i (t )d

(3.29)

Trong đó:

i

2 i

ii 0



i

i

Đối với trường hợp kích động điều hoà

fi (t) 

fˆ sin t

, theo công thức (327) ta có:

i

h (t) n

ˆ t hˆ sin t

i 

k 1

vki fk sini



Các phương trình (3.28) đối với trường hợp này có dạng:

i

i&p&iipihˆ sin t

(i = 1, 2, …, n) (3.30)

Nghiệm của các phương trình (3.28) trong giai đoạn bình ổn là

hp  sin t

ˆ

i

i

2 

i 12 

i 

Trở về toạ độ ban đầu qk ta có

n n vhˆ

qk(t) vki pi ki i sin t

(3.31)

i1

i1 2 

i 12 

i 

Như thế, khi chịu kích động điều hoà, hệ dao động với tần số của lực kích động và dạng dao động phụ thuộc vào các tham số của hệ và tần số của lực kích động ngoài. Từ công thức (3.31) ta thấy: khi tần số kích động  bằng tần số riêng i của hệ, biên độ dao động cưỡng bức tăng lên vô hạn. Hiện tượng đó được gọi là hiện tượng cộng hưởng.

Nếu kể đến lực cản tỷ lệ bậc nhất với vận tốc, phương trình vi phân dao động cưỡng bức có dạng:

Mq&&Bq&Cq 

f (t)

(3.32)

Trong kỹ thuật ta hay gặp trường hợp B = M + C

với ,  là các hằng số thực. Tương tự các mục trước, bằng phép biến đổi (3.25) phương trình (3.32) được đưa về dạng:

i&p&iip&iipihi(t)

(i = 1, 2, …, n) (3.33)

..... Xem trang tiếp theo?
⇦ Trang trước - Trang tiếp theo ⇨

Xem tất cả 182 trang.

Ngày đăng: 28/06/2022