Biểu Thức Của Mômen Động Lượng Của Vật Rắn Quay

dv d 

const, ta có:

F ma m

dt

 (mv )

dt

Đó là điều cần chứng minh.

Định lý 2: Đạo hàm theo thời gian động lượng của cơ hệ bằng véc tơ chính của hệ ngoại lực tác dụng lên cơ hệ.

dQe

dt Fk

Có thể bạn quan tâm!

• Điều Kiện Cân Bằng Và Các Phương Trình Cân Bằng Của Hệ Lực
• Định Luật 2 (Định Luật Cơ Bản Của Động Lực Học)
• Các Đặc Trưng Hình Học Của Cơ Hệ Và Vật Rắn
• Biểu Thức Động Năng Của Vật Rắn Chuyển Động
• Vật Quay Xung Quanh Một Trục Cố Định Với Vận Tốc 
• Phương Pháp Mặt Cặt Biến Thiên- Các Thành Phần Nội Lực Trên Mặt Cắt Ngang

Xem toàn bộ 180 trang tài liệu này.

(3.42)

F

k

Chứng minh: Đối với chất điểm Mk thuộc cơ hệ, chịu tác dụng của ngoại lực e

và nội lực

F i , theo định lý 1 ta có:

k

d e i

(m v ) F dt k k k

Fk

Lấy tổng hai vế với chú ý rằng véc tơ chính của hệ nội lực bằng không, ta được:

d d

dQ e

dt mkvkdt mkvk

Đó là điều cần chứng minh.

dt Fk

Định lý 3: Biến thiên động lượng của chất điểm trong một khoảng thời gian nào đó bằng xung lượng của lực tác dụng lên chất điểm trong khoảng thời gian đó.

t1 

mv1 mv0 Fdt

t0

Chứng minh. Từ (3.41) ta có:

v

d(m) Fdt

(3.43)

Khi tích phân hai vế của đẳng thức này với các cận tương ứng, ta được:



v1 t1 



d (mv ) Fdt

v0 t0

t1 

Vậy:

mv1 mv0 Fdt

t0

Đó là điều cần chứng minh.

Định lý 4: Biến thiên động lượng của cơ hệ trong một khoảng thời gian nào đó bằng tổng xung lượng của các ngoại lực tác dụng lên cơ hệ trong khoảng thời gian đó:

t1 

Q Q F edt S e

(3.44)

1 0 k k

t0

Chứng minh: Từ (3.42) ta có:

dQ F edt

k

Tích phân hai vế của đẳng thức trên với các cận tương ứng ta nhận được:





Q1 

dQ 



Q0

t1 t1

e 

Fk dt 

t0 t0



k

F edt

t1 

Hay: Q Q F edt S e

1 0 k k

t0

Đó là điều cần chứng minh.

Trong hệ trục toạ độ Đề các, các định lý vừa phát biểu trên được biểu diễn trong dạng (chúng ta chỉ trình bày đối với trường hợp cơ hệ, còn đối với trường hợp của chất điểm hoặc được suy ra bằng cách tương tự hoặc xem như là trường hợp riêng của cơ hệ):

dQ

F e 

dt x

d dt Qy

kx 





Fe

ky 



(3.45)

dQ

F e 

dt

Q1x Q1y

z

Q0 x

Q0 y

kz 



S e 

kx 

ky

S e 

(3.46)

Q Q 

S e 

1z 0 z

kz 

Chú ý: Nội lực không có mặt trong các định lý động lượng của cơ hệ. Từ đó suy ra rằng nội lực không làm biến đổi động lượng cơ hệ.

Định lý động lượng cho phép tìm được các tích phân đầu của chất điểm và của cơ hệ trong một số điều kiện của lực tác dụng. Nó cũng được sử dụng có hiệu quả cho bài toán va chạm và bài toán chuyển động của môi trường liên tục.

4. Định lý bảo toàn động lượng

Dưới đây chúng ta chỉ xét cho trường hợp cơ hệ. Đối với chất điểm được xem như là trường hợp đặc biệt của cơ hệ.

Định lý 5: Nếu véc tơ chính của các ngoại lực tác dụng lên cơ hệ luôn bằng không thì động lượng của cơ hệ được bảo toàn, tức:

k

F e  0

thì Q const

(3.47)

k

Chứng minh: Nếu F e  0

thì từ (3.42) ta có:



dQ

0

Tức là: Q const

dt

Đó là điều cần chứng minh.

Định lý 6: Nếu tổng hình chiếu các ngoại lực tác dụng lên cơ hệ trên một trục cố định nào đó luôn luôn bằng không thì hình chiếu của động lượng cơ hệ trên trục đó được bảo toàn.

kx

x

F e 0 thì Q

const

(3.48)

kx

Chứng minh: Nếu Vậy: Qx const

F e 0 , từ (3.45) ta có:

dQx  0

dt

Định luật bảo toàn động lượng là cơ sở lý thuyết của cơ học vật có khối lượng biến đổi, đặt nền tảng cho ngành cơ học du hành vũ trụ.

3.3.1.2. Định lý chuyển động khối tâm cơ hệ

Định lý: Khối tâm của cơ hệ chuyển động như một chất điểm có khối lượng bằng khối lượng của cơ hệ và chịu tác dụng của lực có véc tơ lực bằng véc tơ chính của hệ ngoại lực tác dụng lên cơ hệ:

e

MaCFk

(3.49)

Chứng minh: Áp dụng định lý động lượng dạng đạo hàm (3.42 ta nhận được:

dQd

e

(MvC ) MaC Fk

dt dt

Đó là điều cần chứng minh.

Vì phương trình vi phân chuyển động khối tâm (3.49) có dạng phương trình cơ bản của động lực học chất điểm, nên có thể viết phương trình (3.49) trong các dạng toạ độ khác nhau. Ví dụ phương trình vi phân chuyển động khối tâm có thể viết trong dạng toạ độ Đề các:

MxCMyCMzC

F e

kx

ky

F e

kz

F e

(3.50)

Từ định lý trên suy ra nội lực không ảnh hưởng đến chuyển động của khối tâm, dù rằng nội lực có ảnh hưởng đến chuyển động của từng bộ phận cơ hệ.

Định luật bảo toàn chuyển động khối tâm.

Từ công thức (3.49) ta thấy rằng:

Nếu

F e

k



 0 thì 

 0

aC



Tức là: vC const

Vậy:

hoặc vC  0

(3.51)

Nếu véc tơ chính của các ngoại lực tác dụng lên cơ hệ luôn luôn bằng không thì khối tâm của cơ hệ hoặc đứng yên hoặc chuyển động thẳng đều.

F

Đó là định luật bảo toàn chuyển động khối tâm. Tương tự, nếu:

e kx

Vậy:

 0 thì

xC

 0 , tức là

xC

const

hoặc

xC 0

(3.52)

Nếu tổng hình chiếu của các ngoại lực tác dụng lên một trục cố định nào đó

luôn luôn bằng không thì hình chiếu của khối tâm của cơ hệ lên trục đó hoặc đứng yên hoặc chuyển động thẳng đều.

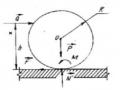
Ví dụ 3.4. Trục quay của động cơ được mô hình bằng khối lượng m2 cách tâm trục quay khoảng e.

m2

t

O

P2

P1

N

Giả sử trục động cơ quay đều với vận tốc góc .

Vỏ mô tơ có khối lượng m2. Hãy xác định:

- Phương trình chuyển động ngang của vỏ mô tơ trên nền nhẵn.

- Áp lực thẳng đứng của động cơ tác dụng lên nên ngang.

Bài giải

Khảo sát chuyển động cơ hệ gồm vỏ mô tơ, rô to và khối lượng lệch tâm.

Các ngoại lực tác dụng lên cơ hệ gồm: (P1, P2, N )

Trong đó: N : Phản lực của nền lên động cơ. (Hình 3.12)

Hình 3.12

Các ngoại lực đều song song với phương thẳng đứng, nên theo định lý bảo toàn chuyển động của hình chiếu khối tâm lên trên trục nằm ngang, ta có:

xC = const = 0 (Vì ban đầu hệ nằm yên) Theo công thức tính toạ độ khối tâm, ta có:

C

x m1 x1 m2 x2 m1 x1 m2 (x1 e cost)  0

m1 m2 m1 m2

Từ đó: x1

m2e m m

cost

1 2

Như vậy vỏ của động cơ dao động điều hoà với biên độ a và chu kỳ T:

a m2e m1 m2

, T 2



Để tìm phản lực N ta viết phương trình vi phân chuyển động của khối tâm theo trục thẳng đứng hướng lên Oy, ta có:

(m1m2)yCN P1P2

Vậy:

N  (m1m2)( yCg)

Trong đó: g là gia tốc trọng trường.

Theo công thức tính toạ độ khối tâm, ta có:

y m1 y1 m2 y2

m1.0 m2 .e cost 

m2e

cost

C m m

1 2

Vậy:

m1 m2

m1 m2

y

m e2



C

2cos t

m1 m2

Thay kết quả nhận được vào biểu thức của phản lực N đã tìm ở trên, ta nhận được:

N  (m

m )( y

g)  (m

m e2



m

1 2

m )(g 2 cos t)

1 2 C

1 m2

Như vậy phản lực N biến đổi theo thời gian, nó đạt trị số lớn nhất và bé nhất, đó là:

m e2

N  (m m )(g 2 )

max 1 2

m1 m2

N  (m

m e2

m )(g 2 )

min 1 2

m1 m2

Để động cơ không rời khỏi nền cần phải thoả mãn điều kiện: Nmin > 0, tức là:

m e2

g 2  0

(m1 m2 )g

m2e

m1 m2

Vậy:

2 

Nếu điều kiện này không thoả mãn thì động cơ sẽ rời khỏi nền và gây ra hiện tượng va đập giữa động cơ và nền.

3.3.2. Định lý mômen động lượng

3.3.2.1. Mômen động lượng

Mômen động lượng của chất điểm đối với tâm O là đại lượng véc tơ, được ký

hiệu bởi

Lo , là mômen của véc tơ động lượng chất điểm đối với tâm O:



Lo mo (mv) r mv 

i x mx

j y my

k z mz

(3.53)

Mômen động lượng của chất điểm đối với trục z là mômen của véc tơ động lượng chất điểm đối với trục z:

Lz mz (mv) (3.5)

Nếu gọi

Loz

là hình chiếu của Lo

lên trục Oz thì từ định lý liên hệ giữa mômen

lực đối với điểm và mômen lực đối với một trục trong phần tĩnh học, ta rút ra:

Lz Loz m(xyyx) (3.55)

Mômen động lượng của cơ hệ đối với một tâm bằng tổng mômen động lượng của các chất diểm của cơ hệ đối với cùng tâm đó.



Lomo (mkvk) rkmkvk

(3.56)

Mômen động lượng của véc tơ hệ đối với một trục bằng tổng mômen động

lượng các chất điểm của cơ hệ đối với cùng trục đó.

Lz mz(mkvk)

(3.57)

Đơn vị của mômen động lượng là

3.3.2.2. Định lý mômen động lượng

kgm2 / s

Định lý: Đạo hàm theo thời gian của mômen động lượng của chất điểm đối với một tâm (đối với một trục) cố định bằng tổng mômen của lực tác dụng lên chất điểm đối với cùng tâm (đối với cùng trục) ấy.

d Lo mo (F )

dt

d Lz m x (F )

dt

(3.58)

(3.59)

Chứng minh: Xét chất điểm M, có khối lượng m, chịu tác dụng của lực F (nếu

chịu tác dụng của nhiều lực thì F là hợp lực của các lực đó). Ta viết phương trình cơ bản của động lực học chất điểm trong dạng:

d (mv) F dt

Nhân hữu hướng hai vế của đẳng thức này với véc tơ định vị r của chất điểm, ta có:



r

r d (mv)

dt

F

Vế trái của đẳng thức với chú ý:

d r mv v mv  0

dt

Có thể viết như sau:

Do đó:

r d (mv) 

dt

d (r mv) dt

d 

(r mv) r F

dt

tức

d Lo mo (F )

dt

Đó là điều cần chứng minh.

Chiếu 2 vế của đẳng thức (3.58) lên trục

z đi qua O ta sẽ có biểu thức (3.59)

Định lý: Đạo hàm theo thời gian của mômen động lượng của cơ hệ đối với một tâm (một trục) cố định bằng tổng mômen của các ngoại lực đối với cùng tâm (cùng trục) đó:

d Lo dt

d Lz dt

mo

mz

k

(F e )

k

(F e )

(3.60)

(3.61)

Chứng minh: Xét chất điểm M k

của cơ hệ có khối lượng mk

chịu tác dụng của

ngoại lực

F e và nội lực

k

F i . Viết công thức (3.59) cho chất điểm

M k trong đó thay

k

F

k

k

thế lực F bằng hợp lực của e và F i , ta có:

d Lok mo (F e F i ) mo (F e ) mo (F i )

dt k k k k

Lấy tổng hai vế của bất đẳng thức với chú ý là mômen chính của hệ nội lực bằng không, tức là:

k

mo (F i) 0

ta có:

d Lok mo (F e)mo (F i)mo (F e)

dt

vậy:

k k k

d Lok d Lo mo (F e)

dt dt k

Đó là điều cần chứng minh.

Khi chiếu hai vế của đẳng thức (3.60) lên trục cố định qua O ta nhận được ngay đẳng thức (3.61).

Từ định lý nêu trên ta có nhận xét: các nội lực không làm biến đổi mômen động lượng của cơ hệ, mặc dù chúng làm biến đổi mômen động lượng của các bộ phận thuộc cơ hệ.

3.3.2.3. Định luật bảo toàn mômen động lượng

Dưới đây ta thiết lập định luật bảo toàn mômen động lượng cho cơ hệ, nhưng chúng cũng áp dụng được một cách dễ dàng cho trường hợp chất điểm, vì chất điểm được xem như một cơ hệ đặc biệt:

Từ (3.60) và (3.61) ta thấy:

nếu

mo

k

(F e )  0 thì

d Lo dt



 0 ; tức

Lo const

(3.62)

và nếu

k

mz (F e) 0 thì

d L z 0 ;tức

dt

Lz const

(3.63)

Vậy ta có định lý sau:

Định lý: Nếu tổng mômen có ngoại lực tác dụng lên cơ hệ đối với một tâm (một

trục) cố định luôn luôn bằng không thì mômen động lượng của cơ hệ đối với tâm (trục) đó sẽ không đổi.

Áp dụng định lý bảo toàn mômen động lượng cho chất điểm chuyển động dưới tác dụng lực F luôn luôn đi qua điểm cố định O (lực xuyên tâm), ta dễ dàng đi đến kết luận là chất điểm luôn luôn chuyển động trong mặt phẳng cố định chứa tâm O và vận tốc đầu của chất điểm. Ví dụ về trường hợp này là chuyển động của các hành tinh trong thái dương hệ (bỏ qua lực tác dụng tương hỗ giữa các hành tinh).

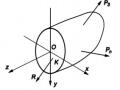
3.3.2.4. Áp dụng vào vật rắn z



mkvk

hk

vk

1. Biểu thức của mômen động lượng của vật rắn quay

quanh trục cố định đối với trục quay của nó

Ta có công thức sau đây:

L I .(3.64)

z z

trong đó là vận tốc góc của vật, I z

tính của vật rắn đối với trục quay.

là mômen quán

Lấy một phần tử M k

của vật rắn, có khối lượng

mk , nằm

cách trục quay một đoạn

hk . Do vận tốc của chất điểm hướng

thẳng góc với bán kính quay hk , thuận chiều quay của vật, có

Hình 3.13

giá trị bằng hk , nên động lượng của chất điểm, tức là

mk vk

B

F1

R

B



FN

F2

F3

RA

A

nằm trong mặt phẳng thẳng góc với trục quay và cách trục quay z

một đoạn

h ( m v cũng thẳng góc với bán kính quay h ), có

k k k k

mômen đối với trục quay cùng dương hay cùng âm theo , tức (Hình 3.13):

m (m v ) m h2

z k k k k

Vậy mômen động lượng của vật rắn đối với trục quay z ,

ký hiệu bởi

Lz , bằng:

L m (m v ) m h2  (m h2 )I 

z z k k k k k k z

2. Phương trình vi phân chuyển động của vật rắn quay quanh một trục cố định

Hình 3.14

Khảo sát một vật rắn quay quanh một trục cố định dưới tác dụng của các lực

hoạt động

F1,...,FN.

Các ngoại lực tác dụng lên vật rắn gồm các lực hoạt động

F1, F2 ,...., FN

và các lực liên

kết tại các ổ trục R A

và R B

(Hình 3.14)

Vì các phản lực ổ trục

RA , RB

có mômen đối với trục quay bằng không và