Các Đặc Trưng Hình Học Của Cơ Hệ Và Vật Rắn

Việc phân loại lực theo cách nào sẽ tuỳ thuộc vào phương pháp được dùng để khảo sát cơ hệ.

3.2.1.3. Các đặc trưng hình học của cơ hệ và vật rắn

1. Khối tâm của cơ hệ

Khảo sát cơ hệ gồm N chất điểm: M1, M2,…, MN có khối lượng tương ứng: m1,

m ,…, m . Vị trí của các chất điểm được xác định bằng các véc tơ định vị: .

2 N r1, r2 ,...,rN

(Hình 3.4).

Khối tâm của cơ hệ là điểm hình học C, vị trí của nó được xác định bởi công thức (3.10).

N 

mk rk

Có thể bạn quan tâm!

• Hệ Lực Cân Bằng Khi Véc Tơ Chính Và Mô Men Chính Triệt Tiêu
• Điều Kiện Cân Bằng Và Các Phương Trình Cân Bằng Của Hệ Lực
• Định Luật 2 (Định Luật Cơ Bản Của Động Lực Học)
• Biểu Thức Của Mômen Động Lượng Của Vật Rắn Quay
• Biểu Thức Động Năng Của Vật Rắn Chuyển Động
• Vật Quay Xung Quanh Một Trục Cố Định Với Vận Tốc 

Xem toàn bộ 180 trang tài liệu này.

rC k 1

M

N

(3.10)

Trong đó

M mk

k 1

được gọi là khối lượng của cơ hệ.

Trong hệ trục toạ độ Đềcác Oxyz, các toạ độ của điểm C được xác định bởi công thức:

xmk xk ;

C M

ymk yk ;

C M

zmk zk C M

(3.11)

Trong đó: xk, yk, zk là toạ độ của chất điểm Mk.

z

M2(m2)

M1(m1) C

r2 r1

r1 rk

O

x

Hình 3.4

M3(m3)

Mk(mk) y

Từ công thức (3.10) hoặc (3.11) suy trực tiếp rằng đối với các vật rắn nằm gần

k

M

k

O

y

quả đất thì khối tâm trùng với trọng tâm của chúng. z

Các công thức (3.10) hoặc (3.11) có thể áp dụng được

rk

cho trường hợp cơ hệ gồm nhiều vật rắn, trong đó mk vàlần

lượt là khối lượng và véc tơ định vị khối tâm của các vật rắn.

2. Mô men quán tính của vật rắn

a. Định nghĩa

* Mô men quán tính của vật rắn đối với trục z, ký hiệu x

Hình 3.5

Iz, là đại lượng vô hướng, được xác định theo công thức:

z

k

k

I m 2

(3.12)

Trong đó k

(Hình 3.5).

là khoảng cách đến trục z của chất điểm Mk có khối lượng mk

Khi đưa vào hệ trục toạ độ Oxyz, dễ dàng chứng minh rằng

z

k

k

k

I m (x2 y2 )

(3.13)

Tương tự:

I m ( y2 z2 )

(3.14)

x

k

k

k

y

k

k

k

I m (x2 z2 )

Trong đó: xk, yk, zk là các toạ độ của chất điểm Mk.

* Mômen quán tính tích Ixy, Iyz, Izx là những đại lượng được xác định theo các công thức sau:

Ixy mk xk yk ;

Iyz mk yk xk ;

Izx mk zk xk

(3.15)

* Mômen quán tính của vật rắn đối với điểm O:

k k

O

I m r 2

(3.16)

Trong đó: là véc tơ định vị của chất điểm M .

rk k

Dễ dàng chỉ ra các tính chất sau:

Ixy = Iyx; Ixz = Izx; Izy = Iyz (3.17)

I 1 (I

O 2x

I y

I z )

(3.18)

Trong kỹ thuật người ta đưa ra đại lượng bán kính quán tính của vật rắn đối với

trục z, ký hiệu là

z được xác định theo công thức sau:

z

2 I z

M

(3.19)

Đơn vị của mômen quán tính là kgm2, đơn vị của bán kính quán tính là m.

b. Mômen quán tính của một số vật đồng chất

* Thanh đồng chất có chiều dài l, khối lượng M.

mk

B

? xk y

xk

y

A

Hình 3.6

l

2

I Ay x dx 

0

l3

3

M l 2

3

(3.20)

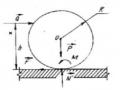
* Vòng tròn đồng chất, hình trụ vỏ mỏng có khối lượng M bán kính R (Hình 3.7).

I I 1 I 

x y 2 z

MR2

2

(3.21)

* Tấm tròn đồng chất, khối trụ đặc có khối lượng M bán kính R (Hình 3.8)

k

k

x

C

y

y

x

Hình 3.7 Hình 3.8

R

3

I z 2d

0

1 R4 

2

1 MR2

2

(3.22)

z

Hk

M

k





zk



O



yk

xk

y

x

Tương tự như trong trường hợp vòng tròn đồng chất:

Ta có:

I I 1 I 

Cx Cy 2 Cz

MR2

4

(3.23)

Công thức (3.23) cũng dùng để tính cho trường hợp khối trụ đặc.

Công thức tính mômen quán tính của các vật khác có thể tra cứu trong các sổ tay kỹ thuật.

c. Các định lý liên hệ mômen quán tính của vật rắn đối với các trục

Định lý 2: Định lý về mômen quán tính của vật rắn đối với trục đi qua gốc toạ độ (Hình 3.9).

y

z

yz

Mômen quán tính của vật rắn đối với trục bất kỳ qua gốc toạ độ có biểu thức:

Hình 3.9

II x

cos2 I

cos2 I

cos2  2I

coscos 2I zx

coscos

(3.24)

kiện:

 2I xy coscos

Trong đó: , , là ba góc chỉ phương của trục .

d. Các định lý về trục quán tính chính và trục quán tính chính trung tâm

Định nghĩa: Trục Oz được gọi là trục quán tính chính tại O nếu thoả mãn điều

Ixz = Izy = 0 (3.25)

Trục Oz được gọi là trục quán tính chính trung tâm nếu nó là trục quán tính chính và đi qua khối tâm.

Chú ý: Nếu hai trục là quán tính chính tại O thì trục thứ ba vuông góc với chúng cũng là trục quán tính chính.

3.2.2. Nguyên lý Đalămbe

3.2.2.1. Lực quán tính

Khi sát chất điểm dưới tác dụng của lực F chuyển động với gia tốc a đối với hệ quy chiếu quán tính nào đó. Theo định luật cơ bản của động lực học, ta có:

a

m F

a

Nó có thể được viết trong dạng:

F  (

m)  0

(3.26)

Đẳng thức (3.26) tương tự điều kiện cân bằng của chất điểm dưới tác dụng của



lực F và lực được gọi là lực quán tính, có ký hiệu

F qt :

m

F qt a

Chú ý

(3.27)

1. Lực quán tính không phải là lực tác dụng vào chất điểm (lực tác dụng vào chất điểm chỉ là lực F ). Dựa vào định luật tác dụng và phản tác dụng có thể khẳng định rằng lực quán tính của chất điểm tự do là lực do chất điểm tác dụng vào vật (số đo của nó là F ), đã buộc nó chuyển động với gia tốc a .

2. Khái niện cân bằng vừa nêu ở trên chỉ có ý nghĩa hình thức vì lực F và không tác dụng lên cùng một chất điểm.

F qt

3. Lực quán tính được xác định khi biết được gia tốc. Như vậy trong bài toán thuận (bài toán thứ nhất của động lực học) lực quán tính được hoàn toàn xác định, còn trong bài toán ngược (bài toán thứ 2 của động lực học) lực quán tính là đại lượng chưa biết.

Trong hệ trục tọa độ Đềcác, lực quán tính được xác định qua các hình chiếu của nó trên các trục tọa độ.

x

F qt mx ;

F qt my ;

F qt mz

(3.28)

x

x

Trong hệ trục tọa độ tự nhiên, lực quán tính được phân tích thành các phần trên các trục tọa độ tự nhiên.

a

a

F qt

F t qt F n qt

(3.29)

Với

F t qt 

mt ;

F n qt

mn

(3.30)

t

a

a

, n

là các véc tơ gia tốc tiếp và gia tốc pháp của chất điểm.

3.2.2.2. Nguyên lý Đalămbe

1. Nguyên lý Đalămbe đối với chất điểm.

Tại mỗi thời điểm lực tác dụng vào chất điểm và lực quán tính của chất điểm cân bằng nhau

F F qt  0 (3.31)

Chú ý: Trong trường hợp của chất điểm không tự do, lực tác dụng vào chất điểm bao gồm cả phản lực liên kết R , tức là:

F R F qt  0 (3.32)

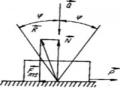
Ví dụ 3.2. Một quả cầu nhỏ có trọng lượng P được treo vào toa xe chuyển động thẳng với gia tốc a . Dây treo quả cầu bị lệch một góc α = cosnt so với đường thẳng đứng. Xác định gia tốc a của toa xe. (Hình 3.10).

a

T

Fqt

P

Hình 3.10

Bài giải

Khảo sát chất điểm chịu tác dụng của trọng lực và phản lực T của dây.

Lực quán tính của chất điểm, do gia tốc của chất điểm bằng gia tốc của toa xe, sẽ bằng:



F qt

m P 

a

a

g

Theo nguyên lý Đalămbe:

F T F qt  0

Chiếu hai vế của đẳng thức này lên phương vuông góc với dây ta có:

Fqtcosα – Psinα = 0

Nghĩa là

P a cosP sin  0

g

Vậy: a = g.tgα

Bài toán trên cho ta một phương pháp đơn giản để đo gia tốc của toa xe.

2. Nguyên lý Đalămbe đối với cơ hệ

Khảo sát cơ hệ gồm N chất điểm M1, M2,…, MN, dưới tác dụng của hệ lực

F , F ,...,F

chuyển động với gia tốc 

1 2 N

a1, a2 ,...,aN

Xét chất điểm Mk có khối lượng mk chịu tác dụng của lực Fk

chuyển động với

ak

gia tốc

. Lực quán tính của chất điểm ấy là

F qt 



m

k ak

Theo nguyên lý Đalămbe đối với chất điểm, với mọi chất điểm của cơ hệ ta có:

(Fk ' F k )  0

qt

Do đó nguyên lý Đalămbe đối với cơ hệ được phát biểu như sau:

Tại mỗi điểm, các lực tác dụng lên các chất điểm của cơ hệ và các lực quán tính của các chất điểm thuộc cơ hệ tạo thành hệ lực cân bằng.

(F , F ,....,F , F qt , F qt ,....F

qt )  0

(3.33)

1 2 n 1 2 N

3.2.2.3. Phương pháp Tĩnh hình học- Động lực

Nội dung phương pháp

Việc khảo sát điều kiện cân bằng của hệ lực có thể dựa vào hai đặc trưng hình học của nó là véc tơ chính và mômen chính của hệ lực. Dựa trên điều kiện triệt tiêu véc tơ chính và mômen chính của hệ lực ta thiết lập được phương trình cân bằng của hệ lực (trong phần Tĩnh học ta đã thiết lập các phương trình cân bằng đối với vật rắn).

Phương pháp thiết lập các phương trình cân bằng cho hệ lực (3.33) dựa vào tính chất triệt tiêu véc tơ chính và mômen chính của nó được gọi là phương pháp Tĩnh hình học- động lực.

Để áp dụng phương pháp này các lực tác dụng lên cơ hệ được phân thành những ngoại lực và những nội lực.

F F e F i

k k k

Vì véc tơ chính và mômen chính đối với một điểm bất kỳ của hệ nội lực luôn triệt tiêu, tức:

Ri F i 

i i

k 0; mO mO (Fk )  0

Nên phương trình cân bằng của hệ lực (3.33) có dạng sau:

F e F qt  0

(3.34)

k k

e qt

mO(Fk) mO(Fk

)  0

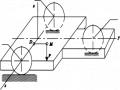
Ví dụ 3.3. Một trục máy mất cân bằng được mô hình bằng hai chất điểm M1, M2 có khối lượng tương ứng bằng m1, m2 nằm trong hai mặt phẳng vuông góc với nhau và chứa trục quay, khoảng cách của chúng đối với trục quay tương ứng bằng e1, e2. Trục máy quay đều với vận tốc 0. Xác định các phản lực tại ổ trục A và B. Các kích thước khác được cho như trên hình 3.11. Bỏ qua ma sát tại các trục quay.

Bài giải

Chọn hệ trục Axyz như hình vẽ

Khảo sát cơ hệ là trục máy gắn hai chất điểm M1, M2.

Các ngoại lực tác dụng vào cơ hệ: (P1, P2, X A, YA, ZA, XB, YB)

Các lực quán tính của hai chất điểm M1,

z

B

YB

X

B

e

M2

2

Fqt

2

P2

M1

e1

Z

A

A

P1

y

X

A

Y

A

M2 được ký hiệu bởi:

F qt, F qt

F qt 

1

với a

2

c

e .2

1

1 m1aM

M1 1 0

qt 

a e .2

F m a với M 2 0

2 2 M 22

b

Theo nguyên lý Đalămbe đối với cơ hệ

ta có:

(P , P , X , Y , Z , X , Y , F qt , F qt )  0

1 2 A A A B B 1 2

a

Hệ phương trình cân bằng tĩnh học cho

F qt

1

hệ lực trên như sau:1

Fx

X A

X B

F qt  0

Fy

YA

YB

F qt  0x

2

FzZ AP1P2 0

Hình 3.11

mx

(F) YB

(a b c) P2 e2

F qt (a b)  0

Hình 4.2

2

m (F) X

(a b c) P e F qt a  0

y B

mz(F)  0

1 1 1

Trong đó:

F qt P1 e 2 và F qt P2 e 2

1 g 1 0 2 g 2 0

Giải hệ phương trình trên ta được:

1 qt

Pe 2

X B 

(P1e1F1.a)  1 1 (1  0 a)

a b c a b c g

1 

qt

P e

2 

YB a b c

P2e2

F2 .(a b)

2 21



a b c 

0(a g

b)



1 

qt Pe



2 

X A a b c

P1e1

(b c)F1

1 11 (b a b c 

c)0

g 



1 

qt P e

2 

YA a b c

P2e2

cF2

2 21



a b c 

c0

g 

Z A P1 P2

Nhận xét: Các phản lực ở trục không những phụ thuộc vào vận tốc góc của trục

quay mà có phương thay đổi (các véc tơ máy với vận tốc góc 0).

RA và RB

quay quanh đường tâm của trục

3.3 CÁC ĐỊNH LÝ TỔNG QUÁT CỦA ĐỘNG LỰC HỌC CƠ HỆ

3.3.1. Định lý động lượng và định lý chuyển động khối tâm

3.3.1.2. Định lý động lượng

1. Động lượng

Động lượng của chất điểm là đại lượng véc tơ, ký hiệu là Q bằng tích của khối lượng chất điểm với véc tơ vận tốc của nó.

m



Q v (3.35)

Động lượng của cơ hệ bằng tổng động lượng của các chất điểm thuộc cơ hệ

Q 

m (3.36)

kv

k

Khi đạo hàm theo thời gian hai vế của đẳng thức véc tơ (2.1) ta có:





Do đó:

vC 

mk vk M

Q 



m

M

k v k vC

(3.37)

Tức động lượng của cơ hệ bằng động lượng của khối tâm với giả thiết khối tâm có khối lượng bằng khối lượng của cơ hệ.

Công thức (3.37) rất thuận tiện cho việc tính động lượng của vật rắn. Trong trường hợp hệ vật rắn, động lượng cơ hệ bằng tổng động lượng của các vật rắn.

Đơn vị của động lượng là: kgm/s

2. Xung lượng của lực (Xung lực)

Xung lượng nguyên tố của lực F , ký hiệu là

dS Fdt

dS , có biểu thức:

(3.38)

Xung lượng của lực F trong khoảng thời gian từ t0 đến t1 có biểu thức:

t1 

S Fdt

t0

Trong trường hợp lực không đổi (về độ lớn và hướng), tức

S F (t1 t0 )

(3.39)

F const , thì:

(3.40)

Đơn vị của xung lượng của lực (được gọi tắt là xung lực) là Ns.

3. Định lý động lượng

Định lý 1: Đạo hàm theo thời gian động lượng của chất điểm bằng lực tác dụng lên chất điểm đó



d (mv)

F

dt

(3.41)

Chứng minh: Khảo sát chất điểm M có khối lượng m chuyển động dưới tác dụng của lực F (trong trường hợp chất điểm chịu tác dụng của nhiều lực thì F là hợp

lực của các lực đó, tức

F Fk).

Khi viết phương trình cơ bản của động lực học cho chất điểm với chú ý là m =

Xem tất cả 180 trang.