Điều Kiện Cân Bằng Và Các Phương Trình Cân Bằng Của Hệ Lực

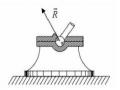
Có thể diễn tả khả năng chống lăn bằng cách dời song song phản lực pháp tuyến

N về phía bánh xe có xu hướng lăn đến một đoạn d = Ml / N (Hình 2.40b)

Ta có:

d Ml

kN k

N N

Vậy khi có ma sát lăn, phản lực pháp tuyến N nằm ở phía vật có xu hướng lăn đến và cách pháp tuyến một đoạn:

Có thể bạn quan tâm!

• Lực Liên Kết - Lực Hoạt Động - Phản Lực Liên Kết
• Định Luật 4: Định Luật Tác Dụng Và Phản Tác Dụng
• Hệ Lực Cân Bằng Khi Véc Tơ Chính Và Mô Men Chính Triệt Tiêu
• Định Luật 2 (Định Luật Cơ Bản Của Động Lực Học)
• Các Đặc Trưng Hình Học Của Cơ Hệ Và Vật Rắn
• Biểu Thức Của Mômen Động Lượng Của Vật Rắn Quay

Xem toàn bộ 180 trang tài liệu này.

d ≤ k

* Điều kiện cân bằng của vật rắn có kể đến ma sát lăn

- Hệ lực tác dụng lên vật rắn phải thoả mãn điều kiện cân bằng:

F1, F2,..., Fn, Fms , Ml 0

- Lực ma sát phải thoả mãn điều kiện giới hạn của nó: Fms ≤ fN

- Ngẫu lực ma sát lăn phải thoả mãn điều kiện giới hạn của nó: Ml ≤ kN

Ví dụ 2.4

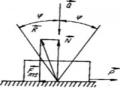
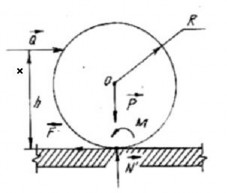
Trên đường nằm ngang có con lăn đồng chất bán kính R, trọng lượng P chịu lực đẩy Q theo phương ngang và cách mặt đường một đoạn h. Biết hệ số ma sát trượt f hệ số ma sát lăn k. Tìm giá trị của lực Q để con lăn cân bằng. (Hình 2.41)

Bài giải

Khảo sát con lăn cân bằng, tức không trượt và không lăn.

Hệ lực tác dụng lên con lăn có chiều như hình vẽ. Ta có hệ lực cân bằng: (Q, P, N, F, M )  0 Phương trình cân bằng

Q F  0

N P  0

M Q.h  0

Hình 2.41

F fN ; M kN

Từ các phương trình cân bằng ta nhận được: F = Q; N = P; M = Qh

Vậy: Điều kiện để con lăn không bị trượt sẽ là: Q ≤ f.P

Điều kiện để con lăn không bị lăn sẽ là: Q ≤ k .P

h

Thông thường k f

h

nên điều kiện không lăn thường bị vi phạm trước, nghĩa

là thông thường con lăn lăn trước khi trượt. Tuy nhiên với h quá bé có thể xảy ra trượt trước khi lăn.

2.2.2. Hệ lực không gian

2.2.2.1. Véctơ chính và mômen chính của hệ lực

1. Véc tơ chính của hệ lực

Định nghĩa: Véc tơ chính của hệ lực, ký hiệu tơ biểu diễn các lực của hệ lực.

R' , là tổng hình học của các véc

n 

R' F1 F2  ... Fn Fk

k 1

Phương pháp xác định véc tơ chính

(2.34)

a. Phương pháp vẽ đa giác lực: Để xác định véc tơ chính có thể vẽ đa giác lực. Muốn vậy, từ một điểm bất kỳ ta vẽ nối tiếp những véc tơ song song cùng chiều và có trị số bằng các véc tơ biểu diễn các lực của hệ lực. Đường gãy khúc nhận được gọi là

đa giác lực. Véc tơ OD được gọi là véc tơ khép kín đa giác lực. Vậy: Véc tơ chính của hệ lực chính là véc tơ khép kín của đa giác lực.

D

F2

F1

B

C

R

O

F3

A

F4

Hình 2.42

Trong trường hợp hệ lực phẳng, đa giác lực là đa giác phẳng, còn trong trường hợp hệ lực không gian, nói chung là đa giác ghềnh.

b. Phương pháp chiếu

Dựa vào công thức (2.34), véc tơ chính có thể được xác định qua các hình chiếu của nó theo các hình chiếu của các lực của hệ lực trên các trục toạ độ vuông góc Oxyz.

R' F F

 ... F F

n

x 1x 2 x







'

nx kx

k 1

n

R' Ry F1y F2 y  ... Fny Fky

(2.35)





R'

z

F1z

F2 z

 ... Fnz

k 1

n

Fkz

k 1

Từ đó mô đun và phương chiếu của véc tơ chính được xác định theo công thức:

R R 

'

2

'

2

x

y

R

'

z

2

R' (2.36)

R

'

cosx ; cos

R'

R' '

R

y ; cosz

R' R'

(2.37)

Trong đó: , ,là góc hợp bởi véc tơ chính với các trục toạ độ.

2. Mômen chính của hệ lực

Định nghĩa: Mômen chính của hệ lực đối với tâm O, ký hiệu là

M O là một véc

tơ bằng tổng hình học các véc tơ mômen của các lực thuộc hệ lực đối với tâm O.

n n

M Omo(F ) r F

(2.38)

k 1

k k k

k 1

Phương pháp xác định

a. Phương pháp vẽ: dựa vào công thức (2.38) ta thấy véc tơ mômen chính của hệ lực đối với và tâm O là véc tơ khép kín đa giác véc tơ, có các cạnh là các véc tơ song song cùng chiều và có trị số bằng các véc tơ mômen của các lực đối với điểm O. Đa giác véc tơ đó được gọi là đa giác véc tơ mômen được xây dựng tương tự đa giác lực, ở đó các lực được thay thế bằng mômen của nó đối với tâm O.

Vậy: Mômen chính của hệ lực đối với một tâm bằng véc tơ khép kín đa giác véc tơ mômen.

b. Phương pháp chiếu

0

F

O A

F

Hình

Chiếu phương trình (2.38) lên 3 trục toạ độ của hệ toạ độ vuông góc Oxyz và áp dụng định lý liên hệ giữa mômen của lực đối với một điểm và mômen của lực đối với một trục, ta có:

Ox

M

n n



mOx (Fk ) mx (Fk )

m m

F 

k 1

k 1 F

O Oy

M M

n n



mOy (Fk ) my (Fk )

(2.39)

k 1

k 1



M Oz

n n



mOz (Fk ) mz (Fk )

k 1

k 1

2.2.2.2. Thu gọn hệ lực về một tâm

1. Định lý dời lực song song

Định lý: Lực F đặt tại A tương đương với lực

2.43

F ' song song cùng chiều, cùng

cường độ với lực F nhưng đặt tại O và một ngẫu lực có mômen bằng mômen của lực

F đối với điểm O.

lực

Chứng minh: Áp dụng tiên đề 2, đặt tại O hai lực cân bằng ( F ' ,

F ' cùng phương chiều và cường độ với lực F . Ta có:

F  (F, F ', F ") F ' và (F, F ")

F '' ), trong đó

Lực

F ' chính là lực F dời song song đến O, còn hệ gồm hai lực (F, F")

là ngẫu

lực, có véc tơ mômen m mo (F ) . Đó là điều cần chứng minh.

Nhận xét: véc tơ mômen ngẫu lực

m mo F 

vuông góc với lực F , tức lực F

nằm trong mặt phẳng tác dụng của ngẫu lực. Vậy hệ lực gồm một lực F và ngẫu lực có véc tơ mômen m vuông góc với F (nghĩa là ngẫu lực và lực cùng nằm trong một

mặt phẳng) sẽ tương đương với một lực, tức có hợp lực

2. Thu gọn hệ lực về một tâm

R F vµ m0 Rm

Giả sử có một hệ lực bất kỳ ( F1 , F2 ,..., Fn ). Để thu gọn hệ lực này về tâm O ta lần lượt thu gọn từng lực về tâm O nhờ áp dụng định lý dời lực song song.

Cụ thể, (Hình 2.44)



F1F1vµ ngÉu lùc

M1 mo F1 

F

Fvµ ngÉu lùc M

m F 

2 2

2 o 2

...



F

Fvµ ngÉu lùc M

m F 

n n n o n

Vậy hệ lực đã cho ( F1 , F2 ,..., Fn ) tương đương với hệ lực đồng quy tại O

( F ' , F ' ,..., F ' ) và hệ ngẫu lực ( M1 , Mn ,..., Mn )

1 2 n

M

R

O

F

M1 

F1

F

2

Fn

O

1 F 

2

F

M 2 

n 

O

M n

Hình 2.44

Như đã biết hệ lực đồng quy có hợp lực qua O, được biểu diễn bằng véc tơ chính của hệ lực đặt tại O.

Gọi

' là hợp lực của hệ lực đồng quy, ta có:

R

O

n n

O k k

R'F ' F

R'

k 1 k 1

Hệ ngẫu lực ( M1 , Mn ,..., Mn ), tương đương với một ngẫu lực, có véc tơ mômen M :

n

M M M  ... M m (F )  ... m

(F ) m

(F ) M O

1 2 n O 1

O n O k k 1

Tâm O gọi là tâm thu gọn. Ta có định lý sau:

Định lý: Hệ lực không gian bất kỳ tương đương với một lực và một ngẫu lực đặt tại một điểm tùy ý, chúng được gọi là lực và ngẫu lực thu gọn. Lực thu gọn được biểu diễn bằng véc tơ chính của hệ lực đặt tại tâm thu gọn, còn ngẫu lực thu gọn có véc tơ mômen bằng mômen chính của hệ lực đối với tâm thu gọn.

3. Các dạng tối giản của hệ lực

Dựa vào kết quả thu gọn hệ lực về một tâm, ta nhận được các dạng tối giản của hệ lực như sau:

a. R '  0, M O  0 , hệ lực đã cho cân bằng.

b. R '  0, M O  0 , hệ lực đã cho tương đương với một ngẫu lực (không phụ

thuộc vào tâm thu gọn).

lực.

c. R '  0, M O R '  0 , hệ lực đã cho tương đương với một lực, tức hệ lực có hợp

d. R '  0, M O R '  0 , hệ lực đã cho tương đương với một hệ xoắn.

Đó là 4 dạng tối giản của hệ lực không gian bất kỳ.

Trong trường hợp hệ lực không gian có hợp lực, ta có định lý sau:

Định lý Varinhông: Trong trường hợp hệ lực không gian có hợp lực thì mômen của hợp lực đối với một tâm bất kỳ bằng tổng mômen của các lực thành phần đối với tâm ấy.

n

mO(R) mO(Fk)

k 1

* Các dạng tối giản (dạng chuẩn) của hệ lực đặc biệt

n

- Hệ lực đồng quy tại O: vì M O m (F )  0 , nên M O R '  0

O k

k 1

Vậy hệ lực đồng quy hoặc cân bằng hoặc có hợp lực.

- Hệ ngẫu lực: Véc tơ chính của hệ ngẫu lực luôn luôn bằng không

n

R ' Fk  0

k 1

Nên hệ ngẫu lực hoặc cân bằng hoặc tương đương với một ngẫu lực.

n

- Hệ lực song song: Véc tơ chính của hệ lực song song

song song với các lực thành phần.

R ' Fk

k 1

có phương

Véc tơ mômen chính của hệ lực:

M O m (F )

vuông góc với phương của

véc tơ chính R ' .

Vậy: M O R '  0

O k

n

k 1

Do đó: Hệ lực song song có các dạng chuẩn là: cân bằng, ngẫu lực, hợp lực.

2.2.2.3. Điều kiện cân bằng và các phương trình cân bằng của hệ lực

1. Hệ lực không gian bất kỳ

a. Điều kiện cân bằng

Điều kiện cần và đủ để hệ lực không gian cân bằng là véc tơ chính và mômen chính của hệ lực đối với một điểm bất kỳ phải đồng thời triệt tiêu.

n

R ' Fk 0

(F , F

,..., F )  0 

k 1

(2.40)

n

1 2 n



M O m

(F )  0

O k

k 1

Chứng minh: Điều kiện cần được chứng minh nhờ dựa vào các dạng tối giản của hệ lực. Thực vậy, nếu điều kiện (2.40) không được thoả mãn thì hệ lực không gian hoặc tương đương với một ngẫu lực hoặc một hợp lực hoặc một hệ xoắn, tức là không thoả mãn tiên đề 1, vậy hệ lực đã cho không cân bằng.

Điều kiện đủ là hiển nhiên vì véc tơ chính của hệ lực bằng không, khi thu gọn hệ lực về một điểm bất kỳ ta được một ngẫu lực thu gọn bằng mômen chính của hệ lực đối với điểm O, tức bằng không. Vậy ngẫu lực thu gọn là hai lực cân bằng, theo tiên đề 1, hệ lực đã cho cân bằng.

b. Các phương trình cân bằng

Từ điều kiện (2.5) ta có: điều kiện cần và đủ để hệ lực không gian cân bằng là tổng các hình chiếu của các lực trên ba trục toạ độ vuông góc và tổng mômen của các lực đối với ba trục ấy đều triệt tiêu.

n n n

Fkx  0;

k 1

Fky  0;

k 1

Fkz  0;

k 1

(2.41)

n n n

mx(Fk)  0; my(Fk)  0; mz(Fk)  0;

k 1

k 1

k 1

Muốn chứng minh ta chỉ cần chứng minh đây là điều kiện cần và đủ để có điều kiện (2.40). Đó là điều rò ràng.

Các phương trình (2.41) được gọi là các phương trình cân bằng của hệ lực không gian.

2. Hệ lực không gian đồng quy

Điều kiện cần và đủ để hệ lực không gian đồng quy cân bằng là véc tơ chính của hệ lực triệt tiêu.

n

R ' Fk  0

k 1

n n n

hoặc:

Fkx  0;

k 1

Fky  0;

k 1

Fkz  0;

k 1

(2.42)

Trong đó: vuông góc nhau.

Fkx , Fky , Fkz

k=1,2,...,n

là hình chiếu của lực trên ba trục toạ độ

3. Hệ lực không gian song song

Điều kiện cần và đủ để hệ lực không gian song song cân bằng là tổng hình chiếu của các lực lên trên trục z song song với các lực thành phần và tổng mômen của các lực đối với hai trục vuông góc với nhau x, y (và vuông góc với trục z) triệt tiêu:

n n n

Fkz  0; mx(Fk)  0; my(Fk)  0;

(2.43)

k 1

Ví dụ 2.5

k 1

k 1

Một trục kéo AB có đường trục nằm ngang và được đỡ trên hai ổ trục (bản lề

trục) A và B. Hai nhánh đai của puli có đường kính D  0,6m

chịu các lực căng

T1  5kN; T2  2kN . Vật được kéo có trọng lực P  5kN

và tang tời có đường kính

d  0,3m . Trục tời chịu tác dụng của ngẫu lực có mômen cản bằng M.

Xác định ngẫu lực cản M cần thiết để trục cân bằng và các phản lực tại các gối trục A và B. Bỏ qua ma sát, các kích thước cho trên hình 2.6.

z

a

ZA

2a M A y

a

r XA

P

ZB R

T2

B

XB

Bài giải:

Vật khảo sát là trục kéo.

T1

Hình 2.45

Các thành phần phản lực liên kết tác dụng vào trục kéo có chiều như hình vẽ. Trục kéo cân bằng dưới tác dụng của hệ lực:

P, M ,T1,T2 , X A , Z A , X B , ZB O

Các phương trình cân bằng của hệ lực có dạng:

FxT1T2X AX B 0

Fz P ZA ZB 0

mxF aP  4aZB 0

m F T DT

DP dM  0

y 1 2

2 2 2

mzF  3aT1 3aT2 4aX B 0

Thay các giá trị bằng số vào hệ phương trình trên và giải ra ta nhận được:

X A 1, 75kN;

ZB  1, 25kN;

ZA  3, 75kN;

M  0,15kNm

X B 5, 25kN;

Nhận xét: XA và XB < 0; ZA, ZB, M > 0

Vậy thành phần XA và XB có chiều ngược với chiều như hình vẽ.

Ví dụ 2.6

Cánh cửa OABC hình chữ nhật đồng chất có trọng lượng P được giữ cân bằng ở vị trí nằm ngang nhờ gối cầu O, bản lề C và dây BD. Biết đường chéo OB nghiêng 600 với cạnh OA, dây BD nằm trong mặt phẳng thẳng đứng qua OB và nghiêng góc 450 với OB. Tìm các phản lực tại O, C và sức căng

của dây.

Bài giải

- Chọn hệ trục toạ độ như hình vẽ

- Vật khảo sát là cánh cửa hình chữ nhật OABC

- Các phản lực liên kết có chiều như hình

vẽ

- Cánh cửa cân bằng dưới tác dụng của

hệ lực: (P, XO ,YO , ZO , XC , ZC ,T )  0

Phương trình cân bằng của hệ lực không gian là:

Fx X O X C Tx  0

Fy YO Ty  0

Fz ZOP Tz ZC 0

Hình 2.46

3

m (F ) P a 3Z a 3 T a  0

x 2 C z

m (F ) P aT a  0

y 2 z

mz (F ) X c a

Tx

3  0

2

T cos 450 cos 600 T

4

Trong đó:

T T cos 450 sin 600 T 6

2

x

4

T T sin 450 T

x2