Hệ Lực Cân Bằng Khi Véc Tơ Chính Và Mô Men Chính Triệt Tiêu



F1F1vµ ngÉu lùc m1m1F1

F Fvµ ngÉu lùc m m F 

2 2

2 2 2

...



F

Fvµ ngÉu lùc m

Có thể bạn quan tâm!

• Thông Số Làm Việc Chủ Yếu Của Bộ Truyền Bánh Răng
• Lực Liên Kết - Lực Hoạt Động - Phản Lực Liên Kết
• Định Luật 4: Định Luật Tác Dụng Và Phản Tác Dụng
• Điều Kiện Cân Bằng Và Các Phương Trình Cân Bằng Của Hệ Lực
• Định Luật 2 (Định Luật Cơ Bản Của Động Lực Học)
• Các Đặc Trưng Hình Học Của Cơ Hệ Và Vật Rắn

Xem toàn bộ 180 trang tài liệu này.

m F 

n n n n n

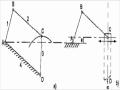
Như vậy thu gọn hệ lực F1, F2,..., Fn,

về tâm O ta được hệ lực đồng qui tại O :

F1, F2,..., Fn, và hệ ngẫu lực phẳng: m1, m2,..., mn

m

O

R

F1

O

F2

Fn

m1

m2

m3 O

F



1

F3

F2

R



Hình 2.33

Thu gọn hệ lực đồng qui tại O ta được véc tơ chính;

(2.17)

R0FkFkR

n

n

k 1 k 1

Thu gọn hệ ngẫu lực phẳng m1, m2,..., mn

ta được:

m m m  ... m m F m F  ... m F



12n 0 1 0 2 0 n

(2.18)

n

k

mm0

F m0

k 1

Vậy: Hệ lực phẳng bất kỳ tương đương với một lực và một ngẫu lực đặt tại một điểm tùy ý cùng nằm trong mặt phẳng tác dụng của hệ lực. Chúng được gọi là lực và ngẫu lực thu gọn. Lực thu gọn đặt tại tâm thu gọn có véc tơ lực bằng véc tơ chính của hệ lực còn ngẫu lực thu gọn có mô men bằng mô men chính của hệ lực đối với tâm thu gọn. Trong đó phương chiều và giá trị của lực thu gọn không phụ thuộc vào tâm thu gọn (vì véc tơ chính là véc tơ tự do) còn ngẫu lực thu gọn phụ thuộc vào tâm thu gọn.

2.2.1.3. Các dạng chuẩn của hệ lực phẳng

Dạng chuẩn là dạng đơn giản nhất nhận được khi thu gọn hệ lực. Từ kết quả thu gọn hệ lực phẳng về một tâm, ta nhận được các dạng sau:

1. Hệ lực cân bằng khi véc tơ chính và mô men chính triệt tiêu

R 0;

m0  0 F , F ,..., F  0

1 2

n

2. Hệ lực phẳng thu gọn về một ngẫu lực khi véc tơ chính triệt tiêu, còn mô men chính không triệt tiêu.

1 2

n

R 0;

m0  0 F , F ,..., F m0

Trong hai trường hợp trên vì

R 0

nên theo công thức (2.15), mô men chính

đối với mọi tâm đều bằng nhau và bằng

3. Hệ lực phẳng có hợp lực

m0 .

Khi

R 0, m0  0

thì F , F ,..., F Rtức là hệ đã cho có hợp lực đặt tại O có

1 2

n

0

véc tơ lực bằng véc tơ chính của hệ lực (hình 2.34a).

Khi

R 0, m0  0 , hệ lực thu gọn về tâm O được một lực R 

và một ngẫu lực

0

m0 , theo định lý dời lực song song có thể đưa về một lực có phương chiều và giá trị bằng phương chiều và giá trị của véc tơ chính nhưng đặt tại điểm O cách O một

m0

0

đoạn: h , Sao cho mô men của hợp lực R đối với điểm O bằng m (hình 2.34b)

R

tức là m

R

m F .

n

0 0 k

k 1

Từ đó ta có định lý sau:

Định lý Va Ri Nhông: Trong trường hợp hệ lực có hợp lực, mô men của hợp lực đối với một điểm bất kỳ bằng tổng đại số mô men của các lực của hệ đối với điểm đó:

n

m Rm F 

(2.19)

0 0 k

k 1

m0  0

O



R0

O

R

m0

O



R0

O

O

R0

h 

m0

R

a) Hình 2.34 b)

Như vậy hệ lực đồng qui có hai dạng chuẩn sau: Cân bằng nếu véc tơ chính của hệ lực triệt tiêu, hoặc có hợp lực nếu véc tơ chính của hệ lực không triệt tiêu.

Dạng chuẩn của một số hệ lực đặc biệt:

Hệ lực đồng qui: Cân bằng nếu mô men chính của hệ ngẫu lực triệt tiêu, hoặc ngẫu lực nếu mô men chính của hệ ngẫu lực không triệt tiêu.

Hệ lực phẳng song song cùng chiều chỉ có một dạng chuẩn là hợp lực vì véc tơ chính không triệt tiêu.

Hệ lực phẳng song song ngược chiều có thể có ba dạng chuẩn: Cân bằng, ngẫu

lực và hợp lực.

2.2.1.4. Điều kiện cân bằng và các phương trình cân bằng của hệ lực phẳng

1. Điều kiện cân bằng

Điều kiện cần và đủ để hệ lực phẳng cân bằng là véc tơ chính và mô men chính của hệ lực đối với một điểm bất kỳ phải đồng thời triệt tiêu.

R

n

Fk

F , F ,..., F  0 

k 1

(2.30)

n

1 2 n

0

m0 m

F 

k

Chứng minh:

k 1

Điều kiện cần: theo các dạng chuẩn của hệ lực nếu (2.30) không thỏa mãn thì hệ lực phẳng hoặc tương đương với một lực hoặc một ngẫu lực sẽ không thỏa mãn tiên đề 1.

Điều kiện đủ: khi véc tơ chính bằng không, hệ lực thu gọn về tâm O sẽ được một ngẫu lực thu gọn về hai lực. Nếu ngẫu lực bằng không thì hai lực đó là hai lực cân bằng.

2. Các dạng phương trình cân bằng của hệ lực phẳng

Điều kiện (2.30) có thể được viết dưới dạng các phương trình được gọi là các phương trình cân bằng.

* Dạng 1: Điều kiện cần và đủ để hệ lực phẳng cân bằng là tổng hình chiếu của các lực trên hai trục tọa độ vuông góc và tổng mô men các lực đối với một điểm O bất kỳ bằng không

n

n

F  0; F

 0; m F  0

(2.31)

n

kx ky

k 1 k 1

0 k

k 1

n

n

* Dạng 2: Điều kiện cần và đủ để hệ lực phẳng cân bằng là tổng mô men các lực đối với hai điểm A và B và tổng các hình chiếu của các lực lên trên trục không vuông góc với đoạn AB bằng không.

n

kx A k B k

F  0;

m F  0;

m F  0

(2.32)

k 1

k 1

k 1

* Dạng 3: Điều kiện cần và đủ để hệ lực phẳng cân bằng là tổng mô men của

n

n

các lực đối với ba điểm A, B, C không thẳng hàng triệt tiêu.

n

A k B k C k

m F  0;

m F  0;

m F  0

(2.33)

Ví dụ 2.1

k 1

k 1

k 1

Cột OA=2a, trọng lượng P thẳng đứng và chôn sâu xuống nền đất (ngàm) (hình 1.33). Cột chịu tác dụng lực nằm ngang F và đặt tại A và ngẫu lực m. Tìm: Phản lực tại ngàm.

Bài giải:

Khảo sát cân bằng của cột AB dưới tác dụng của hệ lực: trọng lực P , lực F và

ngẫu lực m , phản lực ngàm (gồm hai thành phần lực vuông góc

(hình 2.35). Vậy ta có:

X 0 ,Y0

và ngẫu lực

m0 )

0 0

X ,Y , m0, P, F , m 0

Viết phương trình cân bằng của hệ lực theo dạng 1:

A

F

m

2a

P

Y

0

m0

X0

O

Fx X 0 F  0

Fy

Y0

P  0

m0

F m0 m  2Fa  0

Khi giải hệ phương trình trên ta nhận được:

X F; Y P; m0 m  2aF

0 0

Trong các kết quả nhận được thì

Y0 và

m0 lấy

giá trị dương, nên chiều đã sử dụng như trên hình 2.35

là đúng, còn

X0 có giá trị âm nên chiều đã giả sử như

Hình 2.35

hình 2.35 là sai. Chiều đúng là chiều ngược lại.

2.2.1.5. Bài toán hệ lực phẳng với liên kết ma sát

Trong phần trước, khi xét liên kết tựa ta xem các vật tiếp xúc nhau tại một điểm và các mặt tựa tiếp xúc là hoàn toàn nhẵn. Khi đó phản lực liên kết nằm theo phương pháp tuyến của mặt tựa. Trên thực tế sự tiếp xúc xảy ra trẽn một diện tích nhỏ và các mặt tựa của các vật tiếp xúc vởi nhau là không nhẵn. Do đó, ngoài phản lực nằm theo phương pháp tuyến nói trên còn xuẩt hiện những lực và ngẫu lực cản được gọi là lực và ngẫu lực ma sát.

Xét hai vật rắn có liên kết tựa với nhau

Ma sát là hiện tượng xuất hiện những lực và ngẫu lực có tác dụng cản trở các chuyến động hoặc các xu hướng chuyển động tương đối của hai vật trên bề mặt cùa nhau.

Thường người ta phân làm ba loại ma sát.

- Ma sát tĩnh và ma sát động. Ma sát được gọi là tĩnh khi giữa hai vật mới chỉ có xu hướng chuyển động tương đối nhưng vẫn ở trạng thái cân bằng tương đổi và được gọi là động nếu chúng đă chuyển động tương đối với nhau.

- Ma sát trượt và ma sát lăn. Nếu xu hướng chuyển động hoặc chuyển động xảy ra giữa hai vật là trượt, ta có ma sát trượt, trường hợp xu hướng hoặc chuyển động xảy ra là lăn, ta có ma sát lăn.

- Ma sát khô và ma sát nhớt. Ma sát được gọi là khô khi hai vật tiếp xúc trực tiếp với nhau và được gọi là ma sát nhớt khi chúng tiếp xúc với nhau qua một màng dầu.

Ta xét một số Ví dụ sau

- Một khối hộp trên mặt nghiêng chịu ma sát trượt tĩnh khi khối hộp còn cân bằng và chịu ma sát trượt động khi đă xày ra chuyển động trượt.

- Môt bánh xe trên mặt nghiêng đổng thời chịu ma sát trượt tĩnh và ma sát lăn tĩnh khi bánh xe còn cân bằng và khi nó lăn không trượt thì có ma sát lăn động cùng với ma sát trượt tĩnh.

- Dây cu - roa truyền động giữa hai bánh xe chịu ma sát trượt tĩnh khi nó bám chặt và cùng chuyển động vối vành bánh xe và sẽ chịu ma

sát trượt động khi dây cu - roa bị trượt trên vành.

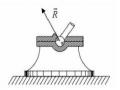
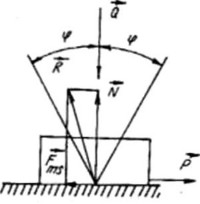
Bản chất vật lí của hiện tượng ma sát rất phức tạp. Lí thuyết thu gọn hệ lực có thế giúp chúng ta giải thích sự xuất hiện các lực và ngẫu lực ma sát. Do hai vật tiếp xúc với nhau không phải tại một điểm mà là trên một diện tích nào đó nên không phải xuất hiện một phản lực liên kết mà

là một hệ phản lực liên kết. Nếu xem đó là một hệ lực phẳng kết quả thu gọn cho một phản lực R và một ngẫu

Hình 2.36

lực M . Phân tích phản lực R ra hai thành phần pháp tuyến và tiếp tuyến chúng ta

được phản lực pháp N và lực ma sát là ngẫu lực ma sát lăn (Hình 2.36).

Fms

vuông góc với nhau. Còn ngẫu lực M chính

Dưới đây chúng ta khảo sát ma sát trượt và ma sát lăn chi trong trường hợp tĩnh và khô.

1. Bài toán cân bằng khi có ma sát trượt

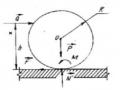
Để thiết lập định luật ma sát trượt chúng ta hãy quan sát hiện tượng xảy ra đổi với một vật rắn trên mặt nằm ngang, chịu lực ép (kể cả

trọng lực) Q thẳng góc với mặt bàn và chịu lực kéo P

theo mặt bàn (Hình 2.37). Ta thấy:

- Khi lực kéo P khá nhỏ thì vật rắn cân bằng.

- Tiếp tục tăng lực kéo P thì vật rắn vẫn cân bằng, nhưng khi lực kéo P tăng đến một giá trị P0 thì vật rắn bắt đầu trượt.

Điều đó có nghĩa là: vật rắn cân bằng khi trị số

của lực P không vượt quá giá trị P0: P ≤ P0

Từ thực nghiệm cho biết giá trị P0 tỷ lệ với lực ép Q và hệ số tỷ lệ f, nghĩa là:

P0 = f.Q

Hình 2.37

Hệ số tỷ lệ f phụ thuộc vào vật liệu tạo nên vật và mặt bàn và vào trạng thái bề mặt tiếp xúc (thô, ráp) giữa vật rắn và mặt bàn.

Từ đó suy ra:

- Ngoài phản lực pháp tuyến N cân bằng với lực ép còn có lực cân bằng với

lực kéo P gọi là lực ma sát, kí hiệu

Fms

Lực ma sát ngược chiều với lực kéo P nghĩa là ngược chiều với xu hướng trượt.

- Giá trị lực ma sát trượt không thế lớn tùy ý mà bị hạn chế, giá trị cực đại của nó tỉ lệ với giá trị của lực ép Q nghĩa là tỉ lệ với giá trị của phản lực pháp tuyến N .

Do đó, có thể phát biểu định luật ma sát trượt:

Lực ma sát trượt xuất hiện khi có xu hướng trượt tương đối, nằm theo tiếp tuyến của mặt tựa tiếp xúc, ngược hướng trượt và có giá trị bị chặn trên:

Fms ≤ fN

Trong đó: N là giá trị của phản lực pháp tuyến;

f- hệ số hằng số gọi là hệ số ma sát trượt tĩnh, khô. Nó có giá trị: Gỗ trên gỗ: f = 0,4  0,7

Kim loại trên kim loại: f = 0,15  0,25 Kim loại trên gỗ: f = 0,6

* Điều kiện cân bằng của vật rắn có kể đến ma sát trượt

- Hệ lực tác dụng lên vật rắn (bao gồm lực đã cho và lực liên kết trong đó có phản lực ma sát) phải thoả mãn điều kiện cân bằng: F1, F2,..., Fn, Fms  0

- Lực ma sát phải thoả mãn điều kiện giới hạn của nó: Fms ≤ fN

Ví dụ 2.2

Trên mặt OA có thể quay được quanh O ta đặt một vật nặng. Người ta nghiêng dần mặt OA, hỏi góc nghiêng  như thế nào thì vật bắt đầu trượt. Hệ số ma sát trượt giữa vật và mặt OA là f (Hình 2.38)

Bài giải:

Chọn hệ trục toạ độ như hình vẽ

Ta xét vật nặng. Vật chịu tác dụng của các lực có chiều như hình vẽ.

Khi vật ở trạng thái cân bằng, ta có:

(P, N , Fms )  0

Phương trình cân bằng:

x

y

N

Fms

P

Hình 2.38

Fms P sin 0 N P cos 0 Fms fN

Suy ra: tgFms 

fN f

(1)

(2)

(3)

(4)

N N

Vậy khi tgf vật rắn sẽ cân bằng, trạng thái cân bằng giới hạn khi tg = f

(5), quá đó vật sẽ trượt.

Nhìn vào phương trình (4) ta thấy thí nghiệm trên có thể dùng để xác định hệ số ma sát giữa vật và mặt OA.

f = tgtg = f

rút ra:  = 

Góc nghiêng giới hạn của mặt OA đúng bằng góc ma sát.

Ví dụ 2.3

Thang đồng chất AB có chiều dài 2l và trọng lượng P, tựa trên nền ngang Ox và tường thẳng đứng Oy đều không nhẵn và tường thẳng đứng Oy đều không nhẵn và có cùng hệ số ma sát trượt f. Tìm góc nghiêng  của thang với tường để thang cân bằng (Hình 2.39).

Bài giải

Chọn hệ trục toạ độ như hình vẽ

Khảo sát thang cân bằng ở trạng thái giới hạn (sắp sửa trượt). Thang chịu tác dụng của các lực như hình vẽ.

Ta thấy rằng nếu góc  càng lớn thì thang càng dễ bị trượt. Do đó góc  ứng với trạng thái giới hạn của thang sẽ có giá trị cực đại.

Ta có hệ lực cân bằng:

(P, NA , NB , FA , FB )  0

Hệ phương trình cân bằng:

Fx NB FA  0

Fy N A FB P  0

mo (F )  2N Al sin 2NBl cosPl sin  0

Hình 2.39

FA 

FB 

f .N A

f .NB

Từ các phương trình trên ta được:

N A 

P ;

1f 2

NB f

P ;

1f 2

tg

2 f

1f 2

Khi chú ý đến góc ma sát  (tg = f), ta có:

tg 2tgtg 21tg 2

Vậy:  = 2

Vì góc  tìm được ứng với trạng thái cân bằng giới hạn của thang, nên đó là giá

trị cực đại của góc .

Vậy điều kiện cân bằng của thang sẽ là:  ≤ 2

2. Bài toán cân bằng khi có ma sát lăn

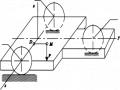
Để thiết lập định luật ma sát lăn ta hãy quan sát hiện tượng xảy ra đối với bánh xe có bán kính R đặt trên mặt nằm ngang, chịu lực nén thẳng đứng Q và chịu lực kéo nằm ngang P cùng đặt tại tâm O bánh xe (Hình 2.40a)

Hình 2.40

Theo quy tắc dời lực song song, có thể thay lực P bằng lực

P ' song song cùng

chiều và cùng trị số với lực P nhưng đạt tại tiếp điểm I và ngẫu lực cùng chiều quay

P quanh I và có mômen M = PR. Lực P ' gây trượt và ngẫu lực M gây lăn.

Để bánh xe không bị trượt P ' có giá trị không vượt quá giá trị cực đại có thể

đạt được của lực ma sát trượt, nghĩa là:

P ≤ f.N = f.Q

Hiện tượng lăn không xuất hiện nếu: M < M0

Từ thực nghiệm người ta thấy giá trị M0 tỷ lệ với giá trị của lực nén Q , tức tỷ lệ với giá trị của phản lực pháp tuyến N với hệ số tỷ lệ k, tức là:

M0 = k.N

Hệ số k được gọi là hệ số ma sát lăn, có thứ nguyên độ dài

Hệ số ma sát lăn phụ thuộc vào vật liệu tạo thành của hai vật tiếp xúc và trạng thái bề mặt tiếp xúc… thường hệ số ma sát lăn bé hơn nhiều lần hệ số ma sát trượt.

+ Gỗ trên gỗ: k = 0,05 ÷ 0,08

+ Thép trên thép: k = 0,005

+ Thép tôi trên thép tôi: k = 0,001

Định luật ma sát lăn.

Ngẫu lực ma sát lăn xuất hiện khi có xu hướng lăn tương đối, có chiều ngược với chiều xu hướng lăn và có giá trị:

Ml ≤ k.N

Vì hệ số ma sát lăn bé hơn nhiều lần so với hệ số ma sát trượt nên trong nhiều trường hợp ma sát lăn được bỏ qua.