Định Luật 4: Định Luật Tác Dụng Và Phản Tác Dụng

R

F1

0

F2

Hệ hai lực cùng đặt tại một điểm tương đương với một lực đặt tại điểm đặt chung, có véc tơ lực bằng véc tơ chéo hình bình hành mà hai cạnh là hai véc tơ biểu diễn hai lực thành phần (hình 2.10).

Định luật 3 cho phép xác định hợp lực của hai lực đồng qui và phân tích một lực thành hai lực thành phần theo qui tắc hình bình hành lực.

2.1.2.4. Định luật 4: Định luật tác dụng và phản tác dụng

Lực tác dụng và phản lực tác dụng giữa hai vật có cùng đường tác dụng, hướng ngược chiều nhau và có cùng cường độ (hình 2.11).

Hình 2.10

Định luật 4 là cơ sở để mở rộng các kết quả khảo sát đối với một vật sang khảo sát hệ vật.

F

A

B

FF

A B

F

Hình 2.12

2.1.2.5. Định luật 5: Định luật hóa rắn

Một vật biến dạng đang cân bằng dưới tác dụng của một hệ lực thì khi hóa rắn nó vẫn cân bằng.

Định luật 5 có thể hiểu là: một hệ lực đã có khả năng làm cho vật biến dạng cân bằngthì tất nhiên cũng có khả năng làm cho vật rắn cân bằng (ngược lại không dứt khoát đúng), và như thế khi có vật biến dạng cân bằng (dưới tác dụng của một hệ lực nào đó) ta có thể xem đó là vật rắn (hay thay bằng vật rắn) mà không có gì ảnh hưởng về mặt khảo sát lực.

Nhờ định luật 5 có thể sử dụng các kết quả đã nghiên

cứu cho vật rắn cân bằng cho trường hợp vật biến dạng cân bằng. Tuy nhiên, các kết quả đó chưa đủ để giải quyết bài

toán cân bằng của vật biến

Vật biến dạng cân bằng Vật rắn cân bằng

Vật rắn cân bằng Vật biến dạng cân bằng

dạng mà cần phải thêm các giả thiết về biến dạng (ví dụ định luật Húc trong sức bền vật liệu).

2.1.2.6. Định luật 6: Định luật giải phóng liên kết

Hình 2.13

trở nên không cân bằng

Vật không tự do (tức vật chịu liên kết) cân bằng có thể được xem là vật tự do cân bằng nếu ta, thay thế tác dụng của các liên kết bằng các phản lực liên kết tương

F1

F2

N1

N

2

F3

F

F2

1

N1

N2

F3

Hình 2.14

ứng (hình 2.14).

Nhờ định luật giải phóng liên kết, các định luật phát biểu cho vật rắn tự do vẫn đúng với vật rắn chịu liên kết, khi xem nó là vật tự do chịu tác dụng của hệ lực gồm các lực hoạt động tác dụng lên nó và các phản lực liên kết tương ứng với các liên kết được giải phóng.

Dưới đây sẽ trình bày một số quy tắc để tìm các đặc trưng của phản lực liên kết của một số liên kết thường gặp. Ta chỉ giới hạn đối với các liên kết không ma sát.

* Quy tắc xác định phản lực liên kết

- Phản lực liên kết nằm ngược với hướng mà theo đó chuyển động của vật bị cản trở.

- Nếu theo 1 phương nào đó mà chuyển động của vật không bị cản trở (phương tiếp tuyến) thì phản lực liên kết vuông góc với phương đó (hình 2.15a).

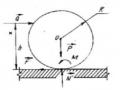
a. Liên kết tựa: Hai vật tựa trực tiếp lên nhau, chỗ tiếp xúc là bề mặt hoặc đường hoặc điểm. Phản lực tựa có phương vuông góc với mặt tựa (hoặc đường tựa)

(hình 2.15). Ký hiệu là N .

NB

B

	N

Có thể bạn quan tâm!

• Các Định Lý Hợp Vận Tốc, Hợp Gia Tốc
• Thông Số Làm Việc Chủ Yếu Của Bộ Truyền Bánh Răng
• Lực Liên Kết - Lực Hoạt Động - Phản Lực Liên Kết
• Hệ Lực Cân Bằng Khi Véc Tơ Chính Và Mô Men Chính Triệt Tiêu
• Điều Kiện Cân Bằng Và Các Phương Trình Cân Bằng Của Hệ Lực
• Định Luật 2 (Định Luật Cơ Bản Của Động Lực Học)

Xem toàn bộ 180 trang tài liệu này.

N

		NA
a)	b) Hình 2.15	A c)

t

A

t

B

- Vật tựa lên mặt (Hình 2.15a).

- Giá tựa trên con lăn (Hình 2.15b).

- Vật tựa lên điểm nhọn. Phản lực có

A

T1

T2

B C

P

hướng pháp tuyến với bề mặt của vật (Hình

2.15c).

b. Liên kết dây mềm, thẳng và không giãn: phản lực của dây tác dụng lên vật khảo sát

T

P

Hình 2.16

Hình 2.17

đặt vào điểm buộc dây và hướng vào dây. Phản lực của vật rắn tác dụng lên dây gọi là sức căng dây, ký hiệu là T . Sức căng dây hướng dọc dây và

hướng ra đối với mặt cắt dây (hình 2.16).

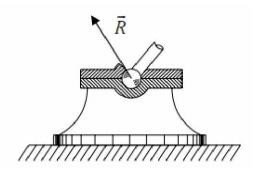
c. Liên kết bản lề: Hai vật có liên kết bản lề khi chúng có trục (chốt) chung. Trong trường hợp này hai vật tựa vào nhau nhưng điểm tựa chưa xác định. Phản lực liên kết R đi qua tâm của trục và có phương chiều chưa xác định. Phản lực được phân thành hai

thành phần vuông góc với nhau YAX A, nằm trong

mặt phẳng vuông góc với đường trục của tâm bản lề (hình 2.17).

YA

A

X

A

NB

B

d. Liên kết gối: Để đỡ các dầm và khung... người ta dùng các liên kết, có dạng gối cố định (hình 2.18a) và gối con lăn (hình 2.18b). Phản lực liên kết của gối cố định

được xác định như liên kết bản lề, còn phản lực liên kết của gối con lăn được tìm theo quy tắc của phản lực liên kết tựa.

a) b)

Hình 2.18

z

Rz

R

Rx

x

Ry

y

Hình 2.19a

Hình 2.19b

e. Liên kết gối cầu: Được thực hiện nhờ một quả cầu gắn vào đầu của vật chịu liên kết và được đặt vào trong một vỏ cầu gắn liền với vật gây liên kết. Phản lực gối cầu đi qua tâm O của vỏ cầu, có phương, chiều chưa xác định. Thường phản lực gối

cầu phân thành ba thành phần vuông góc Rx, Ry, Rz(hình 2.19a-b).

Hình 2.20

Hình 2.21

60

f. Liên kết ngàm: Là liên kết khi vật được nối cứng vào một vật khác (Ví dụ như hàn). Trong trường hợp ngàm phẳng phản lực liên kết gồm hai lực thẳng góc với nhau và một ngẫu lực nằm trong mặt phẳng chứa hai lực (hình 2.20). Đối với ngàm không gian, phản lực liên kết gồm ba thành phần lực vuông góc với nhau (dọc theo ba trục tọa độ) và ba thành phần ngẫu lực trong ba mặt phẳng tọa độ (hình 2.21).

g. Liên kết thanh

Liên kết thanh được thực hiện nhờ các

thanh thỏa mãn điều kiện sau: Chỉ có lực tác dụng ở hai đầu, còn dọc thanh không có lực tác dụng và

trọng lượng thanh được bỏ qua. Phản lực S có phương qua điểm đầu và điểm cuối của thanh (hình 2.22). A

Phản lực S gọi là ứng lực của thanh là lực

do thanh tác dụng vật khảo sát.

2.1.3. Các hệ quả

SA SB

B

Hình 2.22

Từ các định luật đã nêu trên ta nhận được các A

kết quả sau: F1 B

O

2.1.3.1. Hợp các lực đồng qui F2

Giả sử hệ lực đặt tại O (trường hợp hệ lực có

đường tác dụng đi qua O thì áp dụng hệ quả trượt lực có thể đưa về trường hợp này). Áp dụng trực tiếp tiên

đề 3 ta tìm được hợp lực R của hệ lực (hình 2.23).

Hợp lực đi qua điểm đồng qui O và có véc tơ

R

F

3 C

Hình 2.23

lực.

R F1 F2  ... Fn Fk

n

k 1

(2.5)

Để xác định véc tơ lực của hợp lực có thể sử dụng phương pháp vẽ hoặc phương pháp xác định hình chiếu của nó trên ba trục vuông góc.

1. Phương pháp vẽ

Hợp lực được biểu diễn bằng véc tơ khép kín của

đa giác lực được xây dựng như sau: Từ đầu mút của véc A’

tơ biểu diễn lực F1

vẽ véc tơ AB song song và bằng véc B’ O’

tơ lực

F2 , từ B vẽ véc tơ BC song song và bằng véc tơ R

lực F3

và cứ thế tiếp tục cho đến lực cuối cùng

Fn n  3. Đa giác lực OABC là đa giác lực của hệ 3 lực

Hình 2.24 C’

F1, F2, F3

F1, F2, F3.

cạnh OC là véc tơ khép kín đa giác lực, nó biểu diễn hợp lực của hệ ba lực

Vì hợp lực phải đi qua điểm O , nên đa giác lực không cần thiết phải vẽ xuất

phát từ điểm đồng qui mà có thể từ một điểm O

tùy ý (Hình 2.24). Véc tơ khép kín

Rcủa đa giác lực xuất phát từ một điểm O

bất kỳ được gọi là véc tơ chính của hệ

lực, ký hiệu là

R.

RFk

n

k 1

(2.6)

Từ đó ta có định lí sau: Hợp của hệ lực đồng qui được biểu diễn bằng véc tơ chính của hệ lực đặt tại điểm đồng qui.

2. Phương pháp hình chiếu

z

Rz

Rxz

R

Ry

y

Rx

Rxy

x

Hình 2.25

O

Khi chiếu hai vế của đẳng thức véc tơ (2.5) lên 3 trục tọa độ vuông góc ta được (hình 2.25):

n

Rx F1x F2 x  ... Fnx Fkx

k 1

n

Ry F1y F2 y  ... Fny Fky

(2.7) () (

k 1

n

RzF1z F2 z  ... Fnz Fkz

k 1

Đó là 3 hình chiếu của véc tơ hợp lực lên 3 trục tọa độ vuông góc. Từ đó có thể xác định được giá trị phương chiều của hợp lực:

R2 R2 R2

x y z

R 

R R R

cos 0x, RRx ; cos 0 y, R Ry ; cos 0z, R Rz

2.1.3.2. Các định lí biến đổi tương đương ngẫu lực

(2.8)

Định lí 1.1: Hai ngẫu lực cùng nằm trong một mặt phẳng, có cùng chiều quay và cùng trị số mô men thì tương đương nhau (hình 2.26).

Định lí 1.2: Tác dụng của ngẫu lực không thay đổi khi nó dời đến những mặt phẳng song song (hình 2.25).

Định lí 1.3: Hai ngẫu lực có véc tơ mô men bằng nhau thì tương đương nhau (hình 2.28).

Như vậy, tác dụng của ngẫu lực hoàn toàn được đặc trưng bằng véc tơ mô men ngẫu lực m .

Trong trường hợp riêng khi xét tác dụng của ngẫu lực trong mặt phẳng thì tác

dụng của nó hoàn toàn được đặc trưng bằng mô men đại số ngẫu lực m F.d

m1 Fd

P

m2 Fd

P

F

F

F

F

Hình 2.26 Hình 2.27

m

Fd

P

m

Fd

P

Hình 2.28

Định lí 1.4: Hợp các ngẫu lực được một ngẫu lực, có véc tơ bằng tổng các véc tơ mô men các ngẫu lực đã cho (hình 2.29).

m mk

n

k 1

(2.9)

Định lí 1.5: Hợp các ngẫu lực trong cùng một mặt phẳng được một ngẫu lực nằm trong mặt phẳng đã cho, có mô men đại số bằng tổng mô men đại số các ngẫu lực đã cho.



n

m mk

k 1

(2.10)

m

m

1

m

m

2

1

m2

m

m

Hình 2.29

2.2. KHẢO SÁT HỆ LỰC

2.2.1. Hệ lực phẳng

Hệ lực phẳng bất kỳ là một tập hợp các lực tác dụng lên cùng một vật rắn và có đường tác dụng cùng nằm bất kỳ trong một mặt phẳng (hình 2.30).

2.2.1.1. Véc tơ chính và mô men chính của hệ lực phẳng

1. Véc tơ chính của hệ lực phẳng

Định nghĩa: Cho hệ lực phẳng F1, F2,..., Fn, véc tơ chính của hệ lực, ký hiệu là Rlà véc tơ tổng của các véc tơ lực của hệ lực:

RF1 F2  ... Fn

Phương pháp xác định véc tơ chính:

F1

F

2

F3

Hình 2.30

(2.11)

Sử dụng phương pháp vẽ đa giác lực. Trong trường hợp này đa giác lực là đa giác phẳng (Hình 2.31).

D

F2

F1

B

C

R

O

F3

A

F4

Hình 2.31

Dùng phương pháp hình chiếu của lực trên các trục tọa độ vuông góc. Trong trường hợp này chỉ cần xác định hai hình chiếu của nó trên hai trục vuông góc với nhau.

RF F

 ... F

F

x



1x 2 x nx kx k 1

n

(2.12)

n

RF F

 ... F

F

y

1y 2 y ny ky k 1

giá trị và phương chiều của véc tơ chính được xác định theo công thức.

RR2R2; cos ox, RRx ; cos oy, RRy

(2.13)

x y RR

2. Mômen chính của hệ lực phẳng

Mô men chính của hệ đối với điểm O: là đại lượng đại số, ký hiệu là m0 bằng

tổng mô men của các lực của hệ đối với điểm O :

m0 m

F m

F  ... m

F 

m F 

(2.14)

Nhận xét:

0 1 0 2 0 n

0 k

n

k 1

Véc tơ chính là véc tơ tự do, còn mô men chính phụ thuộc vào điểm lấy mô men, nghĩa là mô men chính lấy với hai điểm khác nhau sẽ khác nhau:

0 0

m0m0 mR 

(2.15)

Trong đó

movà m0

là mô men chính của hệ đối với điểm O' và O tương ứng

còn

m0R0là mô men đối với điểm Ocủa véc tơ chính đặt tại điểm O .

Đối với hệ lực đồng qui thì mô men chính của hệ lực đối với điểm đồng qui

bằng không. Đối với hệ ngẫu lực thì véc tơ của hệ ngẫu lực luôn luôn bằng không, còn mô men chính của hệ ngẫu lực đối với điểm bất kỳ O nào cũng bằng mô men của ngẫu lực tổng cộng tức bằng mô men của các ngẫu lực thành phần của hệ ngẫu lực.

2.2.1.2. Thu gọn hệ lực phẳng

1. Định lý dời lực song song

Lực F đặt tại A tương đương với lực F ' bằng nó nhưng đặt tại O và một ngẫu

lực có mô men bằng mô men của lực F đối với điểm O (hình 2.32).

F F vµ m m0 F 

(2.16)

O

m m0F 

F

A

F

O

A

F

F

O

F

Chứng minh định lý này giống như chứng minh cho trường hợp hệ lực không gian khi thay thế véc tơ mô men bằng mô men đại số.



Hình 2.32

2. Thu gọn hệ lực về một tâm

Giả sử có một hệ lực phẳng bất kỳ ( F1 , F2 ,..., Fn ): Yêu cầu thu gọn hệ lực đó. Lấy một điểm O trong mặt phẳng tác dụng của hệ lực gọi là tâm thu gọn. Sử dụng định lý dời lực song song để dời các lực về tâm O (hình 2.33).

Xem tất cả 180 trang.