Sự Thay Đổi Kích Thước Bước Dựa Trên Giá Trị Tuyệt Đối Của Gradient

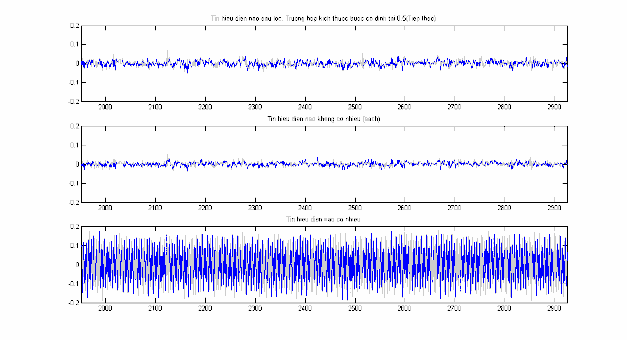
Hình 2.20: EEG trước và sau lọc nhiễu, đoạn n  2001  3000 .

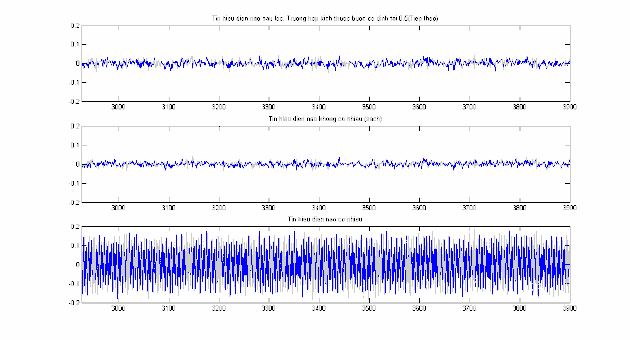
Hình 2.21: EEG trước và sau lọc nhiễu, đoạn n  3001  4000 .

So sánh tín hiệu điện não sau lọc (trên cùng) với tín hiệu điện não sạch

(giữa) trong pha tiếp theo trên hình 2.19 cho thấy tín hiệu sau lọc đạt đến tín hiệu điện não sạch nhiễu S n .

(n)

chưa

Điều này cũng được phản ánh qua sai số trung bình bình phương tại

hình 2.12 và hình 2.13. Độ nhấp nhô của MSE tăng lên khi kích thước bước

thích nghi tăng từ   0.05 đến   0.5 .

2.3. Thuật toán LMS với kích thước bước thay đổi

Các kết quả thực nghiệm trình bày ở mục trên cho thấy một phân lớp sơ bộ đối với kích thước bước trong sử dụng thuật toán LMS và gợi ý về các mô hình “trộn” (xem [29]), sử dụng các lớp khác nhau của kích thước bước để khai thác tốt ưu điểm của từng lớp. Tuy nhiên đề xuất trong [29] mới giải quyết được trường hợp tín hiệu điện não với giả thiết mạnh về giá trị trọng số khởi tạo. Đây là kết quả quan trọng nhưng không áp dụng trực tiếp được cho trường hợp lọc nhiễu điện tim do bản chất khác nhau khá xa của hai lớp tín hiệu này. Phân bố về độ lớn của gradient đã cung cấp ý tưởng và là cơ sở cho đề xuất của luận án về cách thay đổi giá trị kích thước bước thích nghi để tạo ra mô hình “trộn” áp dụng cho nhiều lớp lọc nhiễu khác nhau trong lọc nhiễu tín hiệu của điện tâm đồ và điện não đồ. Phần này giới thiệu cơ sở toán học của phương pháp và các kết quả thực nghiệm trong việc sử dụng cách tính mới để cập nhật kích thước bước thích nghi để lọc nhiễu trong quá trình ghi tín hiệu điện tim và điện não. Các kết quả thực nghiệm minh hoạ và so sánh hiệu năng giữa thuật toán đề xuất với thuật toán LMS với kích thước bước thích nghi cố định.

2.3.1. Sự thay đổi kích thước bước dựa trên giá trị tuyệt đối của Gradient

Để tăng tốc độ hội tụ của thuật toán LMS, Daniel Olguín Olguín trong

[29] đề xuất việc thay đổi kích thước bước thích nghi theo công thức:

trong đó

 n  1  n  2n , (2.22)

 : Yếu tố quên, có giá trị nằm trong dải: 0    1, thường được

chọn   0.98

 : Tham số kích thước bước thích nghi của  , thường được chọn thoả

mãn điều kiện   0

Đề xuất trên xuất phát từ bài toán lọc nhiễu cho tín hiệu điện não đồ (EEG) với đóng góp chính thể hiện ở công thức (2.22), đó là phương pháp thay đổi kích thước bước thích nghi. Tuy nhiên (2.22) chỉ phù hợp đối với bài toán lọc nhiễu cho tín hiệu điện não đồ do đặc tính biến đổi đều của lớp tín hiệu này với giá trị biên của tín hiệu nằm trong khoảng

0.15  max

 0.15 (xem [5], [29]). Độ rộng khe triệt của bộ lọc triệt tần

phản ánh mức độ suy giảm đến các tín hiệu có tần số lân cận tần số triệt tại

0 (xem [44]). Độ rộng khe triệt được tính như sau:

BW

Trong đó:

BW : Độ rộng khe triệt.

 2C 2 ,

 : Kích thước bước thích nghi.

C : Biên độ của tín hiệu nhiễu tham chiếu (xem công thức 2.8 và 2.9).

Do vậy khi thuật toán hội tụ  có thể nhận giá trị đủ nhỏ để độ rộng khe triệt đủ hẹp. Trong tín hiệu điện tâm đồ (hình 1.1), đỉnh R tại mỗi chu kỳ

hoạt động có đặc tính biến đổi đột ngột. Do vậy phép tính 2n 

trong (2.22)

có thể dẫn đến việc không thoả mãn điều kiện ổn định của thuật toán và làm mất các thông tin hữu ích khi độ rộng khe triệt quá lớn. Hơn thế nữa tác giả trong [29] gán giá trị  lớn khi khởi tạo và sử dụng công thức (2.22) để làm

 giảm dần đến giá trị tốt nhất. Điều này có thể làm cho thuật toán không hội tụ hoặc hội tụ chậm nếu ngẫu nhiên ta chọn điểm khởi tạo của ma trận trọng số gần điểm cực tiểu.

Theo [3], [27], [30] nhiễu cũng bị biến đổi trong quá trình lan truyền từ nguồn nhiễu đến đầu thu tham chiếu. Sự sai lệch này được mô hình hoá bằng 1 đại lượng ngãu nhiên có phân phối Gaussian. Và được mô tả trong công

thức sau:

Nn x1n normrnd mean ,sigma . Độ lệch chuẩn

sigma phản ánh khoảng cách từ điểm cực tiểu đến điểm khởi tạo của ma trận trọng số. Mối quan hệ giữa độ lệch chuẩn với số vòng lặp được mô tả trong bảng 2.1 và trong hình (2.22) và (2.23).

Bảng 2.1: Mối quan hệ giữa độ lệch chuẩn và số vòng lặp cần thiết

cho thuật toán hội tụ.

TT

Độ lệch chuẩn	Số vòng lặp cần thiết để thuật toán hội tụ
	Thay đổi kích thước bước dùng công thức 2.20	Thay đổi kích thước bước dùng công thức 2.21
1	0.01	500	450
2	0.005	500	400
3	0.0001	520	370
4	0.00005	520	350
5	0.000001	530	300

Có thể bạn quan tâm!

• Cơ Sở Toán Học Của Phương Pháp Thích Nghi Dựa Trên Thuật Toán
• Phương Pháp Thích Nghi Lọc Nhiễu Điện Áp Cho Các Tín Hiệu Y Sinh
• Kết Quả Lọc Nhiễu Đối Với Tín Hiệu Điện Não
• Mse Trường Hợp   0.05 ,   0.5 Và  Thay Đổi.
•  Thay Đổi, Eeg Trước Và Sau Lọc Nhiễu, Đoạn N  2001  3000 .
• Kỹ Thuật Làm Nổi Bật Đặc Tính Của Nhiễu Bằng Biến Đổi Fourier.

Xem toàn bộ 130 trang tài liệu này.

Qua đó dễ dàng thấy rằng nếu không thoả mãn giả thiết ngặt nghèo về chọn giá trị trọng số khởi tạo, thuật toán sẽ hội tụ chậm. Không may là trong nhiều thực nghiệm giả thiết này không được thoả mãn. Đề xuất của luận án

dựa trên sự khai thác thông tin về sự thay đổi độ lớn của véc tơ gradient trong thuật toán LMS.

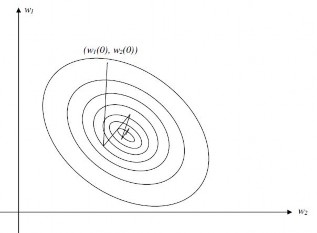
Hình 2.22: Sự hội tự của thuật toán LMS sử dụng công thức (2.22) cho điều

chỉnh  n , với điều kiện toạ độ w1 0,w2 0 được chọn phù hợp

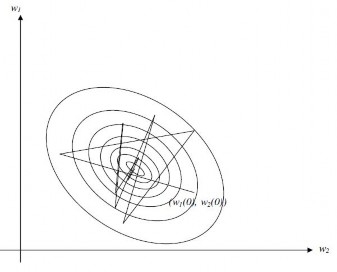
Hình 2.23: Sự hội tự của thuật toán LMS sử dụng công thức (2.22) cho điều

chỉnh  n , khi w1 0, w2 0 không phù hợp.

Đối với hàm bậc II xác định dương thì Gradient có giá trị lớn khi ở xa điểm cực tiểu, và có giá trị nhỏ khi ở gần điểm cực tiểu (Hình 2.24). Ý tưởng

của luận án có thể mô tả trên mặt phẳng w1, w2(xem [44]). Tại thời điểm k, kích thước bước thích nghi nên nhận giá trị lớn khi toạ độ

1 2

w1 n ,w2 n cách xa tọa độ w * , w* của điểm cực tiểu của bề mặt hiệu năng bậc II (xem [44]). Ngược lại kích thước bước thích nghi nên nhận giá trị

nhỏ khi

w1 n ,w2n gần toạ độ của điểm cực tiểu. Sự lựa chọn kích

thước bước thích nghi như vậy sẽ giúp thuật toán lọc thoả mãn các điều kiện về tốc độ hội tụ và độ ổn định của thuật toán. Chúng tôi nhận thấy rằng phân bố độ lớn của Gradient (  ) trên mặt phẳngw1,w2 có tính chất gần như đáp ứng được ý tưởng trên (xem [38]), và công thức cập nhật bước thích nghi được đề nghị như sau:

,

 n  1 

x1n  n 



max  x1



n  m m

 1,..., n  N 2

trong đó: N là số mẫu trong 1 chu kỳ của tín hiệu tham chiếu,

 : Độ rộng lý tưởng cho dải triệt (Xem [3] [29], [44])

(2.23)

max  x1n m 

m 1,..., n  N 2trả lại giá trị C 2

tại thời điểm n

n : Kích thước bước cho việc điều chỉnh trọng số tại thời điểm n .

Chú ý rằng, số hạng thứ nhất của vế phải của (2.23)

 x1(n)(n)

  1

2

(n)

phản ánh việc phân bố độ lớn của Gradient (  )

trên mặt phẳngw1,w2 ,

x1(n) : Nhiễu thu được ở đầu vào tham chiếu tại thời điểm n ,

(n) : Đầu ra của bộ lọc nhiễu tại thời điểm n ,

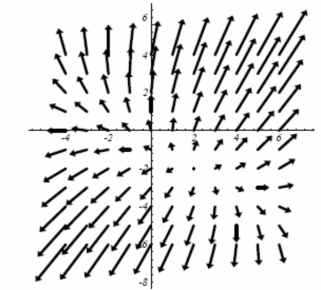
1 2

Hình 2.24: Gradient của  trên mặt phẳng (w , w ) .

Chúng tôi đã xác định điều kiện hội tụ của bộ lọc triệt tần sử dụng công thức (2.23) và được cho trong bổ đề sau:

Bổ đề. Với   1

2

các dãy (2.11) và (2.12) với  cho bởi (2.23) sẽ hội tụ.

Chứng minh.

Từ công thức (2.8), (2.11) và (2.23) ta có

2

(n)  S(n)  wi( n) xi( n) , (2.24)

i 1

và

w1n  1 w1n  2(n  1) n x1n ;



  2 

 1  2

 C

x (n) w n  F , (2.25)

2 1  1 n

trong đó Fn

bị chặn bởi hằng số M độc lập với n

Sự hội tụ của công thức trên được phản ánh qua kỳ vọng của v1n của hệ thống tuyến tính.

Xét hệ tuyến tính xấp xỉ v1(n)  cho bởi



  2 

v1n  1 1  2

 C

x (n)  v n . (2.26)

2 1  1

Kỳ vọng của

công thức

v1n  1được tính dựa trên (2.16) và được xác định bằng

  n2

  

1 

2   

E v (n  1)   1  2

l 1  C

E x1(l) E v0;





0 

1  nEv

(2.27)

Giả thiết   1

2

đảm bảo sự hội tụ của hệ thống tuyến tính. Chứng minh sự

hội tụ của kỳ vọng của dãy (2.11) với  cho bởi (2.23) dựa trên đánh giá (2.27) và ước lượng



k  2 2  k

E 1 

l 1 

x (l)  F

C 2 1  n k

 M (1  ) .

Chứng minh hội tụ đối với dãy w2nđược thực hiện tương tự.

2.3.2. Thực nghiệm và kết quả

Để đánh giá kết quả ta dùng công thức (2.7). Tốc độ hội tụ của thuật toán được phản ánh qua tốc độ hội tụ về giá trị 0 hoặc xấp xỉ 0 của MSE. Độ ổn định của thuật toán được phản ánh thông qua sự thay đổi của MSE sau khi thuật toán đã hội tụ.

2.3.2.1. Đối với tín hiệu điện tim

Trong hình vẽ 2.25 chúng tôi biểu diễn MSE trong ba trường hợp