 Thay Đổi, Eeg Trước Và Sau Lọc Nhiễu, Đoạn N  2001  3000 .

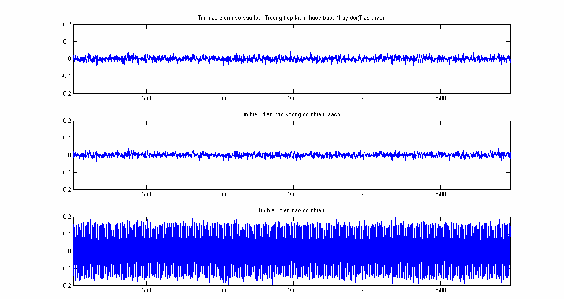
Hình 2.34:  thay đổi, EEG trước và sau lọc nhiễu, đoạn n  2001  3000 .

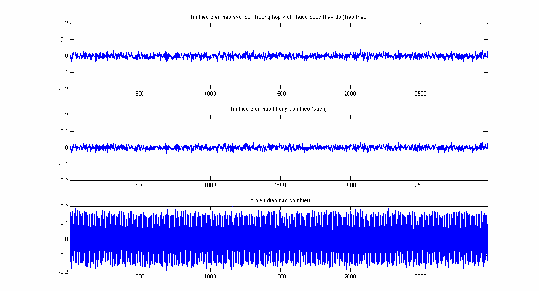
Hình 2.35:  thay đổi, EEG trước và sau lọc nhiễu, đoạn n  3001  4000 .

Kết quả của luận án có thể so sánh đựoc với các kết quả tiêu biểu trong các nghiên cứu gần đây về nâng cao hiệu năng của thuật toán LMS trong lĩnh vực xử lý tín hiệu điện não: sử dụng trường hợp kích thước bước thay đổi

trong [29] thuật toán hội tụ, MSE đạt đến

Có thể bạn quan tâm!

• Kết Quả Lọc Nhiễu Đối Với Tín Hiệu Điện Não
• Sự Thay Đổi Kích Thước Bước Dựa Trên Giá Trị Tuyệt Đối Của Gradient
• Mse Trường Hợp   0.05 ,   0.5 Và  Thay Đổi.
• Kỹ Thuật Làm Nổi Bật Đặc Tính Của Nhiễu Bằng Biến Đổi Fourier.
• So Sánh Kết Quả Phép Biến Đổi Sóng Nhỏ Dùng Các Thangs  21 Và
• Đánh Giá Độ Chính Xác Và Mức Độ Phức Tạp Tính Toán Của Giải Thuật Tìm Tần Số 0 Của Nhiễu.

Xem toàn bộ 130 trang tài liệu này.

5.106

sau xấp xỉ 400 vòng lặp,

trong khi đề xuất của chúng tôi cho phép thuật toán hội tụ sau 450 vòng lặp với độ ổn định tốt. Để minh hoạ cho việc so sánh, chúng tôi đã làm thực nghiệm lại phương pháp trong [29], kết quả thu được hoàn toàn giống như các kết quả trong [29]. Do vậy chúng tôi sẽ sử dụng các kết quả mô phỏng này để làm căn cứ so sánh 2 phương pháp trong hình 2.36.

Qua hình 2.36 ta thấy rằng: Nếu sử dụng công thức 2.23 để điều chỉnh kích thước bước thích nghi, thuật toán LMS sẽ hội tụ nhanh hơn và có độ ổn định tốt hơn.

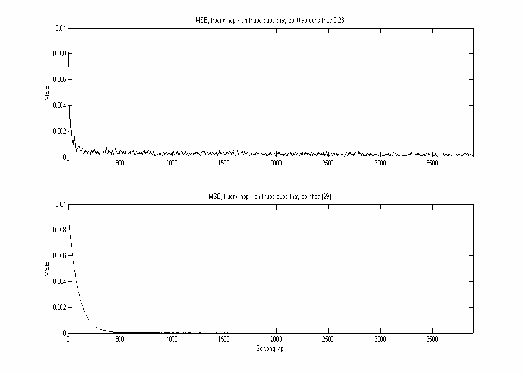
Hình 2.36: So sánh với phương pháp thay đổi kích thước bước trong [29].

KẾT LUẬN

Trong chương này chúng tôi đã xây dựng một số cơ sở toán học cần thiết cho các phương pháp thích nghi trong lọc nhiễu: xác định các điều kiện cần, đủ để các thuật toán hội tụ và xây dựng phần mềm nhúng thực hiện các thuật toán này. Các đánh giá về phương pháp của luận án được tiến hành thông qua việc so sánh với các phương pháp mới nhất của các tác giả khác về nâng cao hiệu năng của thuật toán LMS dựa trên kích thước bước thay đổi. Trong phạm vi luận án chúng tôi chỉ trình bày một số kết quả thực nghiệm tiêu biểu để minh hoạ những ưu việt của phương pháp thích nghi của chúng tôi trong việc cho phép thuật toán LMS tuy hội tụ chỉ nhanh hơn 50 vòng lặp so với phương pháp được nêu trong [29] đối với bài toán lọc nhiễu trong tín hiệu điện não nhưng độ ổn định thực nghiệm lại cao hơn. Không những thế phương pháp đề xuất bằng công thức 2.23 còn có thể được áp dụng cho bài toán lọc nhiễu trong tín hiệu điện tim trong khi thuật toán đề xuất trong [29] không đảm bảo để thuật toán hội tụ.

Chương 3

Một giải pháp điều chỉnh thích nghi bộ lọc triệt tần với tiếp cận sóng nhỏ.

Trong bài toán lọc nhiễu ra khỏi tín hiệu điện tim, nguồn gây nhiễu là đường tải điện, nhiễu có đặc điểm là chỉ tồn tại trên 1 tần số, do vậy giải pháp phù hợp là sử dụng bộ lọc triệt tần có tần số triệt trùng với tần số của nhiễu. Tuy nhiên, khi tần số của nhiễu thay đổi ngẫu nhiên xung quanh tần số của các tín hiệu cần bảo tồn thì bài toán lọc nhiễu có thể coi như bài toán điều chỉnh tần số triệt của bộ lọc triệt tần với dải triệt đủ hẹp sao cho chỉ loại bỏ nhiễu 1 tần số mà không làm suy giảm đến các tín hiệu có tần số lân cận. Bộ lọc triệt tần thích nghi được xem là một trong số giải pháp tốt nhất cho vấn đề này (xem [8], [12], [19], [29]). Đặc biệt, việc sử dụng thuật toán LMS với kích thước bước thay đổi đã đáp ứng được 2 yêu cầu trên, đồng thời cải thiện đáng kể hiệu năng của bộ lọc cả về tốc độ hội tụ lẫn độ ổn định trong quá trình tìm kiếm ma trận trọng số tối ưu W * . Các kết quả đạt được theo hướng tiếp cận này đã được tác giả trình bày trong chương II của luận án. Phần đầu của chương III trình bày ý tưởng của tác giả về việc tách bài toán lọc nhiễu thích nghi nêu trên thành 2 bài toán đơn giản hơn. Đó là bài toán dò tìm tần số của nhiễu và bài toán chọn các hệ số của bộ lọc để giảm thiểu ảnh hưởng suy giảm đến lượng thông tin hữu ích. Các phần tiếp sau của chương sẽ giới thiệu lý do lựa chọn cách tiếp cận mới này, phương pháp giải các bài toán sau khi tách và các kết quả đạt được sau khi tích hợp. Các kết quả của chương này được lấy ở [6] trong Danh mục các công trình của tác giả có liên quan đến luận án.

3.1. Bài toán chọn các hệ số của bộ lọc.

3.1.1. Hàm truyền trong lọc nhiễu đơn tần.

Định nghĩa 3.1. Cho

x(n)

là tín hiệu rời rạc,

X (z )

được gọi là biến đổi z

của x(n) nếu:

trong đó z là biến phức.



X (z)  

n 

x(n)z n ,

Định nghĩa 3.2. Gọi

x(n)

là dãy tín hiệu đầu vào của bộ lọc,

X (z )

là biến

đổi z của

x(n)

theo định nghĩa 3.1. Gọi

y(n)

là dãy tín hiệu đầu ra của bộ

lọc, Y (z )

là biến đổi z của y(n)

theo định nghĩa 3.1. Hàm truyền H (z)

của

bộ lọc được xác định như sau:

H (z)  Y (z) .

X (z)

Nếu thay

z  ei  , vào 2 vế của hàm truyền của bộ lọc, ta có

H (ei  )  Y (ei  ) , trong đó

X (ei  )

i 2  1,

  R1

hoặc được viết dưới dạng:

H ()  Y ()

X ()

là đáp ứng tần số của bộ lọc có hàm truyền H (z) . Đây là 1 kỹ

thuật dùng để khảo sát đáp ứng của bộ lọc đó đối với các tần số khác nhau.

Phần thực của H () phản ánh đáp ứng của bộ lọc về mặt biên độ đối với các

tần số của tín hiệu đầu vào, hay còn gọi là Đáp ứng Biên độ - Tần số. Phần ảo

của H () phản ánh đáp ứng của bộ lọc về pha đối với các tần số của tín hiệu

đầu vào, hay còn gọi là đáp ứng Pha - Tần số (xem [42]).

Trong xử lý tín hiệu, bài toán lọc nhiễu đơn tần được coi như đã được

giải quyết nếu ta tìm được hàm truyền

H (z)

của bộ lọc. Trong [31], hàm

truyền H (z) của bộ lọc triệt tần đã được xác định trong công thức sau:

trong đó

H (z) 

z 2  2z 1 cos 1 1

 2z 2  2z 1 cos 1 1

, (3.1)

1 : Tần số triệt của bộ lọc triệt tần. Bộ lọc có hàm truyền là công thức

3.1 sẽ chặn bất kỳ tín hiệu có tần số

1 . Nếu ta đặt

1  0 , trong đó 0là

tần số của nhiễu (Xem công thức 2.8 và 2.9), thì bộ lọc có hàm truyền cho bởi

3.1 sẽ lọc được nhiễu.

 : Tham số, quyết định độ rộng dải triệt của bộ lọc triệt tần. Độ rộng dải triệt tỷ lệ với độ ảnh hưởng suy giảm tới các tín hiệu hữu ích có tần số lân cận tần số trung tâm 1 .

Độ rộng dải triệt được giải thich như sau: Qua công thức 3.1 ta thấy

rằng

z1,2

 ei 0

được gọi là 2 điểm không (Zero) của hàm truyền

H (z) vì

tại 2 điểm đó thì

H (z)  0 . Hai điểm

p1,2

ei 0

được gọi là 2 điểm cực

của H (z) , vì tại đó H (z)   . Độ rộng dải triệt là tổng khoảng cách giữa 2

cặp điểm không và điểm cực trên mặt phẳng phức.

z1,2

 ei 0

do đó điểm

không nằm trên đường tròn đơn vị, tại góc

0 , vậy ta có công thức tính độ

rộng dải triệt của bộ lọc triệt tần như sau: BW  2(1  ) .

  0.7

  0.8

  0.985

Hình 3.1: Đáp ứng tần số của bộ lọc triệt tần với các giá trị  .

Hình 3.1 minh hoạ sự thay đổi của độ rộng dải triệt trong các trường hợp

khác nhau về độ lớn của  , độ rộng dải triệt rộng nhất khi   0.7 , khi đó

bộ lọc sẽ làm suy giảm đáng kể các tín hiệu có tần số lân cận 1 .

Dựa trên kỹ thuật dò tìm điểm đột biến bằng biến đổi sóng nhỏ và các

phương pháp đạt được độ rộng dải triệt tốt nhất chúng tôi đề xuất lời giải mới

cho trường hợp tần số 0

của nhiễu thay đổi liên tục, phải điều chỉnh các

trọng số của bộ lọc thích nghi sao cho tần số

1 tiến gần đến tần số

0 của

nhiễu với độ rộng dải triệt đủ nhỏ để tránh mất mát các thông tin hữu ích. Chúng tôi đã rời rạc hoá quá trình điều chỉnh trọng số bằng cách coi mỗi điểm rời rạc là một bộ hệ số của lọc triệt tần cố định với hàm truyền có dạng như

trong công thức (3.1). Bây giờ bài toán lọc nhiễu đưa về việc tìm 0

tại

những thời điểm rời rạc và xác định  sao cho độ rộng dải triệt là đủ tốt.

3.1.2. Xấp xỉ hàm truyền trong lọc nhiễu thích nghi

Để giải quyết bài toán xác định tham số  sao cho độ rộng dải triệt là đủ tốt, chúng tôi đề xuất việc xác định độ rộng dải triệt của mô hình lọc nhiễu đơn tần xấp xỉ mô hình lọc thích nghi.

Khi thuật toán LMS dùng cho mô hình lọc nhiễu hội tụ, B. Widrow đã chứng minh trong [44] rằng bộ lọc thích nghi có hàm truyền được mô tả theo công thức

trong đó

H z 

z2  2 cos 0z1  1

1  2C 2z2  21  C 2cos 0z1  1

, (3.2)

 : Kích thước bước thích nghi.

0 : Tần số của nhiễu (xem [26], [28]). Với độ rộng dải triệt cho bởi công thức sau:

trong đó

BW  2C 2 , (3.3)

BW : Độ rộng dải triệt (BandWidth).

 : Kích thước bước thích nghi.

C : Biên độ của nhiễu (xem công thức 2.8 và 2.9).

Khi biểu diễn lại (3.2) dưới dạng

z2  2 cos 0z1  1

H z 

0



1  2C 2z2  21  C 2cos 0z1  1

z 2  2 cos 0z 1  1

1  C 22z 2  21  C 2cos  z1  1

2C 4z 2 z2  2 cos 0z1  1





0



1  2C 2z 2  21  C 2cos 0

z1  11  C 22z2  21  C 2cos 

z 1  1

Chúng tôi nhận thấy rằng, nếu tần số của nhiễu

0 không thay đổi và

 cố định, đủ nhỏ để 2

xấp xỉ 0, hàm truyền của bộ lọc triệt tần thích nghi

sẽ xấp xỉ hàm truyền của bộ lọc triệt tần cố định (3.1) với   1  C 2.

Trong các thực nghiệm với giá trị  =0,05 được coi là đủ nhỏ để đảm bảo hàm truyền lọc nhiễu đơn tần thích hợp với việc xấp xỉ hàm truyền bộ lọc thích nghi và với C  0.5477 , giá trị  = 0,985 < 1 vừa đảm bảo vị trí điểm cực nằm trong đường tròn đơn vị vừa cho ta độ rộng dải triệt đủ tốt.

Từ kết quả thu được ở trên với  , ta có hàm truyền của bộ lọc triệt tần

cố định trong công thức (3.4).

z 2  2z1 cos 0 1

H z 

0.97z2  1.97z1 cos 0

, (3.4)

 1

với bộ hệ số của bộ lọc triệt tần cố định