Kỹ Thuật Làm Nổi Bật Đặc Tính Của Nhiễu Bằng Biến Đổi Fourier.

a0  1 b0  1

a1  2cos0 b1  1.97cos0

a2  1 b2  0.97

3.2. Bài toán dò tần số của nhiễu

Bài toán dò tần số của nhiễu được giải quyết dựa trên cơ sở kết hợp giữa kỹ thuật làm nổi bật đặc tính của nhiễu bằng biến đổi Fourier và kỹ thuật xác định điểm đột biến qua biến đổi sóng nhỏ.

3.2.1. Kỹ thuật làm nổi bật đặc tính của nhiễu bằng biến đổi Fourier.

Trong phần này chúng tôi sẽ trình bày về mối liên quan giữa tần số 0

của nhiễu với điểm đột biến trên phổ của tín hiệu thu nhận.

Trong xử lý tín hiệu, nếu x(n)

Có thể bạn quan tâm!

Xem toàn bộ 130 trang tài liệu này.



là tín hiệu rời rạc, thoả mãn điều kiện:



n 

x(n)   ,

phép biến đổi Fourier đối với tín hiệu rời rạc x(n)



được định nghĩa như sau:

Trong đó

X()  

n 

x(n)ei n , (3.5)

x(n) : Tín hiệu rời rạc, n  Z .

X() : Kết quả phép biến đổi Fourier đối với x(n) .

i : số ảo, với i 2  1 .

Ta ký hiệu

 x(n)  là toán tử thực hiện phép biến đổi Fourier đối với

x(n) , được định nghĩa theo công thức 3.5. Vì biến đổi Fourier có tính chất tuyến tính nên:

 x1(n)  x2(n)    x1( n)    x2( n) . (3.6)

Định nghĩa 3.3. Nếu ta có

X()

là kết quả của phép biến đổi Fourier đối với

x(n)

theo công thức (3.5) thì

X()

được gọi là phổ Biên độ - Tần số của tín

hiệu x(n) .

Theo [31],

X() 

X(   2k)

với k

 Z . Trong đoạn 0  2 ,

X()

lại có tính chất đối xứng qua  , do vậy phổ của

x(n)

thường được

biểu diễn trong quãng Nyquyst 0   .

Trong xử lý tín hiệu, phổ Biên độ - Tần số của x(n)

được gọi tắt là phổ

của x(n) . Trong bài toán lọc nhiễu từ đường tải điện, nhiễu cần loại bỏ được

ký hiệu là N n , có phổ là N() , trong đó



N()   N(n)   

n 

N(n)ei n .

Theo định nghĩa 3.3, ta có

N()

là phổ Biên độ - Tần số của tín hiệu

N n . Mô hình của nhiễu từ đường tải điện đã được xác định, trong đó nhiễu

chỉ có một tần số duy nhất là

0 . Do vậy

N()  0

duy nhất tại 0 và

N()

 0 với

  0 , điều này được minh hoạ trong hình 3.2.

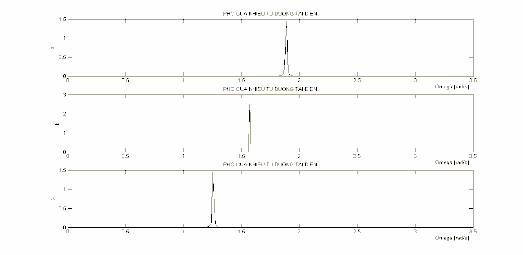
Hình 3.2: Phổ của nhiễu từ đường tải điện.

Với tần sô lấy mẫu là 166 sample/s, hình 3.2, hình a là phổ của nhiễu có tần

số f0

 50.15Hz

tương ứng với

0  1.89 rad / s . Hình b là phổ của nhiễu

có tần số

f0  42.5Hz

tương ứng với

0  1.60 rad / s . Hình c là phổ của

nhiễu có tần số

f0  33Hz

tương ứng với

0  1.25 rad / s . Ta có thể thấy

rằng,

N()

có dạng đột biến tại 0 .

Ta ký hiệu thu được :

NoisyECG n

là tín hiệu điện tim bị nhiễm nhiễu mà ta

trong đó

Nn

NoisyECG n S n N n, (3.6) là nhiễu cộng tính từ đường tải điện ảnh hưởng lên tín hiệu

điện tim và S n là tín hiệu điện tim sạch. Biến đổi Fourier đối với S n ta



được

S()   S(n)   

n 

S( n)ei n . Khi đó

S()

, là phổ của

Sn

được biểu diễn trong hình (3.3).

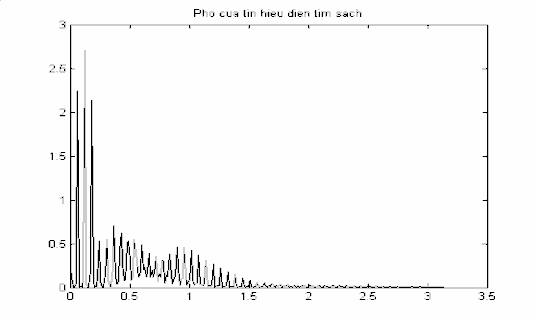
Hình 3.3: Phổ của tín hiệu điện tim sạch.

Theo công thức 3.6

Sn N n Sn Nn; (3.7)

 NoisyECG()

S( )

 N( )

. (3.8)

trong đó

NoisyECG()

là kết quả biến đổi Fourier của

NoisyECG n . Do

vậy điểm đột biến nhọn tại 0 trong

N()

vẫn bảo tồn được các đặc điểm tại

0 trong

Noi syECG()

. Xem hình (3.4),

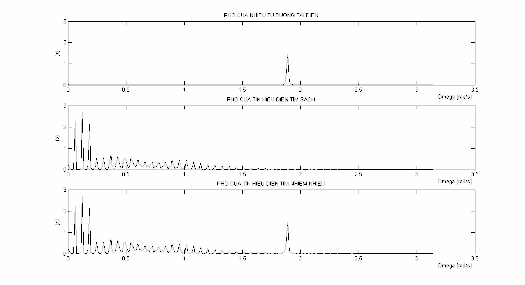
Hình 3.4: So sánh phổ của tín hiệu điện tim nhiễm nhiễu( Noi syECG() ).

Trong hình 3.4 (a) là

N()

, phổ của nhiễu từ đường tải điện. Hình 3.4 (b):

S()

, phổ của tín hiệu điện tim sạch. Hình 3.4 (c):

Noi syECG()

là phổ

của tín hiệu điện tim nhiễm nhiễu từ đường tải điện, trong đó phổ của nhiễu

được phản ánh qua điểm đột biến tại 0 .

Trong xử lý tín hiệu, hàm cửa sổ chữ nhật đối với biến  được định

nghĩa như sau:

Rect L( )

1 0    L



 .

Định nghĩa 3.4. Cho tín hiệu

0   [0, L ]

y() xác định trong khoảng a,b , với

L,   R1 , tín hiệu

smoothed _ y( )

được gọi là kết quả làm trơn đối với

y()

nếu

Smoothed _ y( )  1 y( ) Rect (   ) d  . (3.9)

L  L

Phổ của tín hiệu điện tim sạch hoặc các tín hiệu y sinh sạch không có đỉnh đột biến (xem [3]). Do vậy, để giảm mức độ phức tạp của giải thuật khi phải phân biệt điểm đột biến cần tìm duy nhất với các đột biến không phản

ánh 0 . Chúng tôi đề xuất tiền xử lý bằng cách làm trơn

NoisyECG()

theo

định nghĩa 3.4. Sau khi làm trơn, chỉ còn lại duy nhất điểm đột biến có toạ độ

0 cần tìm (xem hình 3.5).

Đột biến giả, không mang thông tin về 0

Đột biến mang

thông tin về 0

Hình 3.5:Phổ của tín hiệu điện tim sạch (a) và kết quả làm trơn phổ của tín

hiệu điện tim nhiễm nhiễu (b)

Như vậy phép biến đổi Fourier cho phép biểu diễn mối liên quan giữa

tần số riêng của nhiễu 0

với toạ độ của đột biến trong

Noi syECG() và

phép làm trơn

Noi syECG()

vẫn duy trì điểm đột biến tại 0

trong

f () .

Bài toán dò tần số của nhiễu có thể đưa về bài toán xác định toạ độ của điểm đột biến trong phổ của tín hiệu điện tim nhiễm nhiễu hoặc kết quả sau làm trơn của nó.

3.2.2 Kỹ thuật xác định toạ độ điểm đột biến nhọn qua biến đổi sóng nhỏ.

Phần này, chúng tôi sử dụng kỹ thuật xác định toạ độ điểm đột biến đã

được trình bày tại phần 1.3 của luận án để giải bài toán xác định tần số 0

của

nhiễu. Phép biến đổi sóng nhỏ được thực hiện với thang

s  21

cho việc dò

tìm đột biến nhọn, thang

s  22

được sử dụng để tìm các đột biến giả có

dạng gần giống đột biến cần tìm.

f ()

là kết quả làm trơn đối với

Noi syECG() theo công thức (3.9), do vậy qua công thức (1.20) ta có thể

thấy rằng toạ độ điểm đột biến trên

Noi syECG()

sẽ tương ứng với toạ độ

điểm qua không giữa 2 cực đại, cực tiểu cục bộ liên tiếp trên W 1f(s, )

hình 3.6),

(xem

Điểm qua không giữa cực đại dương

và cực tiểu âm liên tiếp

Hình 3.6: Phổ đã được làm trơn của tín hiệu điện tim có nhiễu hình (a) và kết

quả phép biến đổi sóng nhỏ W 1f (s, )

hình (b),

trong đó W 1f (s, )

là phép biến đổi sóng nhỏ sử dụng thang s đối với

f () ,

được định nghĩa trong công thức (1.20). Đồng thời, cặp cực đại - cực tiểu cục

bộ liên tiếp này cũng tương ứng với bộ 3 cực đại - cực tiểu - cực đại cục bộ

liên tiếp trên W 2f (s, )

(xem hình 3.7). Điều này đã được CuiWei Li khẳng

định trong [21] và mở rộng áp dụng sang lớp bài toán phân biệt các đột biến

khác nhau.

Để giảm thiểu mức độ phức tạp tính toán, các tác giả trong [15], [16],

[21] và [23] đều thực hiện biến đổi sóng nhỏ một cách tương đương qua sử dụng các bộ lọc số.

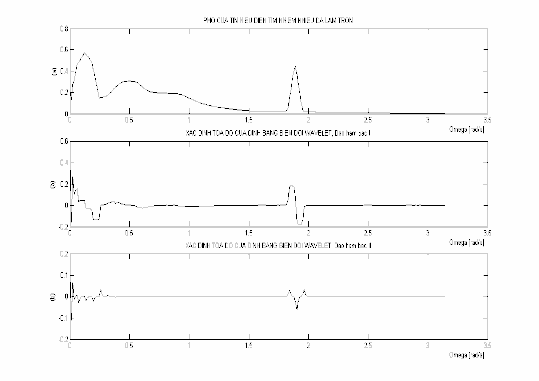
Hình 3.7: Phổ đã được làm trơn của tín hiệu điện tim có nhiễu hình (a) và kết

quả phép biến đổi sóng nhỏ W 1f (s, )

hình (b). và W 2f (s, )

hình (c)

3.2.3. Chọn thang s cho biến đổi sóng nhỏ

Khi sử dụng phép tính xấp xỉ đạo hàm để tìm toạ độ điểm đột biến trên hàm số, độ chính xác có thể giảm nếu đột biến cần tìm nằm xen lẫn với các đột biến có dạng khác mà sự khác biệt không quá lớn. Do vậy, yêu cầu nâng cao độ chính xác đã sớm thu hút được sự chú ý của các nhà khoa học, trong đó các kết quả được CuiWei Li và các đồng sự công bố trong [21] đã tỏ ra

phù hợp để giải quyết bài toán xác định toạ độ điểm đột biến trên f () , là phổ

của tín hiệu nhiễm nhiễu nêu trên. Lời giải này dựa trên đề xuất một tiếp cận cho việc chọn được thang phù hợp cho biến đổi sóng nhỏ để giải quyết vấn đề vừa nêu. Các kết quả trong [21] có thể được tóm tắt như sau. Từ định nghĩa của phép biến đổi sóng nhỏ (công thức 1.13), độ phân giải của phép phân tích

phụ thuộc vào tham số s của hàm

 x . Do vậy, nếu ta chọn được

thang s sao cho độ rộng của

x  

gần nhất với độ rộng của đột biến

mang thông tin hữu ích thì có thể loại bỏ các đột biến không mang thông tin thông qua phép biến đổi sóng nhỏ. Quan sát dạng của đột biến cần tìm toạ độ trong hình 3.7(a), Chúng tôi nhận thấy rằng bài toán xác định toạ độ điểm đột biến trong phổ của tín hiệu điện tim nhiễm nhiễu tương đương với bài toán xác định toạ độ đỉnh R của dãy tín hiệu điện tim mà CuiWei Li đã giải quyết trong [21]. Do vậy chúng tôi có ý định sử dụng các kết quả đã đạt được trong việc chọn thang của CuiWei Li cho bài toán của mình. Các kết quả thực nghiệm sau đó đạt được khá tốt, đáp ứng yêu cầu về độ chính xác, đồng thời có độ phức tạp tính toán thấp. Vì các kết quả nghiên cứu trong [21] đều nhằm đạt đến các thủ tục tính toán trên tín hiệu rời rạc, do vậy một số định nghĩa về xử lí tín hiệu rời rạc được nhắc tới sau đây:

Định nghĩa 3.5. Gọi

x(n)

và y(n)

tương ứng là tín hiệu đầu vào và đầu ra

của bộ lọc số, bk

với

k  0,1...L

là các hệ số của bộ lọc. Nếu