Phương Pháp Thích Nghi Lọc Nhiễu Điện Áp Cho Các Tín Hiệu Y Sinh

Đầu vào chính

S(n)  N(n)

Đầu ra của bộ lọc triệt tần thích nghi

+



- (n)

Có thể bạn quan tâm!

• Can Nhiễu Ảnh Hưởng Đến Chất Lượng Ghi Tín Hiệu Điện Tim
• Bài Toán Xác Định Ma Trận Trọng Số Tối Ưu Cho Tổ Hợp Thích Nghi
• Cơ Sở Toán Học Của Phương Pháp Thích Nghi Dựa Trên Thuật Toán
• Kết Quả Lọc Nhiễu Đối Với Tín Hiệu Điện Não
• Sự Thay Đổi Kích Thước Bước Dựa Trên Giá Trị Tuyệt Đối Của Gradient
• Mse Trường Hợp   0.05 ,   0.5 Và  Thay Đổi.

Xem toàn bộ 130 trang tài liệu này.

Đầu vào tham chiếu

Dịch pha 900

x1(n)

x2(n)

w1(n)

w2(n)

y(n)

+

+ 

Thuật toán LMS

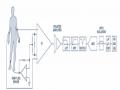
Hình 2.2:Bộ lọc triệt tần thích nghi.

Tín hiệu tham chiếu được xác định là thuần cos ([13], [44]), với L  2 sẽ là

NRn,1 x1n C cosn0, (2.8)

0

N Rn,2  x2n  C sin n0, (2.9) trong đó 0là tần số của nhiễu N (n) , n  Z . Dễ thấy rằng x2n là tín hiệu x1n được làm trễ pha 90 .

Trong [44], B. Widrow đã chỉ ra rằng : Mô hình lọc được mô tả qua

hình 2.2 sẽ tương đương với bộ lọc triệt tất cả tín hiệu đầu vào có tần số 0

mỗi khi thuật toán LMS trong mô hình đó hội tụ. Tần số 0

chính là tần số

của nhiễu, khi đó tín hiệu nhiễu sẽ được khử tại đầu ra. Khi tần số

0 của

nhiễu thay đổi một cách ngẫu nhiên, 2 trọng số

w1 và w2

được chỉnh dần sao

cho sau khi thuật toán tái hội tụ, bộ lọc với cấu trúc mới lại tiếp tục triệt các tín hiệu có tần số trùng với tần số mới của nhiễu. Ngoài ưu điểm tự điều chỉnh, thích nghi với sự thay đổi của nhiễu, bộ lọc triệt tần thích nghi được đánh giá cao nhờ có khả năng giảm nhỏ sự suy giảm, ảnh hưởng đến các tín

hiệu hữu ích có tần số lân cận

0 . Các tần số nằm trong phạm vi ảnh hưởng

được xác định nằm trong dải

[0 C 2, 0 C 2], trong đó  là kích

thước bước của thuật toán LMS (xem công thức 1.11), C là biên độ của nhiễu tại đầu vào tham chiếu (xem công thức 2.8 và 2.9). Do vậy, nếu ta chọn  nhỏ, thuật toán LMS chắc chắn sẽ hội tụ, nhiễu sẽ bị khử tại đầu ra. Đồng thời các tín hiệu hữu ích ít bị ảnh hưởng suy giảm, nhưng sẽ cần nhiều thời gian cho thuật toán LMS hội tụ.

2.1.5. Dãy trọng số lọc W (n)  trong thuật toán LMS

Dãy trọng số lọc

Wnsử dụng trong lọc tín hiệu

Sn N n

được Widrow (xem [44]) và các tác giả khác (xem [2], [3], [10], [17]) đưa ra dưới dạng phương trình sai phân

W n  1  W (n)  2(n)N Rn

 k ,

k  1,..., L , (2.10)

trong đó  là kích thước bước. Dãy

Wn

hội tụ khi kích thước bước

thoả mãn điều kiện trong công thức (1.11) hoặc

0  1

max



. Ở đây  là

max

giá trị riêng lớn nhất của ma trận tự tương quan E[N R (n)N R(n)T ]

tham chiếu. Hoặc thoả mãn điều kiện trong công thức (1.11).

tại đầu vào

Trong mô hình bộ lọc triệt tần với dãy tín hiệu tham chiếu

x1 n ,x2 n , tín hiệu ra

Sˆn

sẽ được ký hiệu thay thế bởi

 n . Bộ

trọng số lọc w1n,w2n được xác định bởi hệ phương trình sai phân

w1n  1 w1n  2 n x1n , (2.11)

w2n 1 w2n 2 nx2n. (2.12)

Trong trường hợp nhiễu từ đường tải điện ảnh hưởng lên tín hiệu y sinh, tín hiệu tham chiếu được chọn ở dạng các hàm số sin và cos (xem công thức (2.8)-(2.9):

x n  C cosn  C cos 2f n  C cos 2n

(2.13)

1 0 0 N

x n  C sin n  C sin 2f n  C sin 2n

(2.14)

2 0 0 N

Ở đây N là số lượng mẫu trong một chu kỳ của tín hiệu tham chiếu của các hàm số sin và cos với các phần tử của ma trận tự tương quan .



1 N 2k 2k 1

2

E x 2(n)  

C 2 sin sin

N k 1 N N

 C 2 , (2.15)

2

2 1 2 N

2k

2k 1 2

E x1(n)   N C

cos

N

k 1

cos N

 2C

, (2.16)

1 N 2n

2n

E  x1 n x2 n  

C 2  cos sin

 0 . (2.17)

Theo (1.9) ta có

N n 1 N N

x 2n 

1

 

1

2

x1 n x2 n   C 0 

R  E     2  , (2.18)





1

 x n x

n

x2n  2

 2 1 2

  0 C 

 2 

với các giá trị riêng (xem [44]) là nghiệm của phương trình

det R I 0 , (2.19)

trong đó I là ma trận đơn vị. Do vậy ta có:







C 2

,

0 21

C 2

2

(2.20)

Thay các giá trị riêng vừa tìm được vào 0  1



(xem [44]) ta có

thể xác định điều kiện để dãy Wn hội tụ là :

max

0  2

C 2

(2.21)

2.2. Phương pháp thích nghi lọc nhiễu điện áp cho các tín hiệu y sinh

Các mô tả toán học ở phần đảm bảo toán học cho phép áp dụng mô hình lọc nhiễu cho các tín hiệu y sinh có biên độ nhỏ để xây dựng các phần mềm nhúng trong lọc nhiễu điện áp đối với các tín hiệu y sinh. Chẳng hạn sóng điện tim có biên độ có biên độ nhỏ, đỉnh lớn nhất cũng chỉ cỡ 1.5  2mV (xem[37]).

Các phần mềm nhúng được viết trên Matlab và có thể mô tả tóm lược như sau.

Phần mềm nhúng được xây dựng dựa trên mô hình bộ lọc triệt tần thích

nghi để thực hiện lọc nhiễu N n 

ra khỏi dãy tín hiệu y sinh thu nhận được

S(n)  N(n) . Việc lọc nhiễu thực hiện bằng cách ước lượng

Nn

thông

L

 2

qua tính

N (n)  wk(n)N Rn, k 

k 1

sao cho

lim

n 

E N(n)  N(n) 

 0 .

Thuật toán lọc được thực hiện thông qua các hàm, do vậy có thể dễ dàng thay đổi giá trị của kích thước bước cho phù hợp với yêu cầu của người sử dụng về tốc độ hội tụ, độ ổn định. Hiện nay chúng tôi gợi ý chọn giá trị kích thước

bước

  0.05

trong trường hợp môi trường nhiễu thay đổi chậm và yêu cầu

cao về chất lượng tín hiệu sau lọc cũng như độ ổn định. Khi môi trường nhiễu

luôn thay đổi kích thước bước

  0.5

tỏ ra phù hợp nhất, thuật toán có khả

năng hội tụ rất nhanh. Nhưng độ ổn định và chất lượng tín hiệu sau lọc không

tốt bằng trường hợp   0.05 . Trường hợp kích thước bước thay đổi dành

cho nhiễu phát sinh từ nguồn điện của máy phát với tần số của nhiễu có dải thay đổi rộng và tốc độ thay đổi lớn. Với ưu điểm thuật toán đơn giản, phần mềm nhúng lọc nhiễu cho tín hiệu y sinh có thể được sử dụng cho cả mục đích đào tạo.

Kết quả thử nghiệm hoạt động của các phần mềm nhúng cho phép tìm ra các tham số phù hợp và được minh hoạ trong các thực nghiệm trình bày ở mục tiếp sau.

2.2.1. Kết quả lọc nhiễu đối với tín hiệu điện tim

2.2.1.1.Trường hợp 1: Kích thước bước thích nghi được chọn cố định

  0.05

Như ta thấy trên hình 2.3 (a), trong trường hợp   0.05 , thuật toán

hội tụ chậm nhưng có độ ổn định tốt, phản ánh qua các dao động của MSE.

MSE trong trường hợp   0.05

MSE trong trường hợp   0.5

E S(n) N(n)  N(n)   trường hợp   0.05

 

 

E S (n) N (n)  N(n)   trường hợp   0.5

 

 

Hình 2.3: MSE trong trường hợp   0.05 và   0.5 .

Kết quả của phép tính

E S(n) N (n)  N(n)  

tương ứng với

  0.05

   

   

được phản ánh trong hình 2.3(b), qua đó ta thấy rằng điều kiện cần và đủ

trong công thức (2.5) là

lim

n 

E S(n) N(n)  N( n)    0

được thoả mãn.

Tốc độ hội tụ và độ ổn định cũng được thấy rõ qua lượng nhiễu còn lại nhiều

trong tín hiệu sau lọc trên hình 2.4.

Tại các pha sau đó (Hình 2.5, 2.6 và 2.7) lượng nhiễu còn lại trong tín hiệu sau lọc giảm nhanh chóng và sự ổn định của thuật toán phản ánh qua độ mấp mô của MSE và tín hiệu sau lọc thể hiện trong các hình trên.

Có thể nhận thấy tốc độ hội tụ của thuật toán trên hình 2.4 và hình 2.5 có sự giảm dần đều đối với lượng nhiễu còn lại trong tín hiệu sau lọc. Điều này hoàn toàn phù hợp với kết quả rút ra từ hình 2.3.

Bắt đầu lọc nhiễu

Tại đây, nhiễu đã giảm

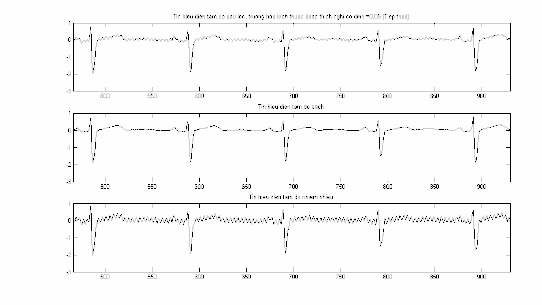
Hình 2.4: So sánh S(n) với  n trong đoạn n  1  465 .

Nếu so sánh tín hiệu điện tim sạch (hình giữa) và tín hiệu điện tim thu được bị nhiễm nhiễu (hình dưới cùng). Ta có thể thấy rằng tại đầu thu được của tín hiệu điện tim, nhiễu đã làm mất đi các thông tin vốn hữu ích cho việc chẩn đoán tại các đỉnh sóng P, Q, S và T.

Trong pha tiếp theo của hình 2.6, ta thấy trong tín hiệu sau lọc, lượng nhiễu còn lại rất nhỏ và ta có thể nhận ra hình dạng của các đỉnh sóng P, Q, S, T.

Hình 2.5: So sánh S(n) với  n trong đoạn n  466  930 .

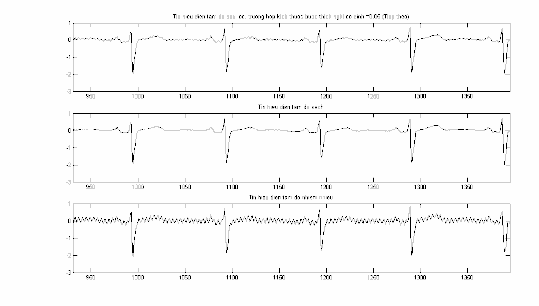
Hình 2.6: So sánh S(n)

với  n trong đoạn n  931  1395

Hình 2.7: So sánh S(n)

với  n trong đoạn n  1396  1860 .

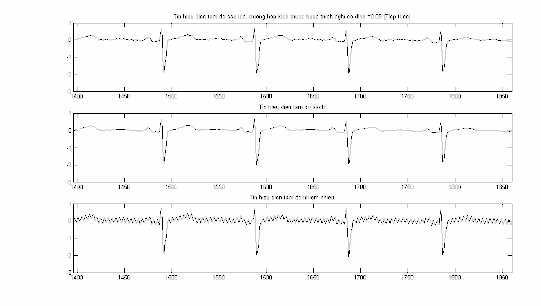
Trong hình 2.7 tiếp theo, qua so sánh tín hiệu điện tim sau lọc với tín hiệu điện tim sạch tương ứng (hình giữa) có thể thấy rằng tín hiệu điện tim sau lọc giống hệt tín hiệu điện tim sạch tương ứng. Điều này hoàn toàn phù hợp với đường biểu diễn các giá trị của sai số trung bình bình phương trong hình 2.3, khi các giá trị MSE tiến rất gần 0 sau 1800 vòng lặp. Ta có thể nói

rằng tín hiệu sau lọc

(n)

tiến đến xấp xỉ tín hiệu điện tim sạch

Sn

sau

một số hữu hạn các vòng lặp.

Có thể thấy việc chọn kích thước bước cố định

  0.05

cho ta tín

hiệu sau lọc có chất lượng rất cao, nhưng số bước lặp để thuật toán hội tụ cũng tăng theo. Điều này khiến yêu cầu giảm thời gian hội tụ cho thuật toán không đạt được.

2.2.1.2. Trường hợp 2: Kích thước bước thích nghi đươc chọn cố định

  0.5

Trên hình 2.3(a), trường hợp

  0.5

MSE cho ta thấy thuật toán có

tốc độ hội tụ rất nhanh. Điều này được phản ánh qua tốc độ giảm về không