Cơ Sở Toán Học Của Phương Pháp Thích Nghi Dựa Trên Thuật Toán

thức (1.15) ta thấy rằng

triệt tiêu bậc 2 .

1(x) có moment triệt tiêu bậc 1 ,

2(x)

có moment

Sử dụng các công thức (1.14), (1.16), (1.17), (1.18) và (1.19) để thực



Có thể bạn quan tâm!

Xem toàn bộ 130 trang tài liệu này.

hiện biến đổi sóng nhỏ tại thang s đối với

fx bằng 1x ta có



1 1 

ds x 

W f s,x  f * sx  f * s



dx 

trong đó

 s df dx

* s

x , (1.20)

W1fs,x  : Biến đổi Sóng nhỏ đối với

nhỏ Gauss1.

fx tại thang s , sử dụng sóng

1(x)

: Sóng nhỏ Gauss1.

 x  1 x: Sóng nhỏ cơ sở Gauss được dãn ở thang s .

s s  s 

f (x) * s( x) : Được coi là phép làm trơn f (x) bằng s (x) .

Tương tự, thực hiện biến đổi sóng tại thang s đối với

2x ta có

fx

bằng

2 2 

2 d 2s x 

W f s,x  f

*sx f

* s







dx 2 

 s2

d2 f dx 2

* s

x

(1.21)

Công thức (1.20) và (1.21) có ý nghĩa rằng: Thực hiện biến đổi sóng

nhỏ đối với

fx

bởi các hàm sóng nhỏ có moment triệt tiêu bậc 1 và 2 tại

thang s sẽ tương đương với việc tính đạo hàm bậc 1 và 2 của hàm

được làm trơn bằng s x .

1.3.2. Tìm điểm đột biến nhọn.

fx đã

Để tìm toạ độ của điểm đột biến, hướng tiếp cận sử dụng các toán tử tính xấp xỉ hàm đã tỏ rõ ưu điểm về độ chính xác cao và độ phức tạp tính toán thấp. Nếu các đột biến đồng nhất về dạng, ta có thể sử dụng các toán tử giả đạo hàm như Canny, Sobel, Robert để tính đạo hàm bậc 1 và 2. Tuy nhiên, trong trường hợp, khi phải tìm toạ độ của 1 loại đột biến nằm xen lẫn với nhiều dạng đột biến khác. Khi đó không thể sử dụng các kỹ thuật trên. Bài toán này dẫn đến việc tìm kỹ thuật mà cho phép chỉ xác định toạ độ của đột biến mang thông tin mà ta quan tâm, đồng thời bỏ qua các đột biến không cần thiết. Để giải quyết vấn đề này, từ năm 1992, S. Mallat đã đề xuất sử dụng công thức 1.20 và 1.21 làm cơ sở cho toán tử giả đạo hàm sử dụng biến đổi sóng nhỏ đa thang. Điều này cho phép loại bỏ các đột biến không mang thông tin cần tìm nếu chọn được thang phù hợp. Tiếp tục nghiên cứu theo hướng này, năm 1994, CuiWei Li trong [21] đã công bố các kết quả đạt được trong việc chọn thang cho một số dạng đột biến đặc trưng, trong đó có dạng mà chúng tôi gặp phải khi giải quyết bài toán dò tần số của nhiễu tại chương 3 trong luận án này. Các kết quả trên được tóm tắt như sau:

Định nghĩa 1.3. Cho hàm số

f (x)

xác định trên [a,b]. Hàm

g(x)  W 1f 2, x 

xác định trên [a,b]. Đoạn

[a1,b1 ]

thoả mãn

a  a1  b1  b . Điểm

x0  [a1,b1 ]

được gọi là toạ độ đỉnh của đột biến

nhọn trên

f (x) , tồn tại trong đoạn [a1,b1 ] nếu với bất kỳ t  [0,1] ta có:

g(ta1 (1  t)x 0)

 tg(a1)

(1  t)g( x 0)

g(tx 0 (1  t)b1)

 tg(x 0)

(1

t)g(b1)

g(x0)  0

Trong [14] và [23], S. Mallat đã chỉ ra rằng : Nếu

f (x)

có đột biến

nhọn tại

x0 , phép làm trơn

f (x)

sử dụng tích chập

f (x) *

s( x)

sẽ bảo tồn

tính đột biến của

f (x)

tại x0 . Do vậy việc xác định toạ độ điểm đột biến nhọn

trên

f (x)

sẽ tương đương với việc dò điểm đột biến trên kết quả của phép tích

chập giữa

f (x)

và s (x) . Qua công thức (1.20) và (1.21), ta thấy rằng đối với

thang s cố định, W 1fs,x  và W 2fs,x  tương ứng là toán tử giả đạo hàm

bậc 1 và 2 đối với

f (x) *

s( x) . Do vậy W 1f s,x sẽ đi qua không và đổi dấu

tại

x 0 . Dò tìm các điểm qua không giữa cặp cực đại dương và cực tiểu âm

liên tiếp trên W 1fs,x 

là các thủ tục dò tìm toạ độ điểm đột biến nhọn trên

f (x) . Bộ ba cực đại dương, cực tiểu âm, cực đại dương của W 2f s,x được sử dụng để kiểm chứng độ chính xác của kết quả dò tìm. Ngay sau đó 2 năm, CuiWei Li đã công bố trong [21] kết quả đạt được về chọn thang s cho bài toán tìm toạ độ các đột biến có dạng đỉnh nhọn, là dạng đột biến tương đồng với đột biến trong bài toán của chúng tôi. Các kết quả trên đã cho chúng tôi những kỹ thuật cần thiết để giải quyết bài toán lọc nhiễu từ mạng điện. Trong đó phần khó khăn nhất là yêu cầu độ chính xác cao khi xác định tần số của nhiễu, tránh bị nhầm với tần số của thông tin khác nằm lân cận đó. Với đặc điểm đơn tần của nhiễu, chỉ tập trung tại 1 tần số nên có thể biểu diễn nhiễu như là điểm đột biến mà vị trí của điểm đột biến này có thể được xác định chính xác qua phép biến đổi sóng nhỏ với thang s được chọn phù hợp.

KẾT LUẬN

Trong chương này, bộ lọc nhiễu thích nghi sử dụng thuật toán LMS đối với bài toán lọc nhiễu tín hiệu y sinh đã được mô tả cùng với các công cụ toán học sử dụng trong các chương sau. Việc xây dựng cơ sở toán học cho các bài toán lọc nhiễu sẽ được giải quyết trong chương 2 của luận án . Chương 3 giới thiệu một tiếp cận khác cho phép giải quyết bài toán lọc nhiễu với dữ liệu đầu vào không dừng.

Chương 2

Lọc nhiễu bằng các phương pháp thích nghi dựa trên thuật toán LMS và khả năng tăng hiệu quả bằng một giải pháp thay đổi kích thước bước.

Chương này trình bày mô hình toán của bộ lọc nhiễu thích nghi và đề xuất phương pháp nâng cao hiệu năng của bộ lọc nhiễu thích nghi trên cơ sở điều chỉnh kích thước bước thích nghi cho thuật toán LMS.

Toàn chương được chia làm ba phần chính. Phần 1 trình bày mô hình toán của bộ lọc nhiễu thích nghi. Phần 2 mô tả phần mềm nhúng trong bộ lọc thích nghi xử lý nhiễu điện áp trên tín hiệu điện tim và điện não. Phần 3 trình bày thuật toán LMS với kích thước bước thích nghi thay đổi và so sánh với trường hợp thuật toán LMS với kích thước bước thích nghi cố định.

Các kết quả của chương này được lấy trong các bài báo [1-5] và [7] trong Danh mục các công trình của tác giả có liên quan đến luận án.

2.1. Cơ sở toán học của phương pháp thích nghi dựa trên thuật toán

LMS trong lọc nhiễu.

2.1.1. Phát biểu bài toán

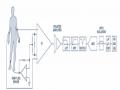
Mô hình lọc nhiễu cộng tính trong tín hiệu y sinh (xem [3],[7],[8],[17], [18], [20], [29] và [34]) được mô tả trong hình 2.1. Trong mô hình này ECG n là dãy tín hiệu y sinh bị nhiễu tại đầu vào và đã rời rạc hoá. S n là dãy tín hiệu y sinh sạch và N n là dãy tín hiệu nhiễu.

W (n)  wk(n), k  1,..., L  là dãy trọng số,

N R (n)  N R n, k , k

 1,..., L 

là dãy tín hiệu tham chiếu giúp tạo thành

tổ hợp tuyến tính bậc L . Trong bài toán này, N R (n)

công thức 1.7.

tương đương

X (n)

của

N(n)  wl(n)N Rn, l . (2.1)

l 1

N(n)

tương đương y(n)

trong công thức (1.5).

ECG n S n N n



Nn

S(n) S(n)

NRn

w1 n + 

Z-1

+ +

w2 n 

Thuật toán LMS

Z-1

wL n 

Hình 2.1: Mô hình thích nghi của bộ lọc nhiễu.

Ký hiệu: S(n) tương đương (n)

hình lọc nhiễu này

trong bài toán xác định W * , trong mô

S(n)  S(n)  N( n)  N( n) , (2.2) mục tiêu đặt ra là có được dãy Wn và dãy NRnđể

lim E N n  Nn 2

 0 , (2.3)

n   

từ dãy W n và dãy N Rn thoả mãn điều kiện

lim

n 

E S2





n   0





(2.4)

của thuật toán LMS đối với tín hiệu cộng tính S n  N n .

2.1.2. Cơ sở toán học của mô hình lọc nhiễu

Định lý: Giả sử dãy Wn và NRn

thoả mãn điều kiện (2.4). Khi ấy

điều kiện cần và đủ để chúng thoả mãn điều kiện (2.3) là

   

Chứng minh:

lim

n 

E S(n) N(n)  N( n)    0 . (2.5)

Điều kiện cần: Từ bất đẳng thức

E S (n) N (n)  N(n)    E S( n) N( n)  N( n)  

       

E S 2(n) 

E N(n)  N(n) 2





 ,

suy ra rằng nếu

lim E N n  Nn 2 0

thì lim E S n N n  Nn    0

đối

n  

 n   

 

với dãy tín hiệu S n  có E  S 2 n 

giới nội.

 

Để áp dụng kết luận này cho việc chứng minh từ (2.3)-(2.4) suy ra

(2.5), để ý rằng

 2  2

  

  

 2

E  S

(n)   E S

(n)   2E S(n) N( n)

 N( n)    E N( n)

 N( n) 

(2.6)

và điều kiện (2.4) là trường hợp riêng của dãy tín hiệu có moment bậc II giới

nội nên

Sn

cũng là dãy có moment giới nội. Áp dụng kết luận trên cho

Sn và (2.3) suy ra (2.5) đúng và điều kiện cần được chứng minh.

Điều kiện đủ:

Giả sử

WnvàNRnthoả mãn điều kiện (2.4) và (2.5). Khi đó (2.6)

kéo theo (2.3) dựa trên bất đẳng thức

 2

 2

  

lim E N n  N n 

 lim S

n   2 lim E S n N n  N n 

n   

n  

 n 0  

và do đó điều kiện đủ được chứng minh

2.1.3. Đánh giá sai số trung bình bình phương.

Kết quả lọc được đánh giá bằng sai số trung bình bình phương sau Q

bước

1 Q  2

Ở đây

MSE

 S (n)  S(n)

n 1

. (2.7)

S n là giá trị của tín hiệu y sinh sạch thứ n

Snlà tín hiệu y sinh sau lọc thứ n .

Tốc độ hội tụ của thuật toán được phản ánh qua tốc độ hội tụ về xấp xỉ 0 của MSE. Độ ổn định của thuật toán được phản ánh thông qua sự thay đổi của MSE sau khi thuật toán đã hội tụ (xem [22], [39]).

2.1.4. Tín hiệu tham chiếu Widrow N R n trong thuật toán lọc LMS.

Dãy tín hiệu tham chiếu

nghi mô tả trong hình dưới đây.

NRn

được chọn từ bộ lọc triệt tần thích