của MSE nhưng có độ ổn định không tốt, phản ánh qua trạng thái dao động của MSE sau vòng lặp thứ 180 và lượng nhiễu còn lại trong tín hiệu sau lọc trên các hình từ 2.8 đến 2.11. Đồng thời, qua hình 2.3(c) ta cũng thấy rằng điều kiện trong công thức (2.5) không được thoả mãn khi
lim
n
E S(n) N(n) N( n) 0 . Điều này cho phép giải thích lý do của
tình trạng không ổn định của thuật toán LMS dùng kích thước bước lớn cho các ứng dụng lọc nhiễu.
Trong trường hợp 1, khi kích thước bước thích nghi được chọn cố định
0.05 , sau khi hội tụ, nếu nhiễu không thay đổi thì kết quả lọc rất ổn
Có thể bạn quan tâm!
-
Bài Toán Xác Định Ma Trận Trọng Số Tối Ưu Cho Tổ Hợp Thích Nghi -
Cơ Sở Toán Học Của Phương Pháp Thích Nghi Dựa Trên Thuật Toán -
Phương Pháp Thích Nghi Lọc Nhiễu Điện Áp Cho Các Tín Hiệu Y Sinh -
Sự Thay Đổi Kích Thước Bước Dựa Trên Giá Trị Tuyệt Đối Của Gradient -
Mse Trường Hợp 0.05 , 0.5 Và Thay Đổi. -
Thay Đổi, Eeg Trước Và Sau Lọc Nhiễu, Đoạn N 2001 3000 .
Xem toàn bộ 130 trang tài liệu này.
định. Trong trường hợp 2, 0.5 , sau khi hội tụ, thuật toán vẫn không ổn
Bắt đầu lọc
Tại đây, nhiễu đã giảm đáng kể
định. Điều này cũng được phản ánh qua quan sát thấy lượng nhiễu còn lại trong tín hiệu sau lọc qua việc so sánh tín hiệu điện tim sau lọc (đường trên cùng) với tín hiệu điện tim sạch tương ứng (đường giữa).
Hình 2.8: Với 0.5 , S(n)
và n , trong đoạn n 1 465 .
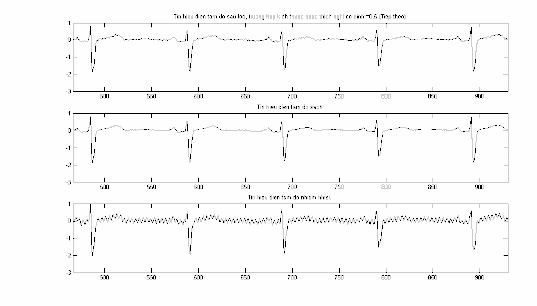
Hình 2.9: Với
0.5 , S(n)
và n , trong đoạn n 466 930 .
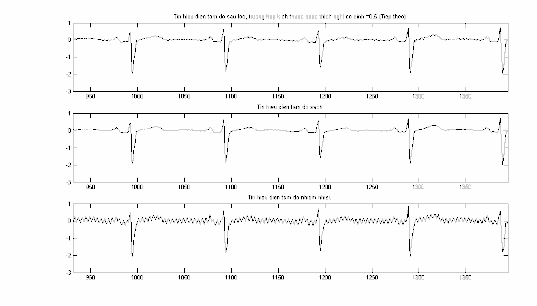
Hình 2.10: Với
0.5 , S(n)
và n , trong đoạn n 931 1395 .
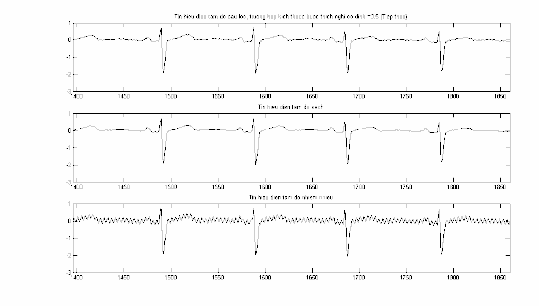
Hình 2.11: Với 0.5 , S(n) và n , trong đoạn n 1396 1860 .
2.2.2. Kết quả lọc nhiễu đối với tín hiệu điện não
2.2.2.1.Trường hợp 1: Kích thước bước thích nghi được chọn cố định
0.05 . Trong trường hợp 0.05 trên hình 2.12(a) cho thấy thuật toán
hội tụ chậm (sau khoảng 2000 vòng lặp). Tính ổn định không cao, được phản ánh qua các dao động của MSE. Để tránh bị che lấp bởi đường cong mô tả MSE trong trường hợp 0.5 , ta có thể quan sát hình 2.13 với MSE trong hai trường hợp được biểu diễn tách rời trên cùng trên một hàng ngang. Với
hình 2.13 ta thấy rằng trong trường hợp 0.5 , MSE có độ dao động bất
thường cao hơn trong trường hợp 0.05 .
Điều này cũng được thể hiện qua lượng nhiễu còn lại giảm dần trong tín hiệu sau lọc trên hình 2.14. Tại pha sau đó (Hình 2.15) lượng nhiễu vẫn tiếp tục giảm và khi ta so sánh tín hiệu điện não sau lọc (Hình trên đỉnh) với tín hiệu điện não sạch (hình giữa) trong các pha sau tại hình 2.16 và 2.17 có
thể thấy lượng nhiễu còn lại trong tín hiệu sau lọc là khá lớn, tín hiệu sau lọc
(n)
chưa ổn định quanh tín hiệu điện não (EEG) sạch S n .
MSE trong trường hợp 0.05
MSE trong trường hợp 0.5
E S (n) N (n) N(n) trường hợp 0.05
E S(n) N(n) N(n) trường hợp 0.5
Hình 2.12: E S(n) N (n) N(n)
trong trường hợp 0.05 và 0.5 .
Thuật toán LMS hội tụ nhưng chưa ổn định không những được phản ánh qua độ mấp mô của MSE và tín hiệu sau lọc trong các hình 2.12(a) mà còn được đánh giá qua điều kiện cần và đủ trong công thức (2.5). Qua hình
2.12(b) và 2.12(c), ta thấy rằng
E S(n) N(n) N(n)
đều không tiến đến
0 khi n , do đó không thoả mãn điều kiện cần và đủ được đề xuất tại công thức 2.5 trong chương 2.
Trên hình 2.14, ta thấy tín hiệu điện não sau lọc tiếp tục tiến gần đến tín hiệu điện não sạch nhiễu. Tại hình 2.16 và hình 2.17, ta thấy tín hiệu điện não sau lọc đã tiến gần đến tín hiệu điện não sạch, tuy nhiên vẫn tồn tại các điểm mất ổn định.
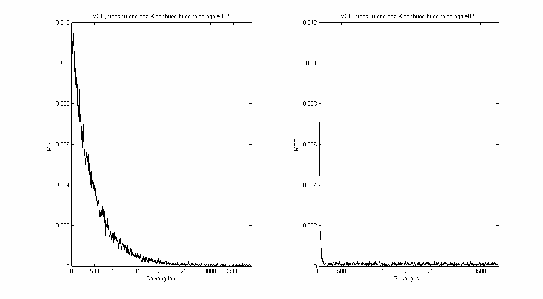
Hình 2.13: MSE trong trường hợp 0.05 và 0.5 .
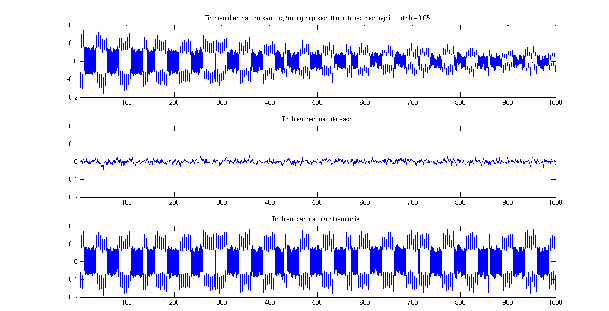
Hình 2.14: Với 0.05 , EEG trước và sau lọc nhiễu, đoạn n 1 1000 .
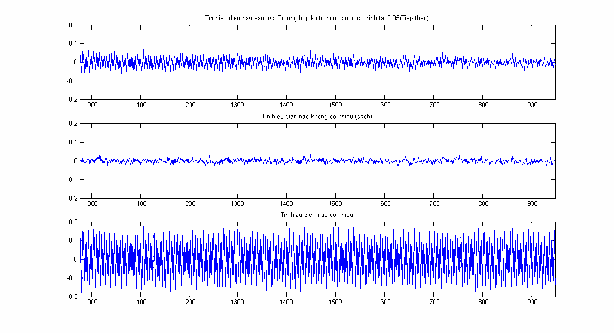
Hình 2.15:EEG trước và sau lọc nhiễu, đoạn n 1001 2000 .
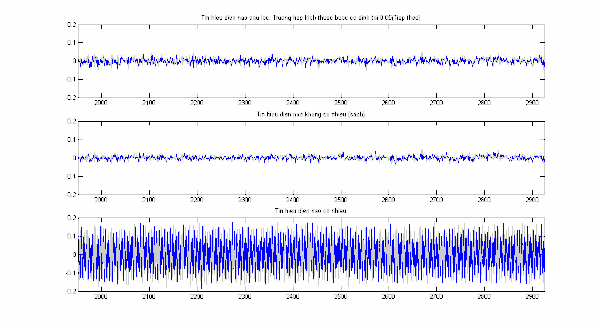
Hình 2.16: EEG trước và sau lọc nhiễu, đoạn n 2001 3000 .
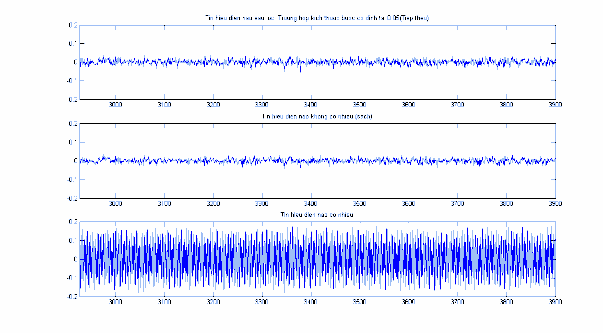
Hình 2.17: EEG trước và sau lọc nhiễu, đoạn n 3001 4000 .
Như vậy, trong trường hợp kích thước thích nghi được chọn cố định tại 0.05 lọc nhiễu của đường tải điện khỏi tín hiệu điện não có tốc độ hội tụ chậm và độ ổn định chưa đủ tốt.
2.2.2.2.Trường hợp 2: Kích thước bước thích nghi được chọn cố định
0.5
Khi kích thước bước thích nghi được chọn cố định 0.5 , MSE
trong hình 2.12 cho thấy tốc độ hội tụ của thuật toán tăng lên rõ rệt. Thuật toán hội tụ sau khoảng 200 vòng lặp. Độ ổn định của thuật toán được phản ánh rõ rệt hơn qua đường cong biểu diễn sai số trung bình bình phương tại
hình 2.13 so với trường hợp bộ lọc có kích thước bước cố định 0.05 .
Một lần nữa ta thấy rằng trong bài toán lọc nhiễu động, khi tăng giá trị của kích thước bước thích nghi, độ ổn định của thuật toán LMS giảm xuống.
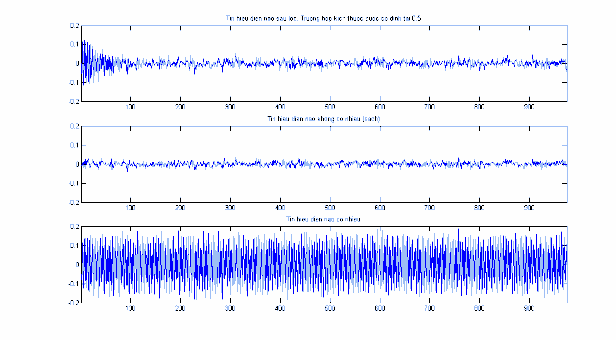
Hình 2.18: Với 0.5 , EEG trước và sau lọc nhiễu, đoạn n 1 1000 .
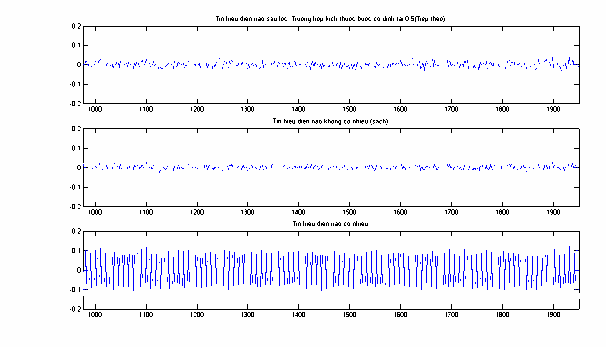
Hình 2.19: EEG trước và sau lọc nhiễu, đoạn n 1001 2000 .