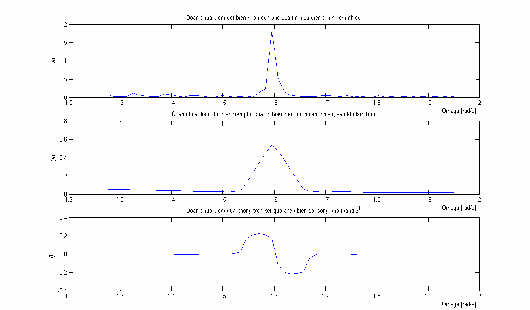
Hình 3.16: Kết quả ước lượng đạo hàm bậc I dùng biến đổi sóng nhỏ s 21
Với tần số
0 1.6 rad / s , điểm không và điểm cực được biểu diễn
trên hình 3.17 dưới đây.
Có thể bạn quan tâm!
-
Kỹ Thuật Làm Nổi Bật Đặc Tính Của Nhiễu Bằng Biến Đổi Fourier. -
So Sánh Kết Quả Phép Biến Đổi Sóng Nhỏ Dùng Các Thangs 21 Và -
Đánh Giá Độ Chính Xác Và Mức Độ Phức Tạp Tính Toán Của Giải Thuật Tìm Tần Số 0 Của Nhiễu. -
Các phương pháp thích nghi trong lọc nhiễu tín hiệu điện tim - 15 -
Các phương pháp thích nghi trong lọc nhiễu tín hiệu điện tim - 16
Xem toàn bộ 130 trang tài liệu này.
Điểm không và điểm cực gần như trùng nhau tại
0
Hình 3.17: Biểu diễn điểm không và điểm cực của H (z)
vị
trên đường tròn đơn
Hình 3.18 cho phép đánh giá đề xuất của chúng tôi về mô hình lọc nhiễu giải thuật tìm tần số. Ta thấy rằng gần như không còn nhiễu trong tín hiệu điện tim sau lọc.
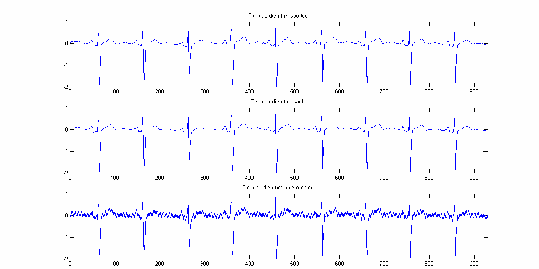
Hình 3.18: So sánh tín hiệu điện tim sau lọc với tín hiệu điện tim sạch.
So sánh tín hiệu sau lọc với tín hiệu sạch trong hình 3.18, ta thấy rằng mô hình lọc nhiễu đề xuất cho phép khôi phục lại tín hiệu sạch với độ trung thực rất tốt. Điều này cũng được phản ánh qua MSE trên hình 3.19
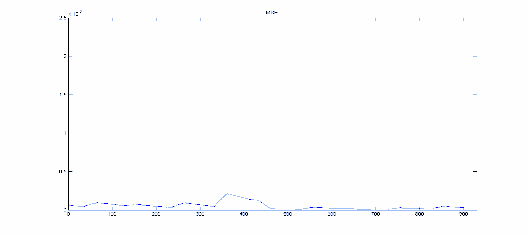
Hình 3.19: MSE giữa tín hiệu sau lọc (n) và tín hiệu điện tim sạch S(n)
Đối với tín hiệu điện não
Tương tự với thực nghiệm 3.1 đối với tín hiệu điện tim, để đánh giá độ
chính xác, chúng tôi sử dụng tín hiệu điện não mô phỏng như là tín hiệu S(n) .
Tín hiệu
N (n)
là nhiễu mô phỏng, có tần số
0 1.5 rad / s . Tín hiệu điện
não nhiễm nhiễu được ký hiệu là NoisyEEG (n ) , trong đó
NoisyEEG (n) S (n) N(n) . Các tín hiệu S(n) ,
được biểu diễn trên hình 3.20 dưới đây.
N (n)
và NoisyEEG (n )
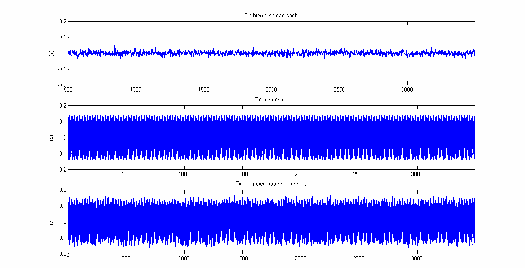
Hình 3.20: Biểu diễn S(n) , N (n)
và NoisyEEG (n )
trong miền thời gian
Chúng tôi sử dụng giải thuật đề xuất để tìm tần số của nhiễu, các bước chính được minh hoạ như sau:
Thực hiện biến đổi Fourier nhanh đối với tín hiệu NoisyEEG (n ) , kết
quả được biểu diễn trong hình 3.21(a). Kết quả phép làm trơn được biểu diễn trong hình 3.21(b). Kết quả của việc sử dụng biến đổi sóng nhỏ tại thang
s 21
để ước tính đạo hàm bậc I đối với phổ đã được làm trơn của
NoisyEEG (n ) , được biểu diễn trên hình 3.21(c). Tương tự, hình 3.21(d) là
kết quả phép biến đổi sóng nhỏ với thang s 22 . Hình 3.21(e) là kết quả của phép tính đạo hàm bậc II sử dụng biến đổi sóng nhỏ tại thang s 21 .
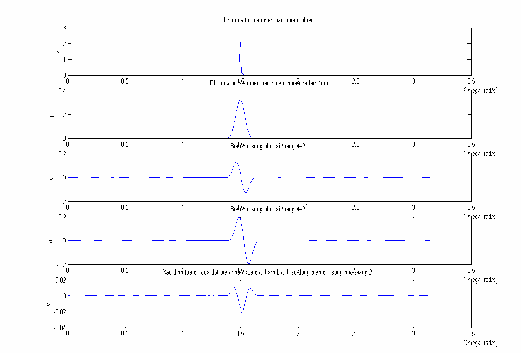
Hình 3.21: Các kết quả chính khi thực hiện giải thuật tìm tần số của nhiễu
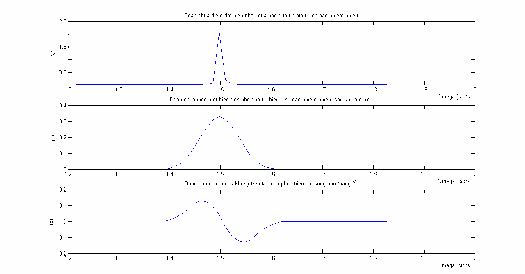
Hình 3.22: Kết quả ước lượng đạo hàm bậc I dùng biến đổi sóng nhỏ thang
21
Toạ điểm đột biến được xác định tại 0
1.5 rad / s . Để thuận lợi cho
việc quan sát kết quả, hình 3.22 sẽ biểu diễn tập trung vào xung quanh tần số của nhiễu.
Với tần số
0 1.5 rad / s , bô lọc triệt tần có đáp ứng Biên độ - Tần
số như trong hình 3.23.
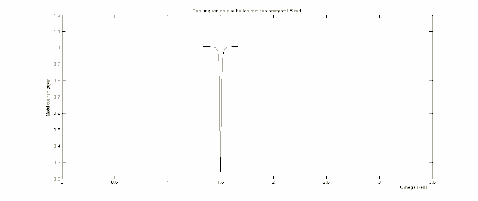
Hình 3.23: Đáp ứng Biên độ - Tần số của bộ lọc với (3.4) và 0
1.5 rad / s
Với tần số
0 1.5 rad , điểm không và điểm cực được biểu diễn trên
hình 3.24 dưới đây.
Điểm không và điểm cực gần như trùng nhau tại
0
Hình 3.24: Biểu diễn điểm không và điểm cực của H (z)
vị
trên đường tròn đơn
Độ chính xác cũng được phản ánh qua MSE trên hình 3.25, và thông
qua so sánh tín hiệu điện não sau lọc trên hình 3.26.
(n)
với tín hiệu điện não sạch
S(n)
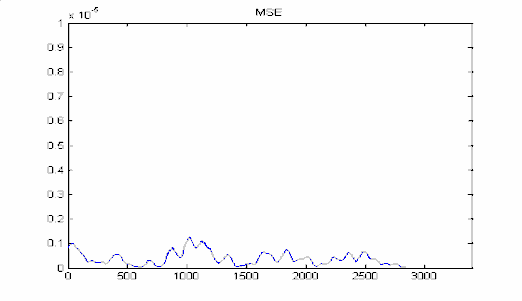
Hình 3.25: MSE giữa tín hiệu sau lọc (n) và tín hiệu điện tim sạch S(n)
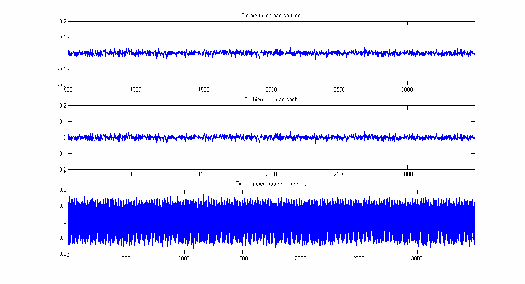
Hình 3.26: So sánh tín hiệu điện não sau lọc với tín hiệu điện não sạch.
3.6. Đánh giá thuật giải sử dụng biến đổi sóng nhỏ
Thuật giải sử dụng biến đổi sóng nhỏ đã được mã hoá và thử nghiệm trên cơ sở dữ liệu của MIH/BIH với nhiễu nhân tạo sử dụng hàm tạo số ngẫu nhiêu với phân bố Gauss. Từ các kết quả thử nghiệm và phân tích, cho thấy giải thuật tìm tần số của nhiễu do chúng tôi đề xuất có những ưu điểm sau: Đối với bài toán lọc nhiễu cho tín hiệu điện tim:
- Nếu tần số của nhiễu nằm ngoài dải 0 0.1rad / s và 0.2 0.3rad / s
thì thuật giải hầu chắc chắn tìm được tần số
0 của nhiễu nhờ việc
thực hiện phép biến đổi Fourier và sóng nhỏ bằng các thuật toán biến đổi nhanh.
- Thuật giải sẽ đạt độ chính xác cao, phản ánh qua độ hẹp của băng tần với độ phân giải không gian tần số thành 255 đoạn trong khoảng từ 0
- Độ phức tạp của thuật giải phản ánh qua quan hệ logarit nhờ áp dụng các thuật toán biến đổi nhanh. Đề xuất tiền xử lý tập dữ liệu cho phép loại bỏ các đột biến giả trước khi thực hiện biến đổi Sóng nhỏ.
- Thuật giải đã sử dụng hiệu quả hai phép biến đổi Fourier và Sóng nhỏ,
cho phép đơn giản hoá mô hình của bộ lọc do không cần dùng đầu vào
tham chiếu (Reference Input) và bộ trễ
triệt tần của B. Widrow.
900
như trong mô hình bộ lọc
- Có thể sử dụng lý thuyết xác suất để tiếp tục đơn giản hoá độ phức tạp
tính toán khi xác định được phân bố của
0 trên trục tần số .
KẾT LUẬN
Trong chương này chúng tôi đã đề xuất mô hình lọc nhiễu từ nguồn cung cấp điện và giải thuật tìm tần số của nhiễu sử dụng kết hợp biến đổi Fourier với biến đổi sóng nhỏ. Đề xuất tiền xử lý tập dữ liệu thông qua làm trơn bằng bộ lọc thông thấp trước khi biến đổi sóng nhỏ đã làm cho thuật giải trở nên dễ thực hiện với độ chính xác cao. Chọn được thang s phù hợp cho phép biến đổi sóng nhỏ sao cho lựa chọn được chính xác thông tin cần quan tâm. Thuật giải đã được thử nghiệm trên Matlab và lời giải được so sánh với các kết quả mới nhất của thuật toán LMS với kích thước bước thay đổi đã cho thấy hiệu quả đáng kể của thuật giải.