So Sánh Kết Quả Phép Biến Đổi Sóng Nhỏ Dùng Các Thangs  21 Và

L

y(n)  bkx(n  k) , với L

k 0

xung hữu hạn bậc L .

 Z 

thì bộ lọc được gọi là bộ lọc đáp ứng

Có thể bạn quan tâm!

• Mse Trường Hợp   0.05 ,   0.5 Và  Thay Đổi.
•  Thay Đổi, Eeg Trước Và Sau Lọc Nhiễu, Đoạn N  2001  3000 .
• Kỹ Thuật Làm Nổi Bật Đặc Tính Của Nhiễu Bằng Biến Đổi Fourier.
• Đánh Giá Độ Chính Xác Và Mức Độ Phức Tạp Tính Toán Của Giải Thuật Tìm Tần Số 0 Của Nhiễu.
• Kết Quả Ước Lượng Đạo Hàm Bậc I Dùng Biến Đổi Sóng Nhỏ S  21
• Các phương pháp thích nghi trong lọc nhiễu tín hiệu điện tim - 15

Xem toàn bộ 130 trang tài liệu này.

Định nghĩa 3.6.

(n)

được gọi là xung Dirac nếu: (n)  1

0

n  0

n  0

Định nghĩa 3.7 Cho bộ lọc đáp ứng xung hữu hạn bậc L , nếu

L

x(n)  (n)

thì h(n) 

bk(n  k)

k 0

được gọi là đáp ứng xung của bộ lọc.

Trong bài toán xác định toạ độ đỉnh sóng R trên biến n (xem hình 1.1), vấn đề chọn thang được giải quyết dựa trên tiếp cận như sau : Phép biến đổi sóng nhỏ trên 1 dãy số tương đương với việc thực hiện nhân chập dãy số đó với đáp ứng xung của 1 bộ lọc số (công thức 1.17). Do vậy phép biến đổi sóng nhỏ sẽ mang tính chọn lọc thông tin hữu ích nếu bộ lọc số nêu trên có đáp ứng Biên độ - Tần số trùng với phổ của thông tin hữu ích. Trong [21], CuiWei Li đã đạt được kết quả như sau: Với việc sử dụng thang nhị thức

s  2k

với

k  1, 2,, mối quan hệ giữa k với đáp ứng Biên độ - Tần số

của bộ lọc được xác định gián tiếp qua công thức sau:











Qk ()  







k 1

G() G(2 )H( )

k 2

k  1 k  2 , k  2

trong đó:

G(2

)H(2 ) H( )

Qk () : Hàm biểu diễn đáp ứng tần số của bộ lọc thực hiện phép biến

đổi sóng nhỏ sử dụng thang

s  2k . Đáp ứng Biên độ - Tần số của bộ lọc

được phản ánh qua

Qk () .

i

G()  4ie 2

sin 2 , (3.10)

i3

H ()  e 2cos 2

. (3.11)

Với đột biến có dạng như sóng R của tín hiệu điện tim, có tốc độ biến đổi nhanh nhất so với các sóng còn lại (xem hình 1.1), sóng R có phổ phân bố

ở vùng tần số cao. Đáp ứng tần số Qk ()

được xác định dựa vào công thức

(3.9) cho thấy rằng tại

k  1, đáp ứng Biên độ - Tần số của Q1()

cũng có

phân bố tập trung tại vùng tần số cao, trùng với phân bố phổ của sóng R. Do

vậy

s  21

được chọn để giải bài toán tìm toạ độ đỉnh sóng R trên dãy tín

hiệu điện tim [21]. Theo CuiWei Li và các đồng sự, khi k  1, Q1()

có thể

được thay thế tương đương bởi Q1()

với:

trong đó

Q1() 

1 (1  ei ) .

2

Q1()

là đáp ứng tần số của bộ lọc số thực hiện phép biến đổi sóng nhỏ

W 1f (s, ) tại thang s  21 (xem công thức 1.20).

Q1()

là đáp ứng tần số tương đương của Q1() .

Hình 3.8 minh hoạ cho sự sai khác giữa

Q1()

và Q1() .

Hình 3.8: So sánh Đáp ứng Biên độ - Tần số của Q1()

và Q1() .

Trong đó: hình (a) phản ánh

Q1()

là Đáp ứng Biên độ - Tần số của Q1() .

Hình (b) phản ánh

Q1()

là Đáp ứng Biên độ - Tần số của Q1() . Hình (c)

phản ánh sai số tương ứng. Theo đó, sai số lớn nhất là: 1.33  1015 .

Đáp ứng xung tương ứng trong miền thời gian rời rạc hay là biến n là:

h1(n) 

1 ((n)  ( n 1)) . (3.12)

2

Với mục đích nâng cao độ chính xác cho bài toán dò tần số của nhiễu, chúng tôi cần đánh dấu các đột biến có khả năng gây nhầm lẫn do có dạng

gần giống với đột biến mang thông tin về

0 . Do điểm đột biến cần đánh dấu

nêu trên có đặc điểm là có tốc độ biến đổi chậm hơn đột biến tại 0

(xem

hình 3.5). Dạng đột biến này có phổ trong hình 3.9, trong đó phổ có thông tin tập trung chủ yếu tại 0    0.75 . Do vậy chúng tôi đề xuất sử dụng

thang s  22

cho việc thực hiện biến đổi sóng nhỏ để giải quyết yêu cầu đánh

dấu các đột biến không mang thông tin hữu ích nhưng có dạng gần giống với

đột biến cần quan tâm. Khi chọn thang s  22 , phổ

Q2()

của đáp ứng tần

số Q2()

được biểu diễn trong hình 3.10(a), qua đó ta thấy rằng

Q2()

lớn

nhất lân cận xung quanh tần số

  0.75 . Do vậy chọn thang s  22

sẽ tốt

hơn thang s  21 trong việc xác định các đột biến không mang thông tin.

Hình 3.9: Phổ của đột biến không mang thông tin..

Mặt khác, điểm qua không trên kết quả phép biến đổi sóng nhỏ bậc 1

W 1f (s, )

sẽ bị trễ so với toạ độ điểm 0

là 1  2k1 

điểm (xem [21]).

Do vậy, sử dụng thang s  22

để thực hiện biến đổi sóng nhỏ sẽ không phản

ánh chính xác toạ độ của 0 . Với mục đích xác định các đột biến không mang

thông tin, Q2()

được sử dụng vì có đáp ứng Biên độ - Tần số

Q2()

tập

trung tại tần số thấp hơn so với

Q1()

(xem hình 3.10).

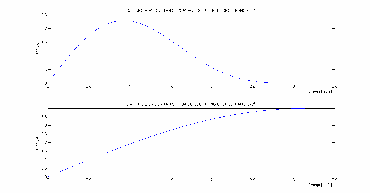
Hình 3.10: So sánh Đáp ứng Biên độ - Tần số của Q2() và Q1() .

Do đó sử dụng thang s  22

sẽ giúp phản ánh rõ hơn thông tin về điểm đột

biến có dạng gần giống điểm đột biến mang thông tin về 0 . Ta có thể thấy rõ hơn khi qua sát trên hình 3.11.

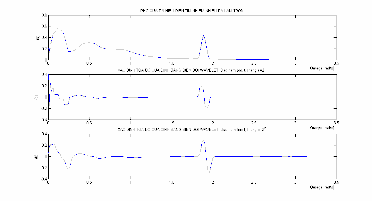
Hình 3.11:So sánh kết quả phép biến đổi sóng nhỏ dùng các thangs  21 và

s  22 .

sau:

Bộ lọc tương đương trong trường hợp

s  22

có đáp ứng tần số như

Q2()  0.256e3i 

 0.6e2i 

 0.28ei  0.28  0.6ei

 0.256e2i  ,

trong đó Q2()

là đáp ứng tần số của bộ lọc số tương đương dùng để thực

hiện phép biến đổi sóng nhỏ W 1f (s, ) sử dụng thang s  22 (xem công thức

1.20). Qua hình 3.12 ta thấy rằng sai số lớn nhất giữa

1.77  1015 .

Q2()

và Q2()

là:

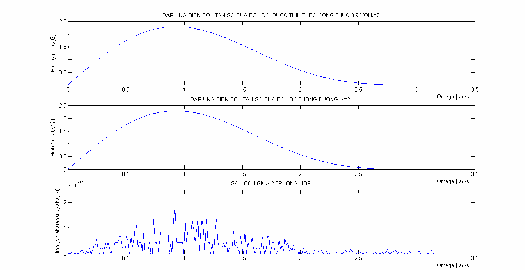
Hình 3.12:So sánh kết quả phép biến đổi sóng nhỏ dùng các thangs  21 và

s  22 .

Đáp ứng xung tương ứng trong miền thời gian rời rạc hay biến n là:

h2(n)  0.256(n  3)  0.6 ( n 2)  0.28 ( n 1)

(3.13)

 0.28(n)  0.6(n 1)  0.256 ( n 2)

Tương tự, sử dụng thang

s  21

cho việc tính W 2f (s, ) , được thực

hiện thông qua bộ lọc có đáp ứng tần số như sau:

U1()=g 1e2i  + g 2ei

với W 2f (s, ) : Phép biến đổi sóng nhỏ trên

g 3 + g 4ei  , (3.14)

f () , với thang s .

g1  g4 : Các hệ số của bộ lọc thực hiện phép biến đổi sóng nhỏ, với

g1= 0.4829629131 . g2  -0.8365163037 .

g3  0.2241438680 . g4  0.1294095226 .

Như đã trình bày ở trên, để lấy thông tin về phổ của tín hiệu, chỉ cần

biểu diễn

NoisyECG()

trong quãng

  0   . Khi đó ta có thể coi

Noi syECG()

là hàm số với biến  , và có đột biến tại

0 . Với mục đích

chuẩn bị cho việc sử dụng các kỹ thuật tính toán với biến rời rạc để xác định

toạ độ điểm đột biến ở các phần trình bày sau, chúng tôi đã rời rạc hoá đoạn

0  

của  . Khi đó, nếu khoảng cách giữa các điểm rời rạc là

S , phổ của

tín hiệu điện tim nhiễm nhiễu là hàm rời rạc

NoisyECG(nS )

với n  Z ,

xác định tại những điểm là bội của

S . Tương tự như cách biểu diễn tín hiệu

trong miền thời gian rời rạc, phổ của tín hiệu điện tim nhiễm nhiễu được biểu

diễn thành

Noi syECG(n)

, do đó thủ tục tìm 0

được chuyển thành tìm n0

với yêu cầu:

0 n0s

là nhỏ nhất. Do vậy việc chọn độ lớn của S

quyết

định độ phân giải của phổ của tín hiệu và có ảnh hưởng đến độ chính xác của thủ tục xác định toạ độ của điểm đột biến. Vấn đề này sẽ được chúng tôi đề cập đến trong mục 3.4.1 của luận án.

Việc rời rạc hoá  tương đương với với việc đổi từ biến  sang biến

n , do đó cho phép sử dụng các kết quả của CuiWei Li trong các công thức (3.12), (3.13) và (3.14) để tìm toạ độ điểm đột biến trong phổ của tín hiệu điện tim nhiễm nhiễu.

3.3. Mô hình lọc nhiễu và thuật giải tìm tần số của nhiễu từ đường tải điện sử dụng biến đổi sóng nhỏ.

Từ tiếp cận coi bài toán lọc thích nghi tương đương với 2 bài toán có thể giải được thông qua công cụ biến đổi Fourier và biến đổi sóng nhỏ. Chúng tôi đề xuất mô hình lọc nhiễu để giải bài toán trên như sau:

NoisyECG n   S n   N n  1

1 (n)

Làm trễ

a1

b1

Làm trễ

0

0.97

1

Giải thuật tìm tần số

0 của nhiễu

Tính hệ số:

a1  1.97 cos 0

Tính hệ số:

b1  2 cos 0

Hình 3.13: Mô hình lọc nhiễu từ nguồn cung cấp điện.

Trong đó

NoisyECG (n ) : là tín hiệu ta thu được từ bệnh nhân, chính là tín hiệu

điện tim đã bị nhiễm nhiễu (dưới dạng số).

NoisyECG n S n N n,

với

S(n)

là tín hiệu điện tim chưa nhiễm nhiễu.

N (n) : Nhiễu cộng tính ảnh

hưởng lên tín hiệu S(n) .

(n) là tín hiệu sau lọc nhiễu.

Giải thuật tìm tần số 0 của nhiễu.

Input:

 Dãy NoisyECG (n) , có độ dài L  2m

với m  Z .

 Hàm thực hiện biến đổi nhanh về Fourier, hàm làm trơn, hàm thực hiện bộ lọc có đáp ứng tần số trong công thức (3.12), công thức (3.13) và công thức (3.14).

Output:

 Tần số 0 của nhiễu Method

1. Kiểm tra điều kiện dữ liệu đầu vào

2. Thực hiện biến đổi Fourier nhanh đối với dãy

NoisyEC6()

NoisyECG (n )

ta có

3. Tính NoisyEC6()

4. Làm trơn

NoisyEC6()

, ta được

f () .

5. Tính

W 1f (s

 21, )

thông qua sử dụng bộ lọc có đáp ứng tần số

1 ) .

Q (

6. Tính W 1f (s

2

 22, )

thông qua sử dụng bộ lọc có đáp ứng tần số

Q ()

7. Tính W 2f (s, ) .

8. Tìm các cặp điểm cực đại - điểm cực tiểu cục bộ liên tiếp trên

W 1f(21, ) và W 1f (22, ) . Với điều kiện đoạn hàm số phải đơn điệu

giảm giữa 2 điểm cực cục bộ này. Thuật toán không tìm được 0

không tìm được các cặp cực đại - cực tiểu liên tiếp.

nếu