Đánh Giá Độ Chính Xác Và Mức Độ Phức Tạp Tính Toán Của Giải Thuật Tìm Tần Số 0 Của Nhiễu.

9. Xác định điểm qua không thoả mãn: nằm giữa 2 điểm cực đại, cực tiểu

cục bộ liên tiếp. Thuật toán không tìm được 0

điểm qua không tại bước này.

nếu không tìm được

10. Hiệu chỉnh giảm 1 đối với toạ độ các điểm qua không vừa tìm được

trên W 1f (22, )

tại bước 9.

11. Xác định toạ độ điểm đột biến không mang thông tin : So sánh các

điểm qua không trên W 1f (22, ) , W 1f (21, )

toạ độ điểm đột biến không mang thông tin.

và trên W 2f (s, )

để tìm

12. Toạ độ của đột biến mang thông tin tần của nhiểu 0

qua không còn lại trên W 1f (21, ) .

Kết thúc.

là toạ độ điểm

3.4. Đánh giá độ chính xác và mức độ phức tạp tính toán của giải thuật tìm tần số 0 của nhiễu.

Trong xử lý tín hiệu, yêu cầu thời gian thực tương đương với yêu cầu giảm thiểu độ phức tạp tính toán. Để đạt độ chính xác cao, các thuật giải thường có yêu cầu lớn về số lượng các phép tính. Đó là lý do mà cho đến nay, thuật toán LMS vẫn được sử dụng vì đặc tính đơn giản về tính toán và độ ổn định tốt. Đồng thời thuật toán LMS cũng được cải tiến để từng bước nâng cao độ chính xác. Điều này được minh chứng qua các công bố gần đây trong [8], [10], [12], [18], [29], [33], và [39]. Đó là lý do của việc chúng tôi sẽ so sánh độ phức tạp tính toán của thuật giải sử dụng biến đổi sóng nhỏ với thuật toán LMS khi cả hai cùng được sử dụng cho bài toán lọc triệt tần. Độ chính xác sẽ được đánh giá trực tiếp.

3.4.1. Đánh giá độ chính xác

Độ chính xác của thuật toán đề xuất phụ thuộc chủ yếu vào độ chính xác của việc dò tần số của nhiễu 0 . Do vậy để đánh giá độ chính xác, chúng

tôi dùng phương pháp kết hợp giữa đánh giá qua thống kê kết quả thực nghiệm và đánh giá sai số qua các bước thực hiện thuật toán.

Khi thực hiện thuật toán, sai số có thể xuất hiện tại các bước:

 Phép biến đổi Fourier và phép làm trơn.

 Tính W 1f (21, ) , W 1f (22, ) và W 2f (21, ) .

Đồng thời, sai số xảy ra do sự lựa chọn độ phân giải thấp của quãng Nyquyst.

Do phép biến đổi Fourier là phép biến đổi tuyến tính, nên không làm lệch toạ độ của điểm đột biến. Tuy nhiên, làm trơn phổ của tín hiệu điện tim

nhiễm nhiễu

NoisyEC6()

dẫn đến thay đổi theo chiều hướng không mong

đợi của hình dạng của đột biến cần tìm. Điều này rút ngắn lại sự khác biệt giữa đột biến mang thông tin và đột biến không mang thông tin. Vấn đề này đã được giải quyết tại bước 11 của thuật toán. Đối với biến đổi sóng nhỏ sử dụng trong thuật toán đề xuất, việc thực hiện đều thông qua các bộ lọc tương đương, có sai số. Sai số đã được xác định là lệch phải so với toạ độ thực của

0 và được tính như sau

Số điểm lệch phải = 1  2k1 ,

trong đó k

 Z 

là số mũ của thang 2k .

Do vậy, khi thực hiện thuật toán, các phép tính W 1f (21, ) và W 1f(22, )

không tạo ra sai lệch. Phép tính W 2f (21, )

tại bước 7 sẽ tạo ra sai lệch tại

bước 9, nhưng sai lệch đã được sửa lại tại bước 10.

Sai số do độ phân giải thấp của quãng Nyquyst được giải thích như sau: Vì biến đổi Fourier được coi là phép xấp xỉ 1 hàm bất kỳ thành tổng của các hàm sin , cos , và như đã giải thích trong 3.2.1, ta chỉ cần quan sát đáp ứng Biên độ tần số trên quãng Nyquyst, từ 0 đến  . Phổ của tín hiệu được thực hiện qua phép biến đổi Fourier, như đã trình bày ở 3.2.3, sau đó quãng Nyquyst được chia thành các đoạn rời rạc, thường là 511 đoạn. Do vậy, độ

lớn của sai số sẽ tỷ lệ nghịch với độ phân giải của quãng Nyquyst. Trong trường hợp này, sai số tương tự như sai số khi lượng tử hoá của việc rời rạc hoá tín hiệu. Đây là sai số không thể tránh khỏi, nếu ta giảm thiểu sai số bằng cách tăng độ phân giải trong không gian tần số  , độ phức tạp tính toán của phép biến đổi sóng nhỏ sẽ tăng lên đáng kể. Mối quan hệ giữa độ phân giải trong không gian tần số với độ chính xác và độ phức tạp tính toán được liệt kê

trong bảng (3.1). Chúng tôi lựa chọn giải pháp chia quãng 0   thành 255

đoạn rời rạc không những đủ đáp ứng yêu cầu độ chính xác cho việc xác định

0 mà còn tạo cho thuật toán có độ phức tạp tính toán đủ tốt.

Chúng tôi nhận thấy rằng trong mọi mức độ phân giải, sai số lớn nhất

luôn tập trung xung quanh tần số   1.5708 rad / s  2.0818 rad / s . Điều

này gợi ý cho một tiếp cận khác để giải quyết vấn đề giảm thiểu sai số nhưng không làm tăng độ phức tạp tính toán. Đó là dùng phân bố không đồng nhất,

mật độ cao sẽ tập trung xung quanh tần số

  1.5708 rad / s

và tại những

tần số có xác suất xuất hiện cao.

Ngoài các nguyên nhân gây sai số mang tính chủ quan như đã nêu trên,

nếu nhiễu có tần số 0

rơi vào trong dải 0 rad / s 0.1 rad / s và

0.2 rad / s 0.3 rad / s khi đó đột biến mang thông tin sẽ nằm liền kề với đột

biến không mang thông tin. Khi đó thuật toán không thể dò được tần số 0

của nhiễu. Tuy nhiên 2 dải tần số nêu trên nằm trong vùng tần số rất thấp, mạng điện cung cấp không bao giờ có tần số nằm trong khoảng này.

Các thực nghiệm nhằm đánh giá độ chính xác của thuật toán được cài đặt trên Matlab 6.5, chạy trên PC có cấu hình: Pentium 2x2GHz, RAM: 1GB. Các kết quả được tóm tắt trong bảng 3.1 dưới đây:

Bảng 3.1: Thống kê kết quả dò tìm tần số của nhiễu

0 .

TT

Dải tần của nhiễu rad / s	Số lượng thực nghiệm	Phát hiện sai		Không phát hiện được
		Số lượng	%	Số lượng	%
1	0  0.1	2000	16	8	1804	92
2	0.1 0.2	2000	0	0	10	0.5
3	0.2  0.3	2000	20	10	1800	90
4	0.3  0.4	2000	4	0.2	8	0.4
5	0.4  0.5	2000	0	0	6	0.3
6	0.5 1	1000	0	0	0	0
7	1.0 1.5	1000	0	0	0	0
8	1.5  2.5	1000	0	0	0	0
9	2.5  3.0	1000	0	0	0	0

Có thể bạn quan tâm!

•  Thay Đổi, Eeg Trước Và Sau Lọc Nhiễu, Đoạn N  2001  3000 .
• Kỹ Thuật Làm Nổi Bật Đặc Tính Của Nhiễu Bằng Biến Đổi Fourier.
• So Sánh Kết Quả Phép Biến Đổi Sóng Nhỏ Dùng Các Thangs  21 Và
• Kết Quả Ước Lượng Đạo Hàm Bậc I Dùng Biến Đổi Sóng Nhỏ S  21
• Các phương pháp thích nghi trong lọc nhiễu tín hiệu điện tim - 15
• Các phương pháp thích nghi trong lọc nhiễu tín hiệu điện tim - 16

Xem toàn bộ 130 trang tài liệu này.

3.4.2. Đánh giá mức độ phức tạp tính toán.

Phép biến đổi Fourier và biến đổi sóng nhỏ sử dụng trong thuật giải sử dụng biến đổi sóng nhỏ, có thể được thực hiện qua các biến đổi nhanh mà không làm sai lệch thông tin (xem [21], [23]).

Nếu gọi L là độ dài của một chu kỳ tín hiệu điện tim đã được rời rạc hoá thì số các phép tính để thực hiện biến đổi Fourier nhanh được biểu diễn qua công thức (3.15)

L log 2 2

L (3.15)

Theo S.Mallat trong [23], nếu ta thực hiện biến đổi sóng nhỏ thang

s  2k

để xác định toạ độ điểm đột biến trên dãy có độ dài N thì số các phép

toán cần thực hiện được mô tả trong công thức (3.16)

N log2 N (3.16)

Tín hiệu điện tim được thu nhận với dải tần số từ 0.1 Hz đến 80Hz

(xem [3]), Do vậy tần số lấy mẫu được chọn fs  166Hz . Để thu nhận đầy đủ

thông tin về phổ của tín hiệu, cần thu nhận ít nhất 1 chu kỳ nhịp tim. Ở trạng thái nghỉ, tim người đập chậm nhất là 40 nhịp/ phút. Do vậy chỉ cần tối đa thời gian 1.5 giây cho việc thu nhận tín hiệu từ bệnh nhân. Với tần số lấy mẫu

fs  166Hz

và thời gian tối thiểu để thu nhận tín hiệu là 1.5 giây, dãy tín

hiệu thu nhận có độ dài tối thiểu là L  249 . Do vậy chúng tôi chọn

L  256 . Độ dài này, sẽ thoả mãn yêu cầu cần thiết để phép biến đổi Fourier cho kết quả phản ánh đầy đủ thông tin của tín hiệu. Vì ta chia không gian tần số thành 255 đoạn, nên N  256. Từ công thức (3.15) số phép tính cần thiết để thực hiện phép biến đổi FFT là 1024 . Từ công thức (3.16), số phép tính cần thiết để thực hiện biến đổi sóng nhỏ là 2048 phép tính. Trong thuật toán đề xuất, chúng tôi dùng 3 phép biến đổi sóng nhỏ, do vậy tổng số phép tính để thực hiện các biến đổi sóng nhỏ là 6144 phép tính.

Với các kết quả được công bố gần đây nhất, thuật toán LMS với kích thước bước thích nghi thay đổi hội tụ nhanh nhất sau ít nhất 500 vòng lặp, do vậy với thuật toán được công bố trong [29] số lượng các phép tính cần thiết cho thuật toán LMS hội tụ là: 7500 phép tính. Như vậy độ phức tạp tính toán của 2 phương pháp là tương đương. Tuy nhiên, trên thực tế, thời gian thu nhận tín hiệu nhỏ hơn rất nhiều, kết hợp với giảm bớt độ phân giải của không gian tần số nên số lượng phép tính sẽ giảm đáng kể. Bảng 3.2 mô tả mối quan hệ giữa độ phân giải của không gian tần số với số phép tính của mỗi lần biến đổi sóng nhỏ và sai số có thể xảy ra.

Bảng 3.2. Mối quan hệ giữa độ phân giải trong không gian tần số với sai số tính toán và độ phức tạp tính toán.

TT

Độ phân giải của không gian tần số	Sai số lớn nhất có thể gặp	Sai số trung bình	Số phép tính cần thiết để thực hiện WT
1	63	0.0499	0.0317	384
2	127	0.0247	0.0157	896
3	255	0.0123	0.0078	2048
4	511	0.0061	0.0039	4608
5	1023	0.0031	0.0020	10240
6	2047	0.0015	0.00097	22528
7	4095	0.00076718	0.00048840	49152
8	8191	0.00038354	0.00024417	106496
9	16383	0.00019176	0.00012208	229376
10	32767	0.000095877	0.000061037	491520
11	65535	0.000047938	0.000030518	1048576
12	131071	0.000023969	0.000015259	2228224

3.5. Thực nghiệm và kết quả

Để so sánh mô hình lọc nhiễu và thuật toán dò tần số đề xuất ở chương này với các mô hình và thuật toán lọc nhiễu thích nghi mới nhất, chúng tôi sử dụng công thức 2.7 để tính trung bình của bình phương sai số (MSE). Tốc độ hội tụ được đánh giá qua tốc độ giảm về gần 0 của MSE. Độ ổn định được phản ánh qua độ dao động của MSE.

Thực nghiệm 3.1:

Đối với tín hiệu điện tim: Để có thể đánh giá độ chính xác của mô hình và giải thuật đề xuất và đánh giá sai số trung bình bình phương, chúng tôi sử

dụng tín hiệu điện tim thật đã được rời rạc hoá như là tín hiệu điện tim sạch,

được ký hiệu là S(n) trên mô hình lọc nhiễu đề xuất (Hình 3.13). Trong miền

thời gian, tín hiệu

S(n)

được biểu diễn trong hình 3.14(a). Theo các tác giả

trong [13] và [44], với bài toán lọc nhiễu từ đường tải điện, tín hiệu nhiễu có thể được mô phỏng theo công thức 2.9. Trên mô hình đề xuất (Hình 3.13),

nhiễu này ký hiệu là N (n) và được minh hoạ trên hình 3.14 (b). Tín hiệu điện

tim nhiễm nhiễu là tổng của S(n)

và N (n) , được ký hiệu là

NoisyECG (n ) .

Hình 3.14(c) biểu diễn NoisyECG(n) trong miền thời gian.

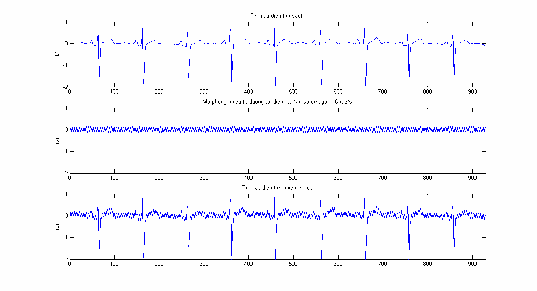
Hình 3.14: Biểu diễn trong miền thời gian các tín hiệu S(n) , N (n) và

NoisyECG (n)

Chúng tôi sử dụng giải thuật đề xuất để tìm tần số của nhiễu, các bước chính

được minh hoạ như sau:

Thực hiện biến đổi Fourier nhanh đối với tín hiệu NoisyECG (n ) , kết

quả được biểu diễn trong hình 3.15(a). Kết quả phép làm trơn được biểu diễn trong hình 3.15(b). Kết quả của việc sử dụng biến đổi sóng nhỏ tại thang

s  21

để ước tính đạo hàm bậc I đối với phổ đã được làm trơn của

NoisyECG (n) , được biểu diễn trên hình 3.15(c). Tương tự, hình 3.15(d) là kết quả phép biến đổi sóng nhỏ với thang s  22 . Hình 3.15(e) là kết quả của phép tính đạo hàm bậc II sử dụng biến đổi sóng nhỏ tại thang s  21 .

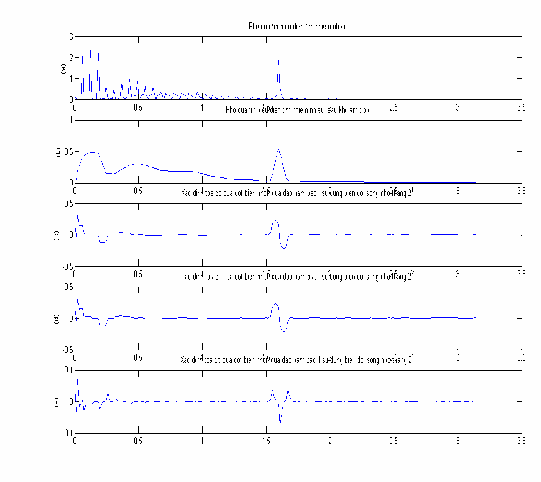
Hình 3.15: Các kết quả chính khi thực hiện giải thuật tìm tần số của nhiễu

Toạ điểm đột biến được xác định tại 0

 1.6 rad / s . Để thuận lợi cho

việc quan sát kết quả, hình 3.16 sẽ biểu diễn tập trung vào xung quanh tần số của nhiễu.