Đường Sức Của Điện Trường Gây Ra Bởi Điện Tích Điểm

*

đó, d Et

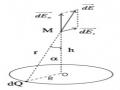
do dQ* gây ra đối xứng với d Et qua trục OM, cặp điện trường này

đôi một triệt tiêu nên tổng các thành phần d Et trên toàn dây dẫn bằng không. Còn lại:



EM d En vòng

Vì các vector d En cùng phương, chiều nên E M có điểm đặt tại M, có phương của trục vòng dây và chiều hướng ra xa vòng dây. Về độ lớn thì:

Có thể bạn quan tâm!

Xem toàn bộ 258 trang tài liệu này.

EM 

vòng

dEn

Bước 4: Tìm các đại lượng có liên quan và giải. Để tìm được lời giải cho bài toán tích phân, cần chuyển tất cả các biến số về một biến duy nhất.

Theo hình vẽ ta có gây bởi dQ tại M bằng:

dEn dE cos

(là góc giữa d Evà OM ). Điện trường

dE k dQ

r2

Vì: cosh ,

r2 R2 h2

nên:

dEn

k hdQ

r3

k hdQ



3

(R2 h2 ) 2

hQ 3

Vậy:

EM 



vòng

dEn k 

(R2 h2 )

2 dQ

vòng

Nhận xét:

EM k

hQ (R2 h2 )2



 Tại tâm vòng dây: h  0, do đó E0  0

 Ở nơi khá xa vòng dây: h  R, r h, EM

kQ

h2

 Nếu vòng dây tích điện âm ( Q  0 ) thì EM có chiều hướng vào tâm O của vòng dây và có độ lớn.

EM k

hQ (R2 h2 )2



1.4. ĐIỆN THÔNG

1.4.1. Đường sức điện trường

a. Định nghĩa

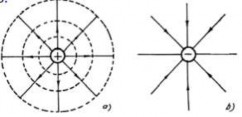
Đường sức điện trường là đường cong mà tiếp tuyến tại mỗi điểm của nó trùng với phương của vectơ cường độ điện trường tại điểm đó, chiều của đường sức điện trường là chiều của vectơ cường độ điện trường.

Như vậy, đường sức của một điện trường đều là những đường thẳng song song, đường sức của điện trường gây ra bởi điện tích điểm là những đường thẳng hướng vào điện tích điểm nếu là điện tích âm và hướng

ra xa khỏi điện tích điểm nếu là điện tích dương.

b. Quy ước

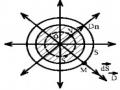
Hình 1.4. Đường sức điện trường

Hình 1.5. Đường sức của điện trường gây ra bởi điện tích điểm

Số đường sức điện trường qua một đơn vị diện tích đặt vuông góc với đường sức tỉ lệ với cường độ điện trường E tại nơi đặt diện tích đó. Tập hơp̣

các đường sứ c đi ện trường đươc phổ.

goi

là phổ đường sứ c đi ện trư ờng hay đi ện

Số đường sức điện

~ E

Diện tích 

(1.14)

Từ qui ước trên , qua điện phổ nếu chỗ nào m ật độ đường sứ c lớn (dày)

thì nơi đó điện trường maṇ h, còn nơi nào mật độ đường sứ c nhỏ (thưa) thì nơi ấy điện trường yếu. Với điện trường đều ( E const ) điện phổ là những đường thẳng song song cách đều nhau.

Nhận xét

 Đường sứ c đi ện trường xuất phát từ đi ện tính dương , tận cùng trên điện tích âm.

 Đường sứ c của điện trường tinh là những đường cong hở.

 Các đường sứ c đi ện trường không cắt nhau vì taị mỗi điểm trong điện trường véctơ E chỉ có một hướng xác điṇ h.

1.4.2. Sư ̣ gián đoan

củ a đường sứ c điện trường - Vectơ cảm ứng điện

Từ biểu thức cường độ điện trường E cho thấy ở trong môi trường, cường độ điện trường giảm đi lần so với trong chân không.

Như vậy, khi đi qua mặt ngăn cách giữa chân không và môi trường, phổ đường sức sẽ bị gián đoạn tại mặt phân cách.

Để thuận tiện cho việc tính toán, người ta khử sự gián đoạn đó bằng cách đưa vào một đại lượng gọi là vectơ cảm ứng điện D được định nghĩa:

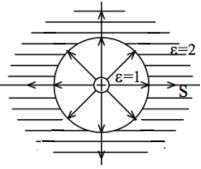
Hình 1.6. Sự gián đoạn của đường sức điện trường

D 0 E (1.15)

Vậy vectơ cảm ứng điện do điện tích điểm q gây ra tại một điểm M cách

q một khoảng r là:



D (1.16)

4r2 r

D  (C m2 ) (1.17)

4r2

Tại mỗi điểm trong điện trường, D chỉ phụ thuộc vào nguồn sinh ra điện trường mà không phụ thuộc vào tính chất của môi trường.

Khái niệm đường sức được đưa ra tương ứng với đại lượng vectơ cường độ điện trường, tương tự, người ta đưa ra khái niệm đường cảm ứng điện tương ứng với vectơ cảm ứng điện như sau:

Đường cảm ứng điện là đường cong mà tiếp tuyến tại mỗi điểm của nó trùng với phương của vectơ cảm ứng điện, chiều là chiều của vectơ cảm ứng điện. Số đường cảm ứng điện qua một đơn vị diện tích đặt vuông góc tỉ lệ với độ lớn

vectơ cảm ứng điện tại nơi đặt diện tích đang xét.

Số đường cảm ứng

~ D

Diện tích 

(1.18)

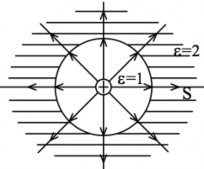
Hình 1.7. Sự liên tục của các đường cảm ứng điện

Như vậy, khi đi qua mặt phân cách giữa hai môi trường có hằng số điện môi khác nhau, các đường cảm ứng điện liên tục còn các đường sức bị gián đoạn.

1.4.3. Điện thông

a. Định nghĩa

Điện thông gửi qua diện tích S là một đại lượng có trị số tỷ lệ với số đường cảm ứng điện cắt diện tích đó.

b. Biểu thức

Trước hết ta xét điện thông của một điện trường đều gửi qua một tiết diện phẳng.

Nhận xét:số đường cảm ứng điện cắt một tiết diện phẳng S bất kì đặt trong điện trường D chính bằng số đường cảm ứng điện

28 Hình 1.8. Điện thông của điện

trường đều gửi qua tiết diện phẳng

cắt Sn là hình chiếu của S trên mặt phẳng vuông góc với D .

Gọi n là vectơ pháp tuyến của tiết diện S, n hợp với D một góc . Ta có: Sn S. cos .

Kí hiệu: S S.n gọi là vectơ diện tích S.

Từ định nghĩa của điện thông và quy ước (1.18) ta có: điện thông gửi qua diện tích S chính bằng điện thông gửi qua Sn và bằng:

e D.Sn D.S. cosDn.S D.S (1.19)

Chú ý:

 0

 0

 0

Xét điện thông của một điện trường bất kỳ gửi qua một tiết diện có hình dạng tùy ý.

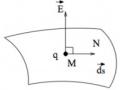
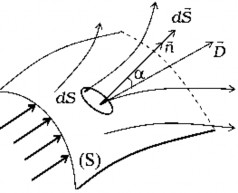
Hình 1.9. Điện thông gửi qua diện tích dS

Khi đó, dễ dàng chuyển về trường hợp điện trường đều và tiết diện phẳng bằng cách chia mặt S thành vô số các phần tử diện tích dS vô cùng nhỏ sao qua mỗi phần tử dS có thể coi là phẳng và điện trường gửi qua dS là đều.

Điện thông de của D gửi qua dS là:

de D.dS D.dS. cos(D, dS) (1.20) Điện thông gửi qua toàn bộ diện tích S là:

e de D.dS Dn. dS

(1.21)

Chú ý

(S )

Đối với mặt kín, ta luôn chọn chiều của pháp tuyến n là chiều hướng ra phía ngoài của mặt kín đó.

 Nếu D hướng ra phía ngoài mặt kín e  0 (ví dụ điện thông gửi qua mặt cầu bao quanh điện tích dương nhận giá trị dương).

 Nếu D hướng vào trong mặt kín e  0 (ví dụ điện thông gửi qua mặt cầu bao quanh điện tích âm nhận giá trị âm).

1.5. ĐỊNH LÝ OXTROGRATXKI - GAUSS (O - G) ĐỐI VỚI ĐIỆN TRƯỜNG

1.5.1. Thiết lập định lý

Tính điện thông của điện tích điểm gửi qua mặt kín trong các trường hợp

Mặt kín S0 là mặt cầu bao quanh điện tích điểm có tâm trùng với điện tích điểm

e (S0 ) 



(S0 )

D.dS



trong đó: D 

4r2 r

  r

Hình 1.10. Điện thông qua mặt kín S0

dS dS.n dS.

Nhận xét:tại mọi điểm trên mặt cầu D có độ lớn như nhau và hướng theo bán kính của mặt cầu, nghĩa là D cùng chiều dS. Vậy:

(S ) 

dS q ( r )2 

dS q q

dS q

4r2

e 0

(S0 )

4r2 r

(S0 )

4r2

(S0 )

4r2

Nhận xét:

e (S0 ) q. (1.22)

 Điện thông do điện tích điểm gửi qua mặt cầu không phụ thuộc vào bán kính của mặt cầu.

 Có q đường cảm ứng điện đi ra khỏi mặt cầu từ một điện tích điểm dương và ngược lại có q đường cảm ứng điện đi vào mặt cầu từ một điện tích âm.

Mặt kín là một mặt bất kì bao quanh điện tích điểm

Xét mặt kín S1 là mặt bất kì bao quanh điện tích q trong đó các đường cảm ứng điện chỉ cắt S1 một lần.

Hình 1.11

Do đường cảm ứng điện là liên tục ngay cả tại mặt phân cách giữa hai môi trường khác nhau nên có bao nhiêu đường cảm ứng điện cắt S0 thì cũng có bấy nhiêu đường cảm ứng điện cắt S1.

Theo định nghĩa, điện thông tỉ lệ với số đường cảm ứng điện, do đó, điện thông gửi qua hai diện tích S0 và S1 là bằng nhau.

(S ) (S ) q.

e 0 e 1

Xét mặt kín S2 là mặt bất kì bao quanh điện tích q. Khi đó các đường cảm ứng điện chỉ có thể cắt S2 một số lẻ lần.

Xét trường hợp đường cảm ứng điện cắt S2 3 lần (và q  0), ta có:

 Lần 1, đường cảm ứng điện đi ra khỏi mặt kín e 1,

 Lần 2, đường cảm ứng điện đi vào trong mặt kín e 1,

 Lần 3, đường cảm ứng điện đi ra khỏi mặt kín e 1.

Như vậy, dù đường cảm ứng điện cắt mặt kín một số lẻ lần thì nó cũng chỉ có tác dụng về mặt điện thông tương đương với đường cảm ứng điện cắt mặt kín một lần. Nghĩa là điện thông gửi qua S1 và S2 là như nhau:

e (S0 ) e (S1 ) e (S2 ) q.

Mặt kín S3 không bao quanh điện tích (điện tích nằm ngoài mặt kín)

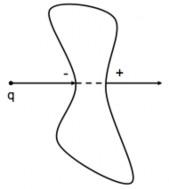
Nếu các điện tích không nằm trong mặt kín thì điện thông gửi qua mặt kín đó bằng không vì số đường cảm ứng đi vào bằng số đường cảm ứng đi ra khỏi mặt kín đó.

Kết luận

e (S3 )  0

 Điện thông do một điện tích gây ra gửi qua mặt kín có giá trị bằng q nếu q nằm trong mặt kín và bằng không nếu q nằm ngoài mặt kín.

 Điện thông không phụ thuộc vào vị trí đặt điện tích ở trong mặt kín và không phụ thuộc vào cách chọn hình dạng mặt kín.

Hình 1.12

 Trường hợp có nhiều điện tích, điện thông gửi qua mặt kín bằng tổng điện thông do từng điện tích gây ra cho mặt kín đó.

1.5.2. Phát biểu định lý

Điện thông gửi qua một mặt kín bằng tổng đại số các điện tích chứa trong mặt kín đó:

e(S) D.dS qi

(1.23)

(S ) i

1.5.3. Dạng vi phân của định lý O-G

Theo giải tích vectơ:



DivD 

dDx dx

dDy

dDz

  OG

DdS divD. dV qi

(S ) (V ) i

Trong trường hợp điện tích phân bố liên tục với mật độ khối , ta có: