Cường Độ Điện Trường Gây Ra Bởi Một Điện Tích Điểm

   q Q  q Q 

2

F = F + F = k1r +k2r

1

1 2 r3 1

r32

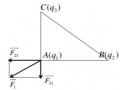
Điều kiện để Q đứng yên (cân bằng) là:

F = 0

Có thể bạn quan tâm!

• Vật lý đại cương 2 - 1
• Vật lý đại cương 2 - 2
• Đường Sức Của Điện Trường Gây Ra Bởi Điện Tích Điểm
• Thế Năng Của Điện Tích Trong Điện Trường
• Liên Hệ Giữa Vectơ Cường Độ Điện Trường Và Hiệu Điện Thế

Xem toàn bộ 258 trang tài liệu này.

q Q  q Q 

hay: k1r k2r

1

2

r3 1 r3 2

Ta thấy vì q1 và q2 cùng dấu nên r1 và r2 phải ngược chiều nhau (với mọi Q ), nghĩa là điện tích điểm Q phải đặt tại điểm M nằm trên đoạn thẳng nối q1 và q2 và nằm ở giữa hai điện tích ấy.

 Nếu

 Nếu

Q  0 : nó cùng bị q1 và q2 đẩy.

Q  0 : nó cùng bị q1 và q2 hút.

Từ điều kiện cân bằng ta có:

1

2

k q1Q k q2Q

r2 r2

Suy ra:

q2

q1

r2 q r

9

222

 3

r

q

r

2

1 1 1

Mặt khác:

r1 r2 a

r a và r 3a

Kết luận:

1 4 2 4

 Điện tích Q có thể âm, dương và có độ lớn tùy ý.

 Nếu Q  0 : Khi lệch khỏi M, hợp lực kéo nó trở lại (trạng thái cân bằng bền).

 Nếu Q  0 : Khi lệch khỏi M, hợp lực đẩy nó đi tiếp (trạng thái cân bằng không bền).

1.3. ĐIỆN TRƯỜ NG

1.3.1. Khái niệm điện trường

Theo định luật Coulomb, các điện tích tương tác tĩnh điện với nhau ngay cả khi chúng đặt cách nhau một khoảng r nào đó trong chân không. Vậy chúng ta phải lí giải sự xuất hiện của lực tĩnh điện như thế nào khi các điện tích không hề tiếp xúc nhau, và giữa chúng không có chất truyền tương tác?

Để trả lời cho câu hỏi trên, trong tiến trình phát triển của vật lý học, các nhà khoa học đã đưa ra hai thuyết đối lập nhau: thuyết tương tác gần và thuyết tương tác xa.

Theo thuyết tương tác gần, để giải thích sự xuất hiện của lực tĩnh điện người ta đưa vào khái niệm điện trường. Điện trường là một dạng đặc biệt của vật chất bao quanh các điện tích. Khi đặt một điện tích vào trong không gian thì không gian bao quanh điện tích tồn tại một điện trường, và điện trường này sẽ tác dụng lực điện lên các điện tích khác đặt trong nó.

Khoa học hiện đại đã xác nhận sự đúng đắn của thuyết tương tác gần và sự tồn tại của điện trường.

Sự tồn tại của điện trường cũng tương tự với sự tồn tại của trường hấp dẫn. Trường hấp dẫn giải thích lực tương tác (hút) giữa hai vật có khối lượng đặt cách nhau trong không gian, còn điện trường giải thích sự xuất hiện của lực tĩnh điện (hút hoặc đẩy) giữa hai điện tích.

1.3.2. Vectơ cường độ điện trường

a. Định nghĩa

Để đặc trưng cho điện trường về phương diện tác dụng lực lên điện tích đặt trong nó, người ta đưa ra khái niệm vectơ cường độ điện trường.

Vectơ cường độ điện trường do một điện tích điểm q0 gây ra tại một điểm M trong không gian sẽ đặc trưng cho khả năng tác dụng lực (mạnh hay yếu) của điện trường lên một điện tích đặt tại M. Do đó, vectơ cường độ điện trường phụ thuộc vào điện tích sinh ra điện trường, và phụ thuộc vào vị trí cần xác định cường độ điện trường M nhưng không phụ thuộc vào điện tích thử tại M.

Tại m ột điểm M trong điện trường của điện tích q0 ta lần lươt

đặt các

điện tích q1, q2, ..., qn có giá tri ̣đủ nhỏ (để không làm biến đổi đáng kể đi ện

trường đó ) rồi đo các lưc

F1, F2, ..., Fn do điện trường tác dun

g lần lươt

lên

chúng. Thưc

nghiệm cho thấy tỉ số giữa lưc

tác dụng lên mỗi đi ện tích và tri

đaị số của điện tích đó là một hằng số:

const

F1F2 ... Fn

(1.6)

q1 q2 qn

Vectơ hằng số này đ ặc trưng cho đi ện trường taị điểm M cả về đ ộ lớn,

phương và chiều; nó đươc hiệu là E :

goi

là vectơ cường độ điện trường taị điểm M, kí

F



E (1.7)

q

trong đó, E là vectơ cường độ điện trường do điện tích điểm q0 sinh ra tại M,

F là lực do điện trường của q0 tác dụng lên điện tích thử q đặt tại M.

Từ biểu thứ c (1.7) ta thấy nếu chon q  1 thì E F . Vậy:

“Vectơ cường độ điện trường E tại một điểm là đaị lương đ ặc trưng cho

điện trường taị điểm đó về phương di ện tác dun

g lưc

, có tri ̣vectơ bằng lực tác

dụng của điện trường lên một đơn vi ̣điện tích dương đặt taị điểm đó.”

Trong hệ đơn vi ̣SI, cường độ điện trường có đơn vi ̣đo là Vôn/mét (V/m).

Lưc

điện trường tác dun

g lên điện tích điểm

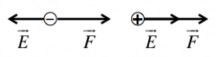
Lực tác dụng lên điện tích điểm q đặt tại

M có cường độ điện trường E là:

F qE (1.8)

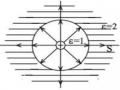
 Nếu q  0 thì F ngược chiều với E (Hình 1.2);

 Nếu q  0 thì F cùng chiều với E (Hình 1.2).

Hình 1.2

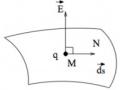
b. Vectơ cường độ điện trường gây ra bởi điện tích điểm

Xét một điện tích điểm có tri ̣đaị số q . Trong không gian bao quanh nó

sẽ xuất hi ện điện trường . Ta hãy xác điṇ h véctơ cường đ ộ điện trường E tại một điểm M cách điện tích q một khoảng r. Muốn vậy taị điểm M ta đặt một điện tích điểm q0 có tri ̣số đủ nhỏ (để không làm biến đổi điện trường q ). Khi

đó theo điṇ h luật Coulomb, lưc

tác dụng của điện tích q lên điện tích q0 bằng:

1

F 

 q.q0r

(1.9)

2

40 r r

So sánh vớ i biểu thứ c điṇ h nghia (1.7), ta thấy véctơ cường đ ộ điện

trường do điện tích điểm q gây ra taị điểm M là:

F

 1

q

r



E (1.10)

q0 40 r r

2

trong đó bán kính véctơ r hướng từ điện tích q đến điểm M.

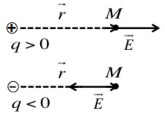
Nhận xét:

 Nếu q  0 thì E ↗↗ r : E hướng ra xa khỏi điện tích q .

 Nếu q  0 thì E ↗↙ r : E hướng

vào điện tích q .

 Về độ lớn:

1 q

2

E 

40 r

Hình 1.3. Cường độ điện trường gây ra bởi một điện tích điểm

(1.11)

c. Vectơ cường độ điện trường gây ra bởi một hệ vật mang điện - Nguyên lý

chồng chất điện trư ờng

Cường độ điện trư ờng gây ra bởi hệ điện tích điểm phân bố rời rac̣

Xét hệ điện tích điểm q1, q2, ..., qn đươc

phân bố rời rac

trong không

gian. Để xác điṇ h véctơ cường đ ộ điện trường tổng hơp

E tại m ột điểm M

nào đó của không gian , ta đặt tai M một điện tích q0 . Khi đó theo (1.5) lưc

tổng hơp

tác dun

g lên điện tích q0 bằng:

 n

Fi là lưc

tác dun

F Fi

i1

g của điện tích qi lên điện tích q0 .

Vậy vectơ cường độ điện trường tổng hợp tại M là:

n

n

  Fi

E F

q0

i1

q0

Fi

i1 q0

(1.12)

 n

E Ei

i1

với Ei là vectơ cường độ điện trường do điện tích qi gây ra tại M.

Biểu thứ c (1.12) là biểu thứ c toán hoc của nguyên lý chồng chất đi ện

trường đươc

phát biểu như sau:

Véctơ cường đ ộ điện trường gây ra bởi m ột hệ điện tích điểm bằ ng tổng các véctơ cường độ điện trường gây ra bởi từ ng điện tích điểm của hệ.

Cường độ điện trư ờng gây bởi hệ điện tích điểm phân bố liên tuc̣

Xét một vật mang điện có kích thước bất kỳ và đi ện tích phân bố liên tuc̣

trên vật này. Rò ràng ta có thể xem v ật như một hệ điện tích điểm đươc

phân

bố liên tuc

trong không gian . Do đó để tính cường đ ộ điện trường gây bởi v ật

này ta tưởng tương chia v ật thành nhiêù phần nhỏ sao cho điện tích dq trên

mỗi phần đó có thể xem là điện tích điểm. Nếu goi

dE là véctơ cường độ điện

trường gây ra bởi đi ện tích dq tại điểm M cách dq một khoảng r thì véctơ

cường độ điện trường do vật mang điện gây ra taị điểm M đươc công thứ c:

xác điṇ h theo

  

1 dq r

2

(1.13)

Bài toán 3:

E d E 

toàn vât

toàn vât

40 r r

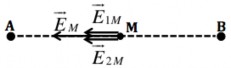
Có hai điện tích điểm q1

109 C; q

109 C đặt tại hai điểm A và B cách

2

nhau 3cm. Xác định vectơ cường độ điện trường tại trung điểm M của AB.

Giải:

Định hướng:

Đây là dạng bài toán tìm cường độ điện trường do một hệ điện tích điểm gây ra tại một điểm M nào đó. Do vậy, để giải bài toán ta cần áp dụng nguyên lí chồng chất điện trường áp dụng cho hệ điện tích điểm phân bố rời rạc, nghĩa là cần xác định được phương, chiều và độ lớn của từng vectơ cường độ điện trường thành phần sau đó tổng hợp vectơ theo quy tắc hình bình hành.

Bước 1: Xác định các điện tích gây ra điện trường tại M là: q1, q2. Các vectơ cường độ điện trường tại M là E1M , E2 M

Bước 2: Vẽ hình.

Chú ý xác định đúng điểm đặt vectơ cường độ điện trường (tại M), phương (AB) và chiều (lại gần điện tích âm q1, ra xa điện tích dương q2)

của các vectơ E1M , E2 M

Bước 3: Áp dụng nguyên lý chồng chất điện trường:

EM E1M E2 M

Bước 4: Cộng vectơ theo quy tắc hình bình hành.

Nhận xét: E1M & E2 M cùng phương, cùng chiều

EM E1M E2 M

1

q1

Bước 5: Tìm các đại lượng có liên quan (nhớ đổi đơn vị và nhớ lấy dấu trị tuyệt đối) và giải:

0

E1M

 4

AM 2

E2 M

 1

40

q2 BM 2

E1M E2 M  9.10

109 4

9 

104 9.10

(V m)

EM

 2E1M

 18.104 (V m)

(nếu xác định sai chiều của một trong hai vectơ cường độ điện trường hoặc quên lấy dấu trị tuyệt đối, cường độ điện trường tại M sẽ bị triệt tiêu)

Bài toán 4:

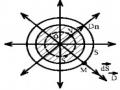
Một vòng tròn làm bằng một dây dẫn mảnh bán kính R mang điện tích dương Q phân bố đều trên dây. Hãy xác định cường độ điện trường tại điểm M nằm trên trục của vòng dây, cách tâm một đoạn h .

Giải:

Định hướng:

Đây là dạng bài toán tìm cường độ điện trường do một hệ điện tích phân bố liên tục (vật mang điện có kích thước đáng kể) gây ra tại một điểm M trong không gian. Để xác định vectơ cường độ điện trường ta chỉ có công cụ duy nhất là công thức xác định điện trường gây ra bởi một điện tích điểm, vì vậy cần chia vật mang điện thành các phần tử điện tích có kích thước vô cùng nhỏ dq (điện tích điểm) sau đó áp dụng nguyên lý chồng chất điện trường để xác định vectơ cường độ điện trường do toàn bộ vật mang điện gây ra tại M.

Chú ý, vectơ cường độ điện trường tổng hợp thu được sau khi áp dụng nguyên lí chồng chất điện trường là một biểu thức tích phân vectơ. Do đó, ta phải tìm cách chuyển biểu thức tích phân vectơ về biểu thức tích phân đại số để có thể tính toán được.

Nếu các vectơ d E do dQ sinh ra là không thay đổi phương chiều khi dQ chạy trên toàn bộ vật dẫn thì theo quy tắc cộng vectơ ta chỉ cần chuyển biểu thức tích phân vectơ về biểu thức tích phân đại số thông thường.

Nếu các vectơ d E thay đổi phương chiều khi dQ chạy trên toàn bộ vật

dẫn thì ta cần tách d E thành hai thành phần vuông góc với nhau, khi đó ta chuyển biểu thức tích phân vectơ về hai biểu thức tích phân đại số trên hai

thành phần vuông góc của d E. Từ đó, dựa trên tính chất đối xứng, ta lựa chọn cách chia vật thành các phần tử điện tích điểm sao cho việc tính tích phân thuận lợi nhất.

Bước 1: Chia vòng dây thành các phần tử điện tích điểm dQ và xác định vectơ cường độ điện trường d E do điện tích điểm đó gây ra tại M.

Cường độ điện trường do vòng dây gây ra tại một điểm nào đó bằng tổng các cường độ điện trường d E do các phân tử điện tích dQ nằm trên vòng dây gây ra. Tại điểm M cường độ điện trường do phần tử điện tích dQ gây ra là:



d E k

dQ r

r3

Với độ lớn dE k dQ , phương và chiều như hình vẽ.

r2

Bước 2: Áp dụng nguyên lý chồng chất điện trường, cường độ điện trường tại M bằng:



E M 



vòng



d E 



vòng

k dQ r

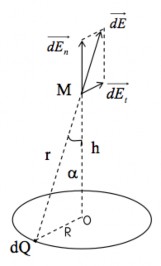
r3

Bước 3: Phân tích vectơ d E thành hai thành phần vuông góc d Et và d En . Chuyển biểu thức tích phân vectơ về biểu thức tích phân đại số.

Vì các điện tích dQ phân bố đối xứng qua điểm O nên ứng với một phần tử điện tích dQ luôn tìm được một phần tử điện tích dQ* đối xứng với dQ qua O. Do