Liên Hệ Giữa Vectơ Cường Độ Điện Trường Và Hiệu Điện Thế

V Q

40r

 Điện trường gây ra bởi hệ điện tích điểm:

(1.34)

V Vi

Qi

4r

(1.35)

i i 0 i

Có thể bạn quan tâm!

• Cường Độ Điện Trường Gây Ra Bởi Một Điện Tích Điểm
• Đường Sức Của Điện Trường Gây Ra Bởi Điện Tích Điểm
• Thế Năng Của Điện Tích Trong Điện Trường
• Liên Hệ Giữa Vectơ Cường Độ Điện Trường Và Điện Thế
• Điều Kiện Cân Bằng Tĩnh Điện. Tính Chất Của Vật Dẫn Mang Điện
• Năng Lượng Tương Tác Của Một Hệ Điện Tích Điểm

Xem toàn bộ 258 trang tài liệu này.

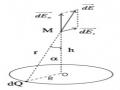
 Điện trường gây bởi một vật tích điện phân bố liên tuc Q:

V dQ

(1.35)

vât 40r

 Điện trường bất kì:



g

V Eds

M

với g là điểm gốc của thế năng.

(1.37)

Chú ý:Điện thế là đại lượng đại số (có thể âm, dương hoặc bằng không) và vô hướng.

b. Hiệu điện thế

Từ định lý về thế năng và định nghĩa điện thế, ta có:

AMN WM WN q(VM VN ) (1.38)

Vậy: Công của lưc

tin

h đi ện trong sự dic̣ h chuyển đi ện tích điểm q tư

điểm M tớ i điểm N trong điện trườ ng bằng tích số của đi ện tích q vớ i hi ệu điện thế giữa hai điểm M và N đó.

Nếu lấy q 1 thì VM VN AMN . Có nghĩa là hiệu điện thế giữa hai điểm

M và N trong điện trường là m ột đaị lươn

g bằng công của lưc

tin

h đi ện trong

sự dic̣ h chuyển một đơn vi ̣điện tích dương từ điểm M đến điểm N.

Mặt khác, nếu lấy q 1 và chọn điểm N ở xa vô cùng thì VM VAM, mà ta đã qui ước W 0 V 0 nên VM AM, tứ c là đ iện thế taị m ột điểm

trong điện trường là một đaị lươn

g về tri ̣số bằng công của lưc

tĩnh điện trong

sự dic̣ h chuyển một đơn vi ̣điện tích dương từ điểm đó ra xa vô cùng.

Chú ý:

 Đơn vi ̣đo điện thế và hiệu điện thế trong hệ SI là Vôn, kí hiệu là V.

 Trong kỹ thu ật, đaị lươn

g hi ệu điện thế đươc

sử dun

g nhiều hơn đại

lượng đi ện thế . Vì giá tri ̣của hi ệu điện thế không phu ̣thu ộc vào cách chọn gốc tính đi ện thế (hoặc thế nă ng ). Thông thường người ta chọn điện thế của đất ho ặc của những v ật nối đất bằng không . Khi đó nói

điện thế của một điểm nào đó chính là nói về hi ệu điện thế giữa điểm

đó với đất.

Bài toán 7:

Tính công của lực điện trường khi dịch chuyển dịch điện tích q  109 C

1

từ điểm C đến D nếu a  6cm, Q

10 .109C , Q

32

2.109C (Hình vẽ).

Định hướng:

Thông thường, khi tính công dịch chuyển ta

thường xuất phát từ công thức tính công theo D

định nghĩa: A F.ds. Tuy nhiên, khi tìm công a

của lực điện trường ta sẽ áp dụng định lý về thế a a

năng: AMN

WM

WN

q(VM

VN ) .

Q1 C Q2

Chú ý rằng: q là điện tích dịch chuyển. VM,N

là điện thế tại điểm M, N trong điện trường do các điện tích còn lại sinh ra. Như vậy, trước hết cần phải trả lời được câu hỏi: Tìm công của lực điện trường nào thực hiện để để dịch chuyển điện tích nào?

Giải:

Áp dụng định lý về thế năng ta có công của lực điện trường làm điện tích

q dịch chuyển từ C đến D là:

ACD WC WD q(VC VD ).

Điện thế tại C và D do hai điện tích điểm Q1 và Q2 gây ra tại C và D:

0

V V V 1

Q1  1 Q2

C C1

C 2 4a

40 a

VD VD1



VD 2 

40 a 2

1

1 Q

Q1  1 Q2

40 a 2

1 Q 1 Q

1 Q 

ACD q(VC VD ) q (12)  (12)

2

2

2

1

 40 a 40 a 40 a 40 a 

40a

2

q

ACD 

1 (Q

Q2 )

ACD 

9.109.109

36.104 .

1. 4109

2

2

3

 106

(J )

1.7. MẶT ĐẲNG THẾ

1.7.1. Định nghĩa

Mặt đẳng thế là quỹ tích của những điểm có cùng đi ện thế ở trong đi ện trường (V = const).

Ví dụ: mặt đẳng thế trong điện trường gây ra bởi một điện tích điểm là những mặt cầu có tâm nằm tại vị trí đặt điện tích điểm đó.

1.7.2. Tính chất mặt đẳng thế

Công của lưc

tin

h đi ện trong sự dic̣ h chuyển m ột điện tích bất kỳ trên

một mặt đẳng thế bằng không.

Thưc

v ậy, với hai điểm M và N bất kỳ trên m ặt đẳng thế (VM VN ) thì

công của lưc

tin

h điện khi dic̣ h chuyển điện tích q giữa hai điểm này sẽ bằng:

AMN q(VM VN )  0

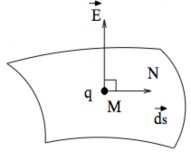
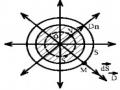
Tại mọi điểm trên m ặt đẳng thế , véctơ cườ ng đ ộ điện trườ ng có phươ ng vuông góc vớ i m ặt đẳng thế . Nghĩa là các đường sứ c đi ện trường luôn vuông góc với các mặt đẳng thế.

Giả sử dưới tác dụng của lực tĩnh đi ện, điện tích q trên mặt đẳng thế dic̣ h chuyển từ điểm M

43

Hình 1.14

đến một điểm N rất gần đó, tứ c là véctơ dic̣ h chuyển ds MN . Khi đó theo

tính chất trên, công của lưc

tin

h điện bằng:

N N

AMN Fds qEds  0

M M

Ta suy ra E ds. Vì ds là véctơ bất kỳ trên m ặt đẳng thế nên véctơ cường độ điện trường E vuông góc với mặt đẳng thế tại mọi điểm của mặt đó (Hình 1.14).

1.8. LIÊN HỆ GIỮA VECTƠ CƯỜNG ĐỘ ĐIỆN TRƯỜNG VÀ HIỆU ĐIỆN THẾ

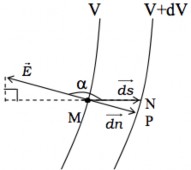
Xét hai điểm M và N rất gần nhau trong điện trường: điểm M thuộc mặt đẳng thế có điện thế V, còn điểm N thuộc mặt đẳng thế có điện

thế V+dV (với dV>0). Giả sử dưới tác dụng của

lưc

tin

h điện, một điện tích q < 0 dịch chuyển từ

điểm M đến điểm N nói trên . Khi đó công của

lưc

tin

h điện trong dic̣ h chuyển này bằng:

dA qEds, ds MN

Hình 1.15

Mặt khác: dA q(VM VN ) q{V  (V dV )} qdV

Eds dV (1.39)

Gọi  (E, ds) khi đó Eds Eds cosEsds dV  0

dV



Es ds

Kết luận:

44

cos 0

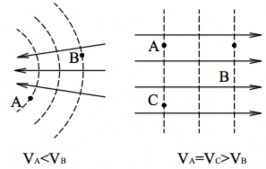
Hình 1.16

Véctơ cườ ng độ điện trườ ng E luôn luôn hướ ng theo chiều giảm của điện thế (góc tù).

Hình chiếu của E lên một phươ ng nào đó về tri ̣số bằng đ ộ giảm điện thế trên một đơ n vi ̣dài của phươ ng đó:

E dV

s ds

(1.40)

Trong hệ tọa độ Descartes:



Ex



dV

dx

   

 

E dV

E (i dV j dV k dV ) E gradV (1.41)

y





Ez

dy

dV

dz

dx dy dz

Lân cận một điểm trong đi ện trườ ng , điện thế biến thiên nhiều (nhanh) nhất theo phươ ng pháp tuyến vớ i m ặt đẳng thế (hay theo phương của đường sức đi ện trường vẽ qua điểm đó ) vì khi đó

 0, cos1 (max).

Bài toán 8:

Một khối cầu tâm O bán kính R tích điện dương với điện tích Q được phân bố đều theo thể tích. Chọn gốc tính điện thế ở vô cực, hãy xác định:

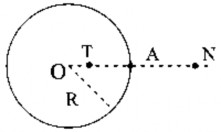
a. Điện thế tại điểm A ở trên mặt cầu.

b. Điện thế tại tâm O.

c. Điện thế tại điểm T ở trong khối cầu.

d. Điện thế tại điểm N ở ngoài khối cầu.

Giải:

Trong bài toán, dung định lý O – G ta đã xác định được điện trường trong lòng và bên ngoài khối cầu với kết quả như sau:



E tr (trong )





r , r

0

3

R ,  3Q

4R 3

(*)

a. Tính VA :



E ng (ngoài) k

Q

r 3 r ,

r R (**)

Xét dọc theo một phương trình bán kính, áp dụng biểu thức (*) cho A là một điểm trên mặt khối cầu, ta có:

dV E dr E dr r dr

r tr

30

0

A R

Từ đó:

dV 3

rdr

0 0

hay:

R2

V0 VA

60

Suy ra:

R2

VA V0

60

Vì Q 4 R3 , nên

3

R2 

3Q

4R

và ta sẽ có:

VA V0

 1

40

Q

2R

V0

kQ

2R

Nếu xem A là thuộc ngoài khối cầu thì tương tự cách tính trên, ta có:

kQ dr kQ

VA VEng dr 

r2

R

Vì ở vô cùng V 0

A R

nên suy ra

V kQ

A R

Vậy khối cầu tích điện đều với điện tích tổng cộng Q gây ra điện thế tại bề mặt có giá trị như điện thế gây bởi một điện tích điểm Q đặt tại tâm O.

b. Tính V0 :

Vì điện thế là hàm liên tục nên điện thế tại A sát mặt cầu nằm bên trong và nằm bên ngoài khối cầu phải bằng nhau:

0

V kQ V

A R

V  3kQ

kQ

2R

0 2R

c. Tính VT :

Tính tương tự như trên, ta có:



rT

r 2

V0 VT Etr dr rdr T

A

r 2

30

3kQ

0

r 2

60

VT V0 TT

60 2R 60

Vậy khi đi từ tâm O ra đến bề mặt của khối cầu tích điện đều, điện thế giảm dần theo hàm mũ.

d. Tính VN



kQ dr kQ

Do đó:

VN VEng dr 

rS

2 r

r

N

r

S

Nhận xét:

V kQ

N

rN

 Trong trường hợp điện thế

Q  0 , điện thế V0

tại tâm O là cực đại rồi

giảm dần theo hàm mũ ra đến bề mặt. Điện thế bề mặt là một hằng số, ra ngoài khối cầu điện thế giảm theo quy luật tỉ lệ nghịch với khoảng cách.

Ở vô cực V 0 (V cực tiểu).

 Trong trường hợp điện tích khối cầu tiểu.

Q  0

thì V0

cực tiểu, còn Vcực

TỔNG KẾT CHƯƠNG 1

1. Định luật Coulomb

a. Phát biểu

Lưc

tươ ng tác giữa hai đi ện tích điểm đứ ng yên trong chân không có

phương nằm trên đường thẳng nối hai đi ện tích, có chiều đẩy nhau nếu hai điện tích cùng dấu và hút nhau nếu hai điện tích trái dấu, có độ lớ n tỉ lệ thuận vớ i tích độ lớ n của hai điện tích và tỉ l ệ nghịch với bình phương khoảng cách

giữa chúng.

b. Biểu diễn vectơ

1

F 

2

 q.q0r

trong đó:

40 r r

F là lực tĩnh điện do điện tích q tác dụng lên điện tích q0 (điểm đặt lực trên q0);

r là vectơ nối từ điện tích điện tích q đến q0;

ε là hằng số điện môi, ε =1 đối vớ i chân không.

2. Khái niệm điện trường

Điện trường là một dạng đặc biệt của vật chất bao quanh các điện tích. Khi đặt một điện tích vào trong không gian thì không gian bao quanh điện tích tồn tại một điện trường, và điện trường này sẽ tác dụng lực điện lên các điện tích khác đặt trong nó.

3. Vectơ cường độ điện trường

a. Định nghĩa

Vectơ cường đ ộ điện trường E tại một điểm là đai

lươn

g đ ặc trưng cho

điện trườ ng tai

điểm đó về phươ ng di ện tác dun

g lưc

, có tri ̣véctơ bằng lưc

tác dun

g của điện trườ ng lên một đơ n vi ̣điện tích dươ ng đặt tai

điểm đó:

F



E 

q

b. Vectơ cường độ điện trường gây ra bởi điện tích điểm

Xem tất cả 258 trang.