Thế Năng Của Điện Tích Trong Điện Trường

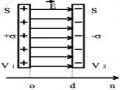
qi. dV divD. dV

i (V ) (V )

divD (1.24)

Biểu thức (1.24) là dạng vi phân của định lý O-G.

1.5.4. Phương pháp sử dụng định lý O-G

Khi điện trường có tính chất đối xứ ng (đối xứ ng cầu , đối xứ ng tru ̣, đối xứ ng phẳng ), để xác định véctơ E hay véctơ D của đi ện trường đó thì áp

dụng định lý O -G là phương pháp đơn giản , ngắn gon hơn phương pháp tính

Có thể bạn quan tâm!

• Vật lý đại cương 2 - 2
• Cường Độ Điện Trường Gây Ra Bởi Một Điện Tích Điểm
• Đường Sức Của Điện Trường Gây Ra Bởi Điện Tích Điểm
• Liên Hệ Giữa Vectơ Cường Độ Điện Trường Và Hiệu Điện Thế
• Liên Hệ Giữa Vectơ Cường Độ Điện Trường Và Điện Thế
• Điều Kiện Cân Bằng Tĩnh Điện. Tính Chất Của Vật Dẫn Mang Điện

Xem toàn bộ 258 trang tài liệu này.

theo nguyên lý chồng chất đi ện trường . Ta thưc đây:

hi ện tuần tự các bước sau

Bước 1: Nhận xét về sự đối xứ ng trong sự phân bố của hệ điện tích.

Bước 2: Xác điṇ h daṇ g đối xứ ng của h ệ đường sứ c và xác điṇ h quỹ tích những điểm mà các véctơ D (hoặc véctơ E ) có cùng độ lớn và bằng với D hoặc E tại điểm ta cần khảo sát.

Bước 3: Xây dưn

g mặt kín S (gọi là mặt Gauss) là quỹ tích nói trên. Nếu

quỹ tích đó chưa tạo thành m ặt kín thì ta làm kín laị bằng các m ặt khác tùy ý sao cho việc tính toán là đơn giản nhất.

Bước 4: Tính từ ng vế của biểu thứ c (1.23) để rút ra đại lượng cần xác điṇ h.

Bài toán 5:

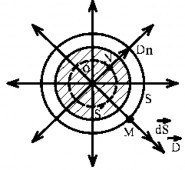
Xác điṇ h cường độ điện trường E gây bởi một khối cầu tâm O, bán kính R, tích điện đều với m ật độ điện khối > 0 tại một điểm ở bên ngoài và taị một điểm ở bên trong lòng khối cầu đó.

Giải:

Đối với điểm M ở ngoài khối cầu, cách tâm

O một khoảng r R .

Bước 1: Vì khối cầu tích điện đều nên hệ

đường sức có tính chất đối xứng cầu.

Bước 2: Hệ đường sức trùng với các bán kính, hướng ra ngoài. Do đó, quỹ tích của những điểm có độ lớn | D | bằng nhau và bằng | DM |là mặt cầu S

tâm O, bán kính r đi qua điểm M. Trên mặt cầu S ta có

Bước 3: Mặt kín S chính là mặt cầu S.

Bước 4: Áp dụng định lý O – G.

D DM const .

  n

D.d S

S

Khai triển vế trái:

qi

i 0

Tại mọi điểm trên mặt S ta có:

D   d S và

D Dn const

Dd S

D dS D dS

D.4r 2

( S )

Triển khai vế phải:

( S )

( S )

qi

i

là tổng điện tích của khối cầu (bán kính R ) nằm trong S và bằng:

qi

Q 4R3

3

i

Ghép hai vế lại ta có:

2 4R3

D.4r 

3

R3

Rút ra:

D 3r2 , r R,

và dạng vectơ: Hay:



D 



D 

R 3 

r

3r 3

Q r, r R

4r 2 r



DkQ r

(1.25)

0

E 

r 2 r

Kết quả này giống với biểu thức tính cường độ điện trường của một điện tích đặt tại O.

Bây giờ ta lại tính đối với điểm N nằm trong lòng khối cầu ( r R ).Vẽ mặt cầu Stâm O, đi qua điểm N. Lập lại các lí luận như trên ta thu được kết quả sau:

Do vậy,



D 



1

r 

3

Q

4R 3



r ; r R

0

 1 

kQ r (1.26)

Nhận xét:

E  3

r R 3

Ta thấy cường độ điện trường ở trong lòng và ở ngoài quả cầu biến thiên theo hai quy luật.

 Ở trong ( r R ): điện trường tăng theo r với quy luật tuyến tính.

 Ở ngoài ( r R ): điện trường giảm theo r

với quy luật tỉ lệ nghịch với

 Tại bề mặt khối cầu:

E(R) R

r 2 .

kQ

0

3R2

Mở rộng:

Nếu khối cầu tích điện âm (  0 ) thì các kết quả thu được vẫn giống như (1.25) và (1.26), chỉ có khác là E N , E M và hệ đường sức điện cảm ngược chiều với vector bán kính r , tức là chúng hướng vào tâm O.

Nếu đây là một mặt cầu (rỗng) hoặc một vật dẫn (xem chương 2) tích điện đều thì:

 Ở ngoài ( r R ) kết quả (1.25) vẫn đúng vì

qiQ .

i

 Ở trong ( r R ) vì

Bài toán 6:

qi 0

i

nên E trong  0.

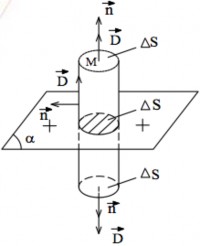
Xác định điện trường của một mặt phẳng vô hạn tích điện đều với mật độ điện mặt  0 .

Giải:

Vì điện tích phân bố đối xứng phẳng nên vector cảm ứng điện D tại một điểm bất kỳ

trong điện trường sẽ có phương vuông góc với mặt phẳng mang điện, hướng

ra xa khỏi mặt phẳng và độ lớn của | D | chỉ có thể phụ thuộc vào khoảng cách từ điểm đang xét tới mặt phẳng. Dễ dàng nhận thấy quỹ tích những điểm có cùng độ lớn của cường độ điện trường là hai mặt phẳng cùng song song và cách đều mặt phẳng tích điện.

Do đó, để xác định vector cảm ứng điện D tại một điểm M, ta vẽ mặt kín S (mặt Gauss) như sau: Vẽ qua M một trụ kín mà điểm M thuộc vào một

trong hai mặt đáy có diện tích là S , cả hai mặt đáy cùng song song và cách

đều mặt phẳng tích điện, còn các đường sinh thì vuông góc với mặt phẳng.

Nhận xét là tại mọi điểm trên hai mặt đáy ta thấy D   n , còn ở những điểm trên mặt bên thì D vuông góc với n .

Khi đó vế trái của (1.23) được triển khai thành:

Dd S

( s )

mat bên DndS hai day DndS

Mọi điểm trên hai trên hai đáy Dn D const , ta thấy D   n , còn ở

mọi điểm trên mặt bên thì D vuông góc với n , Dn  0 , do đó:

Dd S

( S )



hai day

Dn dS

D.2S

Ở vế phải của (1.23), qilà tổng điện tích có trong mặt trụ kín này; đó

i

chính là điện tích của mặt phần mặt phẳng được cắt bởi mặt trên hình trụ nên

ở đây qi.S .

i

Ghép hai vế lại, ta có:

D.2S .S

rút ra:

D 

2

hay:



D 





n

2

 (1.27)

0

E 2n

trong đó n là vector pháp tuyến đơn vị của mặt phẳng tích điện đang khảo sát.

Nhận xét:

 Các vector D (và E ) không phụ thuộc vào khoảng cách từ điểm M đến mặt phẳng nên điênn trường ở đây là điện trường đều E const .

 Điện trường do mặt phẳng hữu hạn tích điện đều tạo ra ở những vị trí rất gần mặt đó cũng được xem như là đều.

 Nếu mặt phẳng tích điện âm thì kết quả thu được cũng như vậy song các vector D , E tại hướng vào mặt phẳng tích điện.

1.6. ĐIỆN THẾ

1.6.1. Công của lực tĩnh điện

Xét điện tích điểm q đặt trong điện trường tin

h gây bởi đi ện tích điểm Q

(+) đứ ng yên. Giả sử điện tích q di chuyển theo m ột đường cong MN (Hình 1.13). Trong quá trình dịch chuyển, điện tích q luôn chịu tác dụng của lực tĩnh

điện gây ra bởi điện trường của Q. Ta hãy tính công của lưc

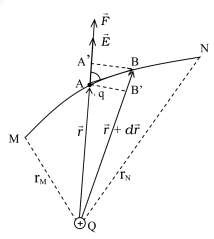
trong quá trình dic̣ h chuyển này.

Giả sử ở thời điểm t điện tích q có vi ̣trí

tin

h điện sinh ra

là điểm A trên quỹ đao

MN. Tại đó lực tĩnh

điện tác dung lên điện tích q là:

1



 q.Q r

F

40 r r

2

Sau thời gian dt, điện tích q thưc

hi ện

chuyển dời vô cùng nhỏ tới điếm B trên quỹ

đaọ . Véctơ dic̣ h chuyển ds AB dr . Trên chuyển dời vô cùng nhỏ này có thể xem như

Hình 1.13

E const , do đó công nguyên tố của lưc

tin

h đi ện F trong chuyển dời vi

phân này đươc

tính là:

dA F.ds

1



qQ r 



2

0

1 qQ d(r)2

1 qQ r

2

dA 

40 r

.dr 

r

40 r

r  4r2 r dr

dA 1 40

qQ dr r2

Vậy công của lưc đến N sẽ bằng:

tin

h đi ện trong sự dic̣ h chuyển của đ iện tích q từ M

N N 1 qQ

AMN dA 4r2 dr

AMN

M M

qQ ( 1 40 rM

0

1 )

rN

AMN

qQ

40rM

qQ

40rN

(1.28)

Thay vì điện tích Q, bây giờ tao

ra trường tin

h đi ện là một hệ điện tích

điểm đứ ng yên Q1, Q2,...., Qn. Bằng cách áp dun

g nguyên lý chồng chất điện

trường và cách tính tương tự như trên, ta sẽ thu đươc kêt́ quả:

AMN

qQi



i 40riM

qQi



i 40riN

(1.29)

trong đó riM và riN lần lươt

Nhận xét:

là khoảng cách từ điện tích Qi đến các điểm M và N.

 Công của lực tĩnh điện không phụ thuộc vào hình dạng của quỹ đạo dịch chuyển mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối.

 Nếu q dịch chuyển theo một đường cong kín (rM = rN) thì công của lưc̣

tĩnh điện A qEds  0 hay

Vậy:

Eds  0 .

Trường tĩnh điện là trường lực thế.

 Lưu số của vectơ cường độ điện trường (tĩnh) dọc theo đường cong kín ( Eds ) bằng không.

1.6.2. Thế năng của điện tích trong điện trường

a. Điện trường gây ra bởi một điện tích điểm

Do trường tĩnh điện là một trường lực thế nên tồn tại khái niệm thế năng (trang 88 - VLĐC1).

Theo định lý về thế năng:

AMN

WM

WN

qQ

40rM

qQ

40rN

WM

qQ C

40rM

Quy ước chon thế nă ng ở vô cùng là bằng không (W∞ = 0). Vậy thế năng

do trường tĩnh điện của điện tích Q tác dụng lên điện tích q đặt cách Q một khoảng r là:

W qQ

40r

(1.30)

Như vậy, thế năng có thể âm hoặc dương tùy thuộc vào dấu của qQ.

 Nếu qQ  0 W  0

 Nếu qQ  0 W  0

b. Điện trường gây ra bởi một hệ điện tích điểm

W Wi

i

qQi



i 40ri

(1.31)

c. Điện trường bất kì

WM WM Wg AMg

trong đó: g là điểm gốc thế năng (Wg=0).

g

WM qEds

M

(1.32)

1.6.3. Điện thế và hiệu điện thế

a. Điện thế

Nhận xét:

Tỉ số W/q không phu ̣ thuộc vào độ lớn của điện tích q mà chỉ phu ̣thu ộc vào các điện tích gây ra điện trường và vi ̣trí của điểm đang xét. Như vậy, W/q đặc trưng cho điện trường về phương diện năng lượng tại điểm được xét đại

lượng này được gọi là điện thế.

Định nghĩa:

Điện thế là đại lượng đặc trưng cho điện trường tại điểm đang xét có giá trị xác định bởi biểu thức:

V W

q

(1.33)

Biểu thứ c tính điện thế của điện trư ờng cho một số trư ờng hơp:

 Điện trường gây ra bởi điện tích điểm: