Định Luật Về Tác Dụng Độc Lập Của Các Tia Sáng

CÂU HỎI LÝ THUYẾT

1. Phát biểu luận điểm 1 của Maxwell. Phân biệt sự khác nhau giữa điện trường tĩnh và điện trường xoáy.

2. Thiết lập phương trình Maxwell – Faraday dưới dạnh tích phân và dạng vi phân.

3. Phát biểu luận điểm 2 của Maxwell. Nêu khái niệm dòng điện dịch và phân biệt giữa dòng điện dịch và dòng điện dẫn.

4. Thiết lập phương trình Maxwell – Amper dưới dạnh tích phân và dạng vi phân.

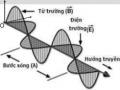
5. Nêu bản chất của trường điện từ và sóng điện từ.

6. Phân biệt sự giống và khác nhau giữa sóng điện từ và song cơ học.

7. Thế nào là sóng phẳng đơn sắc, nêu tính chất của sóng phẳng đơn sắc.

8. Phân loại sóng điện từ phẳng đơn sắc.

Có thể bạn quan tâm!

• Luận Điểm Maxwell Thứ Hai. Dòng Điện Dịch
• Trường Điện Từ Và Hệ Phương Trình Maxwell
• Các Phương Trình Của Trường Điện Từ (Hệ Phương Trình Maxwell):
• Những Phát Biểu Tương Đương Của Định Luật Descartes
• Các Đại Lượng Trắc Quang Là Các Đại Lượng Dùng Trong Kĩ Thuật Đo Lường Ánh Sáng.
• Gương Fresnel Hình 2.10. Lưỡng Thấu Kính Bile

Xem toàn bộ 258 trang tài liệu này.

BÀI TẬP CHƯƠNG 5

Bài 5.1.

Một tụ điện có hằng số điện môi  4 , được mắc vào một điện áp xoay chiều: u  200 2 cos(100t )V . Viết biểu thức mật độ dòng điện dịch chạy

4

giữa khoảng không gian của hai bản tụ điện. Biết hai bản tụ điện cách nhau

d  2 mm.

Bài 5.2.

Điện trường giữa hai bản của một tụ điện biến đổi theo quy luật:

E  2.102 cos(100t ) (V / cm) . Khoảng cách giữa hai bản tụ là d  2 mm;

4

điện dung của tụ điện C  2.104 pF . Xác định giá trị cực đại của dòng điện dịch.

Bài 5.3.

Xác định mật độ dòng điện dịch trong một tụ điện phẳng khi hai bản của tụ điện được dịch chuyển song song ra xa nhau với vận tốc tương đối v , nếu:

a. Điện tích trên mỗi bản không đổi.

b. Hiệu điện thế trên hai bản không đổi.

Biết khoảng cách d giữa hai bản trong khi dịch chuyển rất nhỏ so với kích thươc của hai bản.

Bài 5.4.

Trong mạch dao động LC, dòng điện chạy trong cuộn dây có biểu thức:

i  2 2 cos(100t ) (A). Hệ số tự cảm của cuộn dây là L 1H . Tìm:

4

a. Chu kì dao động của dòng điện.

b. Năng lượng điện trường của mạch tại thời điểm ban đầu.

c. Năng lượng từ trường cực đại.

Bài 5.5.

Sóng điện từ lan truyền trong môi trường bất kì tần số f  50 Hz và tốc độ truyền sóng v  2, 5.108 m / s. Xác định bước sóng của sóng điện từ trong môi trường đó. Nếu lan truyền trong chân không bước sóng của sóng điện từ nói trên sẽ là bao nhiêu?

PHẦN IV. QUANG HỌC

Quang học là môn học nghiên cứu về ánh sáng và tương tác của ánh sáng với các chất khác. Quang học được chia làm hai phần: Quang học cổ điển và quang học lượng tử.

Quang học cổ điển bao gồm quang hình học và quang học sóng. Cuối thế kỉ XVII Newton dựa vào tính chất truyền thẳng của ánh sáng đã đưa ra thuyết hạt về ánh sáng. Theo Newton ánh sáng là một dòng các hạt bay ra từ vật phát sáng theo các đường thẳng. Cùng thời gian đó Huygens lại đưa ra thuyết sóng về ánh sáng. Theo ông, ánh sáng là sự truyền những dao động đàn hồi trong một môi trường gọi là “êtê vũ trụ”. Do uy tín khoa học của Newton nên thế kỉ XVIII là thời kì thống trị của thuyết hạt về ánh sáng. Tuy nhiên vào đầu thế kỉ XIX trên cơ sở các giả thuyết sóng về ánh sáng. Fresnel đã giải thích đầy đủ các hiện tượng quang học được biết thời đó. Kết quả là thuyết sóng được mọi người công nhận và thuyết hạt hầu như bị lãng quên. Sau khi thuyết điện từ của Maxwell ra đời năm 1864 người ta đã chứng minh được rằng ánh sáng là các sóng điện từ bước sóng từ 0, 38m đến 0, 76m .

Vào cuối thế kỉ XIX và đầu thế kỉ XX hàng loạt sự kiện thực nghiệm đã chứng tỏ rằng mọi vật phát xạ hay hấp thụ ánh sáng theo những lượng gián đoán. Điều đó lại dẫn đến khái niệm hạt ánh sáng: Ánh sáng gồm một dòng các hạt gọi là các photon. Sự phát triển của vật lí về sau đã chứng tỏ rằng ánh sáng vừa có tính chất sóng vừa có tính chất hạt. Trong một số hiện tượng như giao thoa, nhiễu xạ, phân cực, ánh sáng thể hiện tính chất sóng; còn trong một số hiện tượng khác như hiệu ứng quang điện, hiệu ứng Compton, ánh sáng lại thể hiện tính chất hạt.

Trong phần này của giáo trình chúng ta sẽ nghiên cứu các cơ sở của quang học - nhằm hiểu rò bản chất của ánh sáng, đồng thời cũng tìm hiểu ứng dụng những định luật quang học trong kĩ thuật và đời sống.

Chương 1. CƠ SỞ CỦA QUANG HÌNH HỌC. CÁC ĐẠI LƯỢNG TRẮC QUANG

Quang hình học được nghiên cứu xuất phát từ khái niệm về các tia sáng. Phần quang học dựa trên khái niệm đó gọi là quang hình học. Dựa vào các định luật cơ bản về các tia sáng: Định luật truyền thẳng của ánh sáng; định luật khúc xạ và phản xạ của ánh sáng.

1.1. CÁC ĐỊNH LUẬT CƠ BẢN CỦA QUANG HÌNH HỌC

Quang hình học nghiên cứu ánh sáng dựa trên bốn định luật cơ bản sau đây:

1.1.1. Định luật về sự truyền thẳng của ánh sáng

Trong một môi trường trong suốt đồng tính và đẳng hướng ánh sáng truyền theo đường thẳng. Phương truyền thẳng của ánh sáng gọi là tia sáng tập hợp các tia sáng gọi là chùm tia sáng. Có ba loại chùm tia sáng là: chùm hội tụ; chùm phân kì và chùm song song.

Khi nghiên cứu hiện tượng nhiễu xạ ta sẽ thấy khi ánh sáng truyền qua những lỗ thật nhỏ hoặc gặp những chướng ngại vật kích thước nhỏ vào cỡ bước sóng ánh sáng thì định luật trên không còn đúng nữa.

Ứng dụng định luật truyền thẳng của tia sáng có thể giải thích được một số hiện tượng như nhật thực, nguyệt thực …

1.1.2. Định luật về tác dụng độc lập của các tia sáng

Tác dụng của các chùm ánh sáng khác nhau thì độc lập với nhau, nghĩa là tác dụng của một chùm sáng này không phụ thuộc vào sự có mặt hay không của các chùm sáng khác.

1.1.3. Hai định luật của Descartes

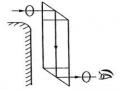
Thực nghiệm xác nhận rằng khi một tia sáng OI tới mặt phân cách hai môi trường trong suốt, đồng tính và đẳng hướng thì tia sáng bị tách thành hai tia: tia phản xạ IR1 và tia khúc xạ IR2 (Hình l.l) tuân theo hai định luật sau đây:

a. Định luật Descartes thứ nhất:

Tia phản xạ nằm trong mặt phẳng tới (mặt phẳng chứa tia tới và pháp tuyến) và góc tới bằng góc phản xạ.

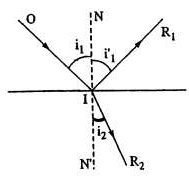
i1 i'1 ( l.l )

b. Định luật Descartes thứ hai:

Tia khúc xạ nằm trong mặt phẳng tới ở phía bên kia pháp tuyến tại điểm tới, đối với mỗi cặp môi trường nhất định tỉ số giữa sin góc tới (sin i1 ) và sin

góc khúc xạ (sin i2 ) là một số không đổi.

sin i

Hình 1.1. Định luật phản xạ và định luật khúc xạ

21

1n

sin i2

( l.2)

trong đó n21 là một số không đổi phụ thuộc vào bản chất của hai môi trường và được gọi là chiết suất tỉ đối của môi trường 2 đối với môi trường 1.

Nếu n21  1 thì i2 i1 tia khúc xạ gần pháp tuyến và môi trường 2 được gọi là chiết quang hơn môi trường 1. Ngược lại nếu n21  1 thì i2 i1, tia khúc xạ lệch xa pháp tuyến hơn và môi trường 2 kém chiết quang hơn môi trường 1

c) Chiết suất tỉ đối và chiết suất tuyệt đối: Nếu gọi v1 và v2 là vận tốc ánh sáng trong môi trường (1) và (2) thì thực nghiệm chứng tỏ:

n21

v1 v2

(l.3)

Với nước - không khí: n21 =1,33; thuỷ tinh - không khí: n21 =1,52.

Ngoài chiết suất tỉ đối, người ta còn định nghĩa chiết suất tuyệt đối của

một môi trường. Theo định nghĩa chiết suất tuyệt đối của một môi trường là chiết suất tỉ đối của môi trường đó đối với chân không. Nếu gọi v là vận tốc ánh sáng trong môi trường, c là vận tốc ánh sáng trong chân không và n là chiết suất tuyệt đối của môi trường thì căn cứ vào (l.3) ta có :

n c

v

(l.4)

Đối với không khí v  c nên n  1 . So sánh với kết quả thu được khi



nghiên cứu vận tốc truyền sóng điện từ, ta có: n 

lượt là hằng số điện môi và độ từ thẩm của môi trường.

. Trong đó  và  lần

Ta tìm liên hệ giữa chiết suất tỉ đối của hai môi trường và chiết suất tuyệt đối của chúng. Từ ( l -3 ) có thể viết :

n v1 c

: c n1

(l.5)

v

v

21

2 2 1 2

v

n

Nếu môi trường thứ nhất là không khí thì n1  1 và n21  n2. Do đó có thể coi chiết suất tuyệt đối của một môi trường là chiết suất tỉ đối của môi trường đó đối với không khí.

d) Hiện tượng phản xạ toàn phần

Xét hai môi trường 1 và 2. Nếu n21>1 thì i2<il và mọi tia tới đều cho tia khúc xạ, ví dụ trường hợp ánh sáng đi từ không khí vào nước Hình l.2a.

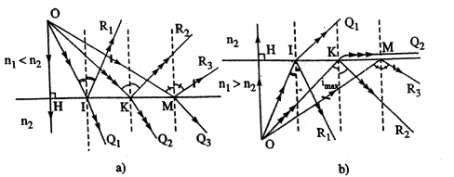
Hình 1.2. Hiện tượng phản xạ toàn phần

Nếu n21  1 thì i2 i1 và không phải mọi tia tới đều cho tia khúc xạ. Vì

góc khúc xạ i2 chỉ có thể nhỏ hơn  do đó, chỉ những tia tới nào mà góc tới il

2

ứng với góc khúc xạ i2  ; mới cho tia khúc xạ. Gọi imax là góc tới ứng với

2

góc khúc xạ bằng

 , căn cứ vào định luật khúc xạ ta có: 2

sin imax= n21 ( l.6 )

Nếu il > imax thì toàn bộ ánh sáng đều bị phản xạ và không còn tia khúc xạ nên. Lúc đó ta có hiện tượng phản xạ toàn phần Hình l.2b. Vậy muốn xảy ra hiện tượng phản xạ toàn phần thì ánh sáng truyền từ môi trường có chiết suất lớn sang môi trường có chiết suất bé, đồng thời góc tới phải lớn hơn imax; imax được gọi là góc tới hạn. Ví dụ trong trường hợp ánh sáng truyền từ nước

ra không khí thì imax= 49o.

Hiện tượng khúc xạ và phản xạ toàn phần có nhiều ứng dụng trong thực tế.

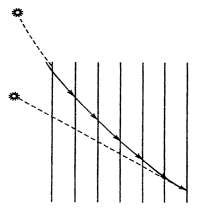
Trong thiên văn học khi xác định vị trí của các ngôi sao cần phải xét đến sự khúc xạ của ánh sáng qua các lớp không khí.

Chúng ta biết rằng chiết suất của không khí phụ thuộc mật độ của nó. Càng lên cao mật độ không khí càng giảm và do đó chiết

Hình 1.3. Độ cao quan sát và độ cao thực của ngôi sao

suất của không khí cũng bị giảm theo. Tia sáng xuất phát từ một ngôi sao nào đó không ở đỉnh đầu đi đến Trái Đất qua các lớp không khí với chiết suất tăng dần sẽ bị cong đi Hình1.3. Kết quả là vị trí quan sát được của ngôi sao ở cao hơn vị trí thực. Một ngôi sao ở đường chân trời, do hiện tượng khúc xạ ánh sáng, bị nâng lên một góc cỡ 36'.

Xem tất cả 258 trang.