Áp dụng định lý Amper về dòng điện toàn phần ta có:
H dl
C
Itp
Thay Itp rút từ biểu thức (5.18) vào biểu thức trên ta viết được:
Hdl
Có thể bạn quan tâm!
-
 Định Luật Cơ Bản Của Hiện Tượng Cảm Ứng Điện Từ
Định Luật Cơ Bản Của Hiện Tượng Cảm Ứng Điện Từ -
 Định Luật Cơ Bản Về Hiện Tượng Cảm Ứng Điện Từ
Định Luật Cơ Bản Về Hiện Tượng Cảm Ứng Điện Từ -
 Luận Điểm Maxwell Thứ Hai. Dòng Điện Dịch
Luận Điểm Maxwell Thứ Hai. Dòng Điện Dịch -
 Các Phương Trình Của Trường Điện Từ (Hệ Phương Trình Maxwell):
Các Phương Trình Của Trường Điện Từ (Hệ Phương Trình Maxwell): -
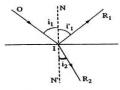
 Định Luật Về Tác Dụng Độc Lập Của Các Tia Sáng
Định Luật Về Tác Dụng Độc Lập Của Các Tia Sáng -
 Những Phát Biểu Tương Đương Của Định Luật Descartes
Những Phát Biểu Tương Đương Của Định Luật Descartes
Xem toàn bộ 258 trang tài liệu này.
D
(5.19)
(J dan
C S
t )dS
Phương trình (5.19) là phương trình Maxwell – Amper biểu diễn mối liên hệ định lượng giữa từ trường H và các dòng điện dẫn, dòng điện dịch gây ra từ trường đó.
5.3. TRƯỜNG ĐIỆN TỪ VÀ HỆ PHƯƠNG TRÌNH MAXWELL
5.3.1. Trường điện từ
Theo các luận điểm Maxwell, từ trường biến thiên làm xuất hiện điện trường biến thiên và điện trường biến thiên lại sinh ra từ trường biến thiên. Từ trường biến thiên và điện trường biến thiên không tách biệt nhau mà thống nhất lại thành trường điện từ. Trường điện từ là một dạng đặc biệt của vật chất. Nó có mang năng lượng, ngoài ra trong cơ học lượng tử còn thấy, trường điện từ mang cả khối lượng và động lượng nữa. Năng lượng trường điện từ bao gồm năng lượng của điện trường và năng lượng của từ trường tạo thành. Mật độ năng lượng của trường điện từ bằng tổng mật độ năng lượng điện trường và từ trường. Ta viết được:
0
Mặt khác:
w wđ
wt
0
12
E2 H 2
(5.20)
D 0 E ; B 0 H
Nên (5.20) được viết lại thành:
w 1
(ED BH )
2
Vậy biểu thức năng lượng cho trường điện từ trong thể tích không gian có trường:
W 1
(5.21)
(BH ED)dV
V 2
5.3.2. Hệ các cặp phương trinh Maxwell dưới tích phân
a. Cặp thứ nhất gồm:
Edl B
(5.22)
t
dS
C S
Trong đó mặt S tựa trên đường cong kín (C). Công thức (5.22) cho chúng ta biết mọi từ trường B biến thiên theo thời gian đều làm xuất hiện một điện trường xoáy E .
B dS 0
S
(5.23)
Công thức (5.22) phát biểu: từ thông gì qua mặt S kín bất kỳ bằng không. Nó nói lên từ thông đi vào mặt kín S về độ lớn bằng từ thông đi ra khỏi mặt kín đó.
b. Cặp thứ hai gồm:
H dl
D
(5.24)
(Jdan
C S
t )dS
trong đó mặt S lựa trên đường cong kín (C). Công thức (5.24) nói lên, điện trường D biến thiên theo thời gian đều làm xuất hiện một từ trường H.
DdS q dV
(5.25)
S V
trong đó thể tích V được bao bởi S.
Công thức (5.25) phát biểu:
Điện thông gửi qua một mặt kín S bất kỳ bằng tổng đại số các điện tích nằm trong mặt kín đó.
5.3.3. Hệ cặp phương trình Maxwell dưới dạng vi phân
a. Cặp phương trình Maxwell thứ nhất
Các phương trình (5.22) đến (5.25) được viết dưới dạng tích phân, trong
đó các đại lượng
E, B, D, H
lần lượt là vectơ cường độ điện trường, vectơ cảm
ứng từ và vectơ điện cảm tại các điểm khác nhau của trường. Nhưng, để tính các đại lượng nói trên tại cùng một điểm của trường, chúng ta cần phải áp dụng phương trình Maxwell cho những diện tích vô cùng nhỏ. Nói một cách khác chúng ta phải viết các phương trình Maxwell dưới dạng vi phân.
Áp dụng định lý Stokes cho vế trái của phương trình (5.22), ta có :
Edl rotEdS
(5.26)
C S
trong đó S là diện tích bao bởi đường cong l. Từ phương trình (5.22), ta viết được:
B
rotEdS t dS
(5.27)
S S
Từ đó suy ra:
B
(5.28)
rotE t
Phương trình phương (5.28) là phương trình thứ nhất của cặp phương trình Maxwell thứ nhất. Đó là biểu thức toán học nêu lên điện trường có tính chất xoáy.
Áp dụng định lý Oxtrogradxki - Gaux ta có:
BdS divBdV
S
(5.29)
trong đó V là thể tích bị bao bởi mặt S. Dựa vào (5.29) ta viết được:
divB dV 0 (5.30)
Vì thể tích V là tùy ý, do đó:
divB 0 (5.31)
Ta thu được phương trình thứ hai (5.31) của cặp phương trình Maxwell thứ nhất. Đó là một biểu thức toán học nói lên từ trường không có nguồn, trong tự nhiên không có từ tích .
b. Cặp phương trình Maxwell thứ hai
Áp dụng định lý Stokes, vế trái của phương trình (5.24) có thể viết thành:
H dl
C
rotH dS
S
(5.32)
trong đó S là mặt giới hạn bởi đường cong kín l. Dựa vào phương trình (5.22) ta có:
H dl
rotH dS
D
(5.33)
C S
Từ đó, ta rút ra:
D
(Jdan
S
t )dS
(5.34)
rotH
Jdan t
Đó là phương trình thứ nhất của cặp phương trình Maxwell thứ hai.
Áp dụng định lý Oxtrogradxki - Gaux cho vế trái của phương trình (5.25) ta có :
DdS divDdV
(5.35)
S V
Phương trình (5.37) và (5.27) cho ta:
divD.dV dV
(5.36)
V V
Ta có:
divD (5.37)
Ta thu được phương trình thứ hai của cặp phương trình Maxwell thứ hai.
Đó là một biểu thức toán học nói lên điện trường có nguồn.
5.4. SÓNG ĐIỆN TỪ
5.4.1. Sự tạo thành sóng điện từ
Vào những năm 1887 – 1889, Heirich Hertz đã kiểm tra và xác nhận bằng thực nghiệm lý thuyết điện từ của Maxwell. Ông nhận thấy các sóng điện từ có thể phản xạ, khúc xạ, hội tụ hoàn toàn như Maxwell đã tiên đoán trên cơ sở hệ phương trình trường điên từ của mình từ những năm 1864 - 1873.
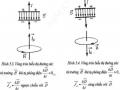
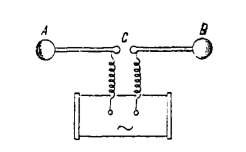
Trong thí nghiệm của mình, Hertz dùng một nguồn điện xoay chiều cao tần nối qua hai ống dây tự cảm đến hai thanh kim loại ở đầu có gắn hai quả cầu kim loại A và B (Hình
5.5). Điều chỉnh khoảng cách AB để có hiện
Hình 5.5
tượng phóng điện qua AB. Khi đó, giữa AB đã xuất hiện một điện trường biến thiên theo thời gian. Thí nghiệm của Hertz đã xác nhận có trường điện từ biến thiên lan truyền trong không gian. Quá trình này được giải thích dựa vào hai luận điểm của Maxwell.
Giả sử tại một điểm nào đó ta tao ra một điện trường biến thiên theo thời gian t. Theo luận điểm thứ hai của Maxwell điện trường biến thiên này sẽ làm
xuất hiện từ trường biến thiên tại các điểm lân cận. Các từ trường biến thiên này, đến lượt mình, lại tạo ra các điện trường biến thiên phù hợp với luận
điểm thứ nhất của Maxwell. Cứ như thế, từng cặp E , B … hợp nhất tạo thành trường điện từ lan truyền trong không gian dưới dạng sóng, gọi là sóng điện từ.
5.4.2. Phương trình sóng điện từ
Xét môi trường truyền sóng điện từ là chân không hoặc điện môi. Như vậy trong môi trường không có điện tích tự do và không có dòng điện ( 0 , j=0), hệ phương trình (5.28), (5.29), (5.34), (5.37) bây giờ trở thành :
B
(5.38)
rotE t
divB 0
(5.39)
D
(5.40)
rotH t
divD (5.41)
Hệ các phương trình trên vẫn có nghiệm, nghĩa là vẫn tồn tại B và D ngay khi và j bằng không. Điều đó chứng tỏ, trường điện từ vẫn tồn tại không cần có dòng điện và điện tích duy trì nó. Trường điện lừ lan truyền trong chân không tạo thành sóng điện từ. Trường điện từ là một dạng đặc biệt của vật chất. Nó có mang năng lượng, bằng thực nghiệm ta đã thu được năng lượng đó trong sóng điện từ. Như vậy, năng lượng điện từ định xứ ở trong trường, chứ không định xứ trên dòng điện hay điện tích gây ra trường đó.
Để tìm phương trình của sóng điện từ, trước hết ta chú ý rằng các trường
E và B nhất thiết phải là các trường biến thiên, vì nếu không ta sẽ có
B 0, D 0 như vậy hệ các phương trình trên sẽ cho ta có trường không đổi,
t t
cụ thể là trường tĩnh điện D và từ trường không đổi H nhưng 0 và j 0
nên khi đó các trường này cũng bằng không.
Bằng phép tính toán học ta chứng minh được phương trình sóng điện từ có dạng:
2 E 1
v2
2 E
2t 0
(5.42)
Đó là phương trình truyền sóng của điện trường E với tốc độ truyền
00
v 1
. Tương tự, ta cũng thu được phương trình cho B
2 B 1
v2
Phép tính chứng tỏ:
2 B
2t 0
(5.43)
0 o
1 3.108 m / s
Vậy
v c
(5.44)
trong đó c là vận tốc ánh sáng trong chân không.
Trừ các chất sắt từ còn tất cả các vật liệu đều có 1. Do đó vận tốc truyền sóng điện từ trong các chất điện môi có dạng v c
Trong chân không 1, 1, do đó v=c.
Vậy: trong chân không sóng điện từ lan truyền với vận tốc bằng vận tốc ánh sáng trong chân không.
Đặt: n gọi là chiết suất tuyệt đối của môi trường.
Vì và đều không nhỏ hơn đơn vị, do đó v c , có nghĩa là vận tốc sóng điện từ trong chân không có giá trị lớn nhất so với trong các môi trường khác.
5.4.3. Sóng điện từ đơn sắc phẳng
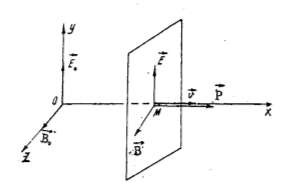
Ta xét một trường hợp riêng của các sóng điện từ, trong đó trường chỉ phụ thuộc vào một toạ độ, tọa độ x chẳng hạn (và thời gian). Đó là các sóng phẳng, xuất hiện khi nguồn ở rất xa phát các sóng với một tần số xác định. Các mặt sóng là những mặt phẳng. Trong sóng điện từ phẳng đơn sắc vectơ E và B vuông góc với phương truyền sóng x. B vuông góc với phương truyền x trong sóng điện từ phẳng. Vậy sóng
điện từ phẳng là sóng ngang vì trong đó các vectơ dao động E và B vuông góc với phương truyền sóng. Gọi n là vectơ đơn vị nằm theo phương truyền sóng.
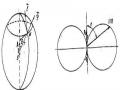
Dựa vào phương trình Maxwell, ta có thể chứng minh được:
Hình 5.6
c
1
B n, E(5.45)
Phương trình (5.45) chứng tỏ sóng điện từ phẳng là sóng ngang. Các vectơ dao động E và B vuông góc với phương truyền sóng, ngoài ra E và B vuông góc với nhau. Ba vectơ E , B , n lập thành một tam diện thuận (Hình
5.6).
Phép tính chứng tỏ E và B luôn luôn dao động cùng pha, trị số của chúng tỷ lệ với nhau Hình 5.7:
0 E
0 H
(5.46)