Những Phát Biểu Tương Đương Của Định Luật Descartes

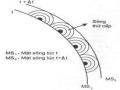
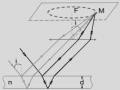
Các ảo ảnh quan sát được trong các vùng sa mạc hay đồng cỏ cũng được giải thích dựa trên hiện tượng khúc xạ và phản xạ toàn phần Hình l.4. Nhờ sự uốn cong của tia sáng nên một số vật ở khuất xa dưới đường chân trời

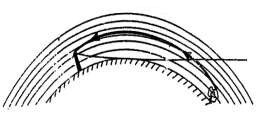
Hình1.4. Sự tạo thành ảo ảnh

sẽ được nhìn thấy và hình như ở gần người quan sát hơn.

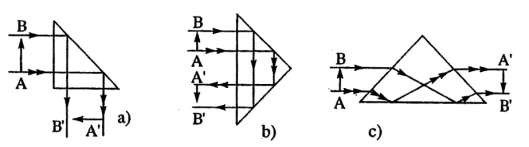
Hình 1.5. Các lăng kính phản xạ toàn phần

Có thể bạn quan tâm!

• Trường Điện Từ Và Hệ Phương Trình Maxwell
• Các Phương Trình Của Trường Điện Từ (Hệ Phương Trình Maxwell):
• Định Luật Về Tác Dụng Độc Lập Của Các Tia Sáng
• Các Đại Lượng Trắc Quang Là Các Đại Lượng Dùng Trong Kĩ Thuật Đo Lường Ánh Sáng.
• Gương Fresnel Hình 2.10. Lưỡng Thấu Kính Bile
• Giao Thoa Gây Bởi Bản Mỏng Có Bề Dày Không Đổi. Vân Cùng Độ Nghiêng

Xem toàn bộ 258 trang tài liệu này.

Hiện tượng phản xạ toàn phần được ứng dụng để đổi chiều tia sáng trong các dụng cụ quang học. Chiết suất của nhiều loại thuỷ tinh vào cỡ 1,5. Vì vậy góc tới giới hạn trên biên giới thuỷ tinh không khí cỡ 420 và khi góc tới bằng 450 sẽ luôn luôn xảy ra hiện tượng phản xạ toàn phần.

Hình 1.5 biểu diễn các lăng kính phản xạ toàn phần. Trong trường hợp

(a) ảnh và phương truyền của ánh sáng bị quay đi một góc 900 do phản xạ toàn phần tại mặt đáy của lăng kính. Trong trường hợp bị ảnh và phương truyền của ánh sáng bị đổi chiều do hai lần phản xạ toàn phần trên hai mặt bên của lăng kính.

Trong trường hợp b) ảnh và phương truyền của ánh sáng bị đổi chiều do hai lần phản xạ toàn phần trên hai mặt bên của lăng kính.

Trong trường hợp c) ảnh cũng bị đổi chiều do phản xạ toàn phần ở mặt đáy của lăng kính nhưng chiều truyền của ánh sáng lại không đổi.

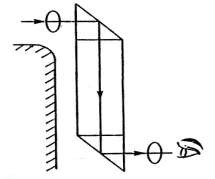
Hình 1.6 biểu diễn sơ đồ của một loại ống nhòm dùng quan sát những vật bị che khuất, về nguyên tắc có thể dùng hai gương phẳng đặt nghiêng 450 để thay các lăng kính phản xạ toàn phần.

Tuy nhiên khi phản xạ từ gương kim loại một phần ánh sáng xuyên vào kim loại và bị hấp thụ trong đó. Khi dùng lăng kính phản xạ toàn phần sự mất mát đó không xảy ra. Ngày nay hiện tượng phản xạ toàn phần còn

được ứng dụng trong sợi cáp quang.

1.2. NHỮNG PHÁT BIỂU TƯƠNG ĐƯƠNG CỦA ĐỊNH LUẬT DESCARTES

Hình 1.6. Ống nhòm quan sát các vật bị che khuất

1.2.1. Quang lộ

Xét hai điểm A, B trong một môi trường đồng tính chiết suất n, cách

nhau một đoan bằng d.

Thời gian ánh sáng đi từ A đến B là t d , trong đó v là vận tốc ánh sáng

v

trong môi trường.

Điṇ h nghia quang lộ:

Quang lộ giữa hai điểm A, B là đoan

đườ ng ánh sáng truyền đươc

trong

chân không vớ i cùng khoảng thờ i gian t cần thiết để sóng ánh sáng đi đươc

đoan

đườ ng d trong môi trườ ng chiết suất n.

L c.t c. d nd (1.7)

v

trong đó: n là chiết suất c ủa môi trường n c v , c là vận tốc ánh sáng trong chân không.

Như v ậy khi ánh sáng truyền trong môi trường chất , với vi ệc sử dung

khái niệm quang lộ chúng ta đã chuyển quãng đường á nh sáng đi đươc

trong

môi trường chiết suất n sang quãng đường tương ứ ng trong chân không và do

đó ta có thể sử dung v ận tốc truyêǹ của ánh sáng trong chân không là c thay

cho vận tốc v truyền trong môi trường.

Nếu ánh sáng truyền qua nhiều môi trường chiết suất n1, n2, n3 ... với các quãng đường tương ứ ng d1, d2, d3 ... thì quang lộ sẽ là:

L nidi(1.8)

i

Nếu ánh sáng truyền trong môi trường mà chiết suất thay đổi liên tuc

thì

ta chia đoan

đường AB thành các đoan

nhỏ ds để coi chiết suất n không thay

đổi trên mỗi đoan

nhỏ đó và quang lộ sẽ là:

B

L n ds

A

(1.9)

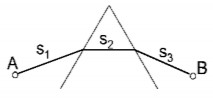
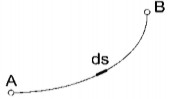
Hình 1.7

1.2.2. Nguyên lí Fermat

a. Phát biểu

Giữa hai điểm A, B ánh sáng sẽ truyền theo con đường nào mà quang lộ là cực trị (cực đại, cực tiểu hoặc không đổi).

Hay giữa hai điểm A, B ánh sáng sẽ truyền theo con đường nào hoặc nếu ít thời gian nhất, hoặc mất nhiều thời gian nhất, hoặc sẽ truyền theo những con đường mà thời gian truyền bằng nhau.

b. Sự tương đương giữa nguyên lí Fecmat và các định luật Descartes

Nguyên lí Fermat là một dạng phát biểu tương đương của định luật Descartes. Ta hãy xét sự tương đương này.

Sự tương đương của nguyên lí Fecmat với định luật phản xạ.

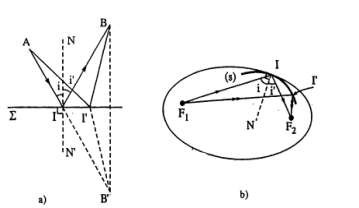
Xét hai điểm A, B nằm phía trên mặt phản xạ. Gọi AIB là con đường ánh sáng truyền từ A đến B. Căn cứ vào định luật phản xạ thì: il = i’1

Xét một điểm I' bất kì trên mặt Σ; gọi B’ là điểm đối xứng của B qua mặt phản xạ thì IB = IB’ và I'B = IB’. Vì ba điểm AIB thẳng hàng ta rút ra:

AI + IB < AI + IB (1.10)

Nhân hai vế với chiết suất n của môi trường, ta có:

LAIB < LAI’B (1.11)

nghĩa là ánh sáng truyền theo con đường mà quang lộ cực tiểu.

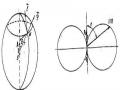
Ta lại xét một mặt elipxôit tròn xoay quanh trục F1F2 có phía trong phản xạ ánh sáng, và

có hai tiêu điểm F1F2 (Hình l.8b). Lấy một điểm I bất kì trên mặt elipxôit, căn cứ vào tính chất của

Hình 1.8. Sự tương đương giữa nguyên lí Fecma và định luật phản xạ

elipxôit, các đoạn thẳng F1 và F2 sẽ hợp với pháp tuyến là những góc bằng nhau. Nếu đặt một nguồn sáng tại Fl thì căn cứ vào định luật phản xạ các tia sáng sau khi đập lên mặt elipxôit đều tập trung tại F2. Mặt khác, ta lại biết rằng elipxôit chính là quỹ tích những điểm có tồng khoảng cách tới hai điểm F1F2 là một độ dài không đồi. Do đó trong trường hợp này, quang lộ của các tia sáng từ F1 tới mặt elipxôit rồi phản xạ về F2 bằng nhau.

Nếu lại xét một mặt nằm phía trong và tiếp xúc với mặt elipxôit tại I (Hình l.8b) thì đối với các mặt đó, chỉ có tại I, góc tới mới bằng góc phản xạ. Căn cứ theo định luật Descartes, ánh sáng chỉ cố thể đi theo con đường F1F2 . So với các con đường khác thì con đường F1F2 ứng với quang lộ cực đại.

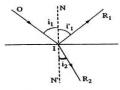
Sự tương đương của nguyên lí Fecmat tới định luật khúc xạ

Xét hai điểm A, B nằm trong hai môi trường có chiết suất n1 và n2.

Lấy một điểm I bất kì trên mặt phân cách, quang lộ theo con đường AIB

là:

L = n1AI + n2IB (1.12)

Gọi: AA' =h1; BB' =h2; A’I=x, A’B’=p,

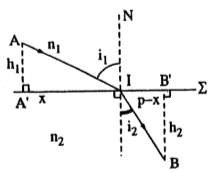
Ta có:

x2 h2

1

L n1

n21

(1.13)

( p x)2h2

2

Theo nguyên lí Fecmat, ánh sáng đi từ A đến B theo con đường mà quang lộ cực trị. Điều đó có nghĩa là ánh sáng sẽ đi theo con đường AIB mà đoạn AI=x thoả mãn điều kiện

dL= 0. Dựa vào (l.13) ta suy ra:

dx

Hình 1.9. Sự tương đương giữa nguyên lí Fecma và định luật khúc xạ

dL n

x n

p x

 0 (1.14)

x2 h2

1

( p x)2h2

2

dx 1 2

Từ (1.14) ta rút ra:

n1.sini1 = n2.sini2 (1.15)

Như vậy xuất phát từ định luật Descartes ta có thể tìm được nguyên lí Fecmat và ngược lại. Rò ràng chúng tương đương với nhau.

1.2.3. Định lí Malus

Ta xét một phát biểu tương đương nữa của các định luật Descartes.

a. Khái niệm mặt trực giao

Mặt trực giao là mặt vuông góc với các tia của một chùm sáng.

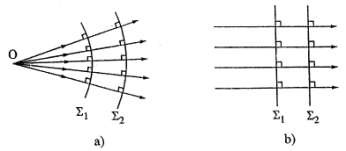
Nếu chùm sáng là chùm đồng quy thì những mặt trực giao là những mặt cầu đồng tâm mà tâm là điểm đồng quy đó; nếu là chùm song song thì những mặt trực giao là những mặt phẳng song song (Hình 1.10).

b. Định lí Maluyt

Quang lộ của các tia sáng giữa hai mặt trục giao của một chùm sáng thì bằng nhau.

Xuất phát từ định luật Đề các, ta hãy chứng minh

định lí Maluyt trong một trường hợp đơn giản.

Hình1.10. Mặt trực giao

Xét một chùm sáng song song truyền qua mặt phân cách hai môi trường trong suất có chiết suất là n1 và n2 (Hình l.11), Σ1, Σ2 là hai mặt trực giao. Ta kẻ I1H2 vuông góc với A2I2 và I2H1 vuông góc với I1Bl.

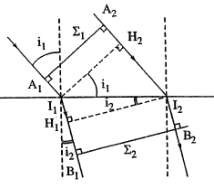
Hình 1.11. Chứng minh định lí Maluyt

Gọi L1 là quang lộ dọc theo con đường A1I1B1 và L2 là quang lộ dọc theo con đường A2I2B2

Ta có: L1 n1.A1I1 n2.I1B1

L1 n1.A1I1 n2.I1H1 n2.H1B1 (l .16)

L2 n1.A2 I2 n2.I2 B2

L2 n1.A2 H2 n1.H2 I2 n2.I2 B2 (l.17)

A1I1 A2 H2, H1B1 I2 B2 A1I1 (l.18)

Mặt khác theo định luật khúc xạ:

n1.sinil =n2.sini2

1

2

n . H2 I2 n . I1H1

(1.19)

I1I2 I1I2

n1.H2I2 =n2.IlHl

Kết quả Ll =L2 nghĩa là quang lộ giữa hai mặt trực giao thì bằng nhau.

1.3. CÁC ĐẠI LƯỢNG TRẮC QUANG

Các đại lượng trắc quang là cáo đại lượng dùng trong kĩ thuật đo lường ánh sáng. Sau đây ta sẽ nghiên cứu một số các đại lượng đó.

1.3.1. Quang thông

Ta đã biết các ánh sáng đơn sắc có bước sóng từ 0,4 m đến 0,76 m khi tác dụng vào mắt sẽ gây ra cảm giác sáng. Tuy nhiên mức độ nhậy cảm của mắt đối với các ánh sáng đơn sắc khác nhau cũng khác nhau. Để đặc trưng cho phần năng lượng gây ra cảm giác sáng người ta đưa ra khái niệm quang thông:

Quang thông do một chùm sáng gửi tới diện tích dS là một đại lượng có trị số bằng phần năng lượng gây ra cảm giác sáng gửi tới dS trong một đơn vị thời gian.

Ngoài quang thông gửi tới diện tích dS, người ta còn định nghĩa quang thông toàn phần của một nguồn sáng. Đó là phần năng lượng gây ra cảm giác sáng do nguồn phát ra theo mọi phương trong một đơn vị thời gian.

1.3.2. Độ sáng

a. Góc khối

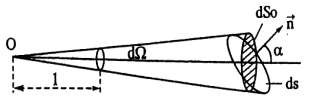
Góc khối nhìn thấy diện tích dS từ điển O là phần không gian giới hạn bởi hình nón có đỉnh tại O và có các đường sinh tựa trên chu vi của dS.

Theo hệ SI và bảng đơn vị hợp pháp, đơn vị góc khối là stêrađian (viết tắt là sr). Như vậy góc khối

toàn phần sẽ là 4π stêrađian.

Ta tìm liên hệ giữa góc khối

Hình 1.12. Góc khối

dvà diện tích dS. Vẽ mặt cầu tâm O và bán kính bằng đơn vị (Hình l.12). Giá trị của góc khối được đúng hàng phần diện tích mặt cầu giới hạn trong hình nón. Gọi r là khoảng cách từ O đến dS, a là góc giữa pháp tuyến n của dS và r, dSo là hình chiếu của dS lên mặt phẳng vuông góc với r, ta có:

d1 2



(1.20)

dS0 r 

Biết dSo=ds.cosα, ta rút ra:

ddS.cos

r 2

(1.21)

b. Độ sáng

Đó là đại lượng đặc trưng cho khả năng phát sáng của nguồn theo một phương. Theo định nghĩa, độ sáng của nguồn theo một phương nào đó là một đại lượng có trị số bằng quang thông của nguồn gửi đi trong một đơn vị góc khối theo phương đó.

Gọi I là độ sáng, dlà quang thông gửi đi trong góc khối dΩ, ta có:

I d

d

(l.22)

Độ sáng I của nguồn thay đổi theo phương phát sáng. Nếu độ sáng I

theo mọi phương đều như nhau thì nguồn gọi là nguồn đẳng hướng.