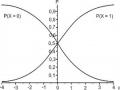
thừa dạng hàm hợp. Tập xác định của hàm số hợp của hàm số lũy thữa | ||
Vận dụng: Phương trình , bất phương trình ,hệ phương trình mũ chứa tham số, Phương trình, bất phương trình , hệ phương trình lôgarit chứa tham số | ||
Vận dụng cao: Sử dụng công thức mũ,logarit, tính chất hàm số mũ, logarit trong các bài toán về tính chất , giá trị lớn nhất , nhỏ nhất của hàm số hợp của hàm số mũ, hàm số logarit, Phương trình mũ phức tạp, các ứng dụng thực tế | ||
3. Nguyên hàm - tích phân và ứng dụng (7 câu) | Nhận biết: Tìm họ nguyên hàm dựa vào bảng nguyên hàm | |
Nhận biết : Tìm họ nguyên hàm của hàm số dựa vào bảng nguyên hàm, tính chất nguyên hàm | ||
Thông hiểu: Tính tích phân của hàm số | ||
Thông hiểu: Tìm một nguyên hàm của hàm số có điều kiện | ||
Thông hiểu: Sử dụng tìm nguyên hàm với các câu hỏi khác | ||
Vận dụng: Tính tích phân , ứng dụng của tích phân | ||
Vận dụng cao: Sử dụng tìm nguyên hàm, tính tích phân của hàm số với các bài toán liên quan khác. Ứng dụng vào bài toán thực tế | ||
4. Số phức (6 câu) | Nhận biết: Xác định các tham số cơ bản của số phức | |
Nhận biết: Các phép toán cơ bản với số phức | ||
Nhận biết: Các dạng biểu diễn của số phức | ||
Thông hiểu: Nghiệm phương trình bậc nhất, bậc hai hệ số thực của số phức. |
Có thể bạn quan tâm!
-
 Về Trắc Nghiệm Đa Phân Và Trắc Nghiệm Đa Chiều
Về Trắc Nghiệm Đa Phân Và Trắc Nghiệm Đa Chiều -
 Dữ Liệu Tính Toán Ước Lượng Hàm Đặc Trưng Câu Hỏi
Dữ Liệu Tính Toán Ước Lượng Hàm Đặc Trưng Câu Hỏi -
 Qui Trình Xây Dựng Ngân Hàng Câu Hỏi Trắc Nghiệm Khách Quan
Qui Trình Xây Dựng Ngân Hàng Câu Hỏi Trắc Nghiệm Khách Quan -
 Phân Tích Câu Hỏi Thi Bằng Lý Thuyết Khảo Thí Hiện Đại
Phân Tích Câu Hỏi Thi Bằng Lý Thuyết Khảo Thí Hiện Đại -
 Bản Đồ Phân Bố Độ Khó Câu Hỏi Thi Và Năng Lực Thí Sinh
Bản Đồ Phân Bố Độ Khó Câu Hỏi Thi Và Năng Lực Thí Sinh -
 Phân Tích Đa Chiều Năng Lực Của Ts Với Đề Thi 01.
Phân Tích Đa Chiều Năng Lực Của Ts Với Đề Thi 01.
Xem toàn bộ 137 trang tài liệu này.
Thông hiểu: Các bài toán liên quan đến môđun, đến tính toán biểu thức phức | ||
Vận dụng: Các tính toán phức tạp, các bài toán hình học liên quan đến mô đun số phức. | ||
5. Thể tích khối đa diện (5 câu) | Nhận biết: Thể tích khối chóp dễ xác định đường cao, diện tích đáy. Thể tích khối lăng trụ đứng dễ xác định đường cao, diện tích đáy | |
Thông hiểu: Tính thể tích khối chóp có liên quan đến yếu tố cạnh hoặc góc đơn giản . Tính thể tích khối lăng trụ đứng có liên quan đến yếu tố cạnh hoặc góc đơn giản | ||
Thông hiểu: Các khái niệm liên quan đến khối đa diện: Mặt, cạnh, đỉnh, mặt đối xứng,…, đa diện đều. | ||
Vận dụng: Tính thể tích khối chóp có sử dụng kiến thức ở mức độ cao hơn về quan hệ vuông góc, góc, khoảng cách để xác định đường cao, diện tích đáy. Tính thể tích khối lăng trụ có sử dụng kiến thức ở mức độ cao hơn về quan hệ vuông góc, góc, khoảng cách để xác định đường cao, diện tích đáy. Tính thể tích khối lăng trụ, khối hộp xiên | ||
Vận dụng cao: Tính thể tích khối chóp không xác định trực tiếp phải sử dụng thông qua tỉ số thể tích, phân chia khối đa diện. Cực trị khối đa diện. | ||
6. Khối tròn xoay (3 câu) | Nhận biết: Công thức thể tích, diện tích liên quan đến khối nón, khối trụ, khối cầu. | |
Thông hiểu: Khối nón có liên quan thiết diện. Khối trụ có liên quan thiết diện | ||
Vận dụng: Xác định tâm và tính bán kính mặt cầu ngoại tiếp |
khối chóp. Nón, trụ có liên quan đến góc, khoảng cách, thiết diện. Thể tích khối trụ, diện tích xung quanh ,diện tích toàn phần hình trụ- Bài toán thực tế. | ||
7. Phương pháp tọa độ trong không gian (8 câu) | Nhận biết: Các phép toán về véc tơ, điểm. | |
Nhận biết: Viết, xác định phương trình mặt phẳng khi biết một điểm và một vec tơ pháp tuyến | ||
Nhận biết: Viết, xác định phương trình đường thẳng khi biết một điểm và một vectơ chỉ phương | ||
Nhận biết: Viết phương trình mặt cầu khi biết tâm và bán kính. | ||
Thông hiểu: Các bài toán viết phương trình mặt phẳng, đường thẳng cần xác định được vectơ pháp tuyến hay chỉ phương liên quan điểm các đường thẳng, mặt phẳng đặc biệt.(hình chiếu, khoảng cách từ điểm lên các trục Ox, hay mặt phẳng (Oxy) | ||
Thông hiểu: Các bài toán liên quan đến tương giao, hình chiếu, khoảng cách của điểm, đường thẳng, mặt phẳng. | ||
Vận dụng: Các bài toán tìm điểm trên mặt phẳng, đường thẳng,… thỏa mãn các điều kiện cho trước. | ||
Vận dụng cao: Ứng dụng hình giải tích vào hình không gian hoặc xử lý các bài toán cực trị hình học liên quan đến véc tơ, điểm, mặt phẳng, mặt cầu, đường thẳng. |
2.3.3. Biên soạn câu hỏi thi
Để biên soạn câu hỏi thi ta làm theo quy trình sau:
Bảng 2.4. Quy trình biên soạn câu hỏi thi
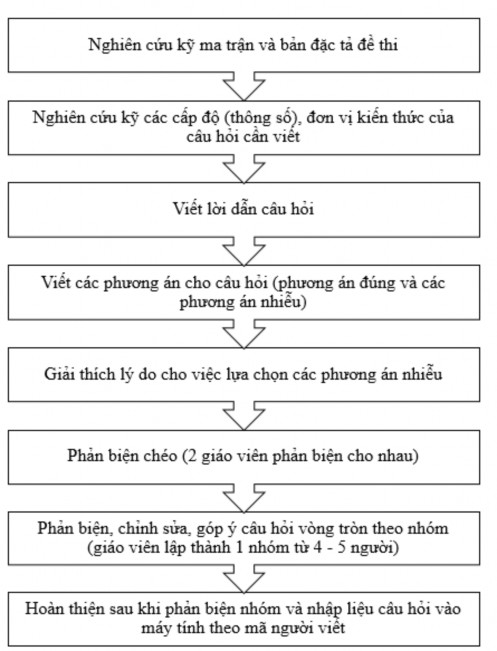
Ta xây dựng từng câu hỏi thi theo quy ước đánh mã từ 1 – 50 cho các loại câu hỏi thi. Khi đó ta biên soạn từng mã câu hỏi thi như sau:
Mã số 1. KH: HS.A1.STT ( Câu hỏi hàm số mức độ dễ (A) loại 1 gắn với số thứ tự của câu hỏi.
y ax b
Yêu cầu: Nhận biết: Nhận biết đồ thị của hàm số bậc ba, bậc 4 trùng phương , hàm số cx d , tương giao giữa các đồ thị đơn giản.
Bảng 2.5. Bảng xây dựng câu hỏi thi
Nội dung | Đáp án | Nhiễu 1 | Nhiễu 2 | Nhiễu 3 | Ghi chú | |
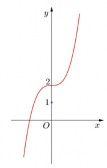
HS.A1.1 | Đường cong trong hình bên là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D. Hỏi hàm số đó là hàm số nào ? | y x3 2. | y x2 1. | y x4 2. | y x3 1. | Chú ý: Các lỗi, bẫy học sinh |
HS.A1.2 | Hình bên là đồ thị của hàm số nào dưới đây ? | y x3 3x 1. | y x3 3x 1. | y x2 3x 1. | y x4 3x2 1. |
68
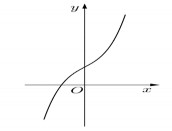
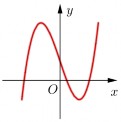
Đường cong dưới đây là đồ thị của hàm số nào ? | y x3 x 1. | y x4 1. | y x3 x 2 | y x3 2x 3. | ||
HS.A1.4 | Đồ thị của hàm số y x4 2x2 3 và đồ thị của hàm số y 2x3 x2 2x 3 có bao nhiêu điểm chung ? | Bốn. | Một. | Hai. | Ba. | |
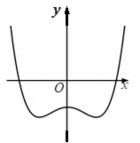
HS.A1.5 | Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ? | y x4 x2 1 | y x3 x2 1 | y x3 x2 1 | y x4 x2 1 |
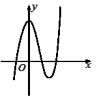
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào ? | y x3 3x2 3 | y x4 2x2 1 | y x4 2x2 1 | y x3 3x2 1 | ||
HS.A1.7 | Cho hàm số y (x 2)(x2 1) có đồ thị (C). Mệnh đề nào dưới đây đúng ? | (C) cắt trục hoành tại một điểm. | (C) cắt trục hoành tại hai điểm | (C) cắt trục hoành tại ba điểm. | (C) không cắt trục hoành. |
…