CAU_16 | -0.228 | 0.245 | 1.08 ( 0.60, 1.40) 0.4 | 0.94 ( 0.64, 1.36) -0.3 | |
17 | CAU_17 | -1.225 | 0.272 | 0.46 ( 0.61, 1.39) -3.3 | 0.79 ( 0.39, 1.61) -0.7 |
18 | CAU_18 | -0.170 | 0.242 | 0.73 ( 0.61, 1.39) -1.4 | 0.80 ( 0.66, 1.34) -1.2 |
19 | CAU_19 | -0.556 | 0.252 | 0.79 ( 0.61, 1.39) -1.0 | 0.88 ( 0.58, 1.42) -0.5 |
20 | CAU_20 | 0.948 | 0.227 | 1.14 ( 0.61, 1.39) 0.8 | 1.11 ( 0.79, 1.21) 1.0 |
21 | CAU_21 | 1.916 | 0.237 | 1.56 ( 0.60, 1.40) 2.4 | 1.30 ( 0.74, 1.26) 2.1 |
22 | CAU_22 | -0.702 | 0.256 | 0.91 ( 0.61, 1.39) -0.4 | 0.95 ( 0.55, 1.45) -0.2 |
23 | CAU_23 | 0.373 | 0.232 | 0.90 ( 0.61, 1.39) -0.4 | 0.93 ( 0.74, 1.26) -0.5 |
24 | CAU_24 | 0.570 | 0.230 | 1.07 ( 0.61, 1.39) 0.4 | 1.09 ( 0.76, 1.24) 0.8 |
25 | CAU_25 | -0.843 | 0.261 | 0.43 ( 0.60, 1.40) -3.5 | 0.67 ( 0.51, 1.49) -1.4 |
26 | CAU_26 | -0.860 | 0.261 | 1.07 ( 0.61, 1.39) 0.4 | 0.89 ( 0.51, 1.49) -0.4 |
27 | CAU_27 | 1.717 | 0.237 | 1.18 ( 0.59, 1.41) 0.9 | 1.03 ( 0.76, 1.24) 0.3 |
28 | CAU_28 | 1.226 | 0.227 | 0.92 ( 0.61, 1.39) -0.4 | 0.94 ( 0.80, 1.20) -0.6 |
29 | CAU_29 | -2.474 | 0.308 | 0.61 ( 0.61, 1.39) -2.2 | 0.98 ( 0.00, 2.22) 0.2 |
30 | CAU_30 | -3.216 | 0.322 | 0.51 ( 0.61, 1.39) -3.0 | 0.98 ( 0.00, 2.83) 0.3 |
31 | CAU_31 | -2.503 | 0.309 | 0.38 ( 0.61, 1.39) -4.1 | 0.92 ( 0.00, 2.24) 0.1 |
32 | CAU_32 | -0.568 | 0.252 | 0.83 ( 0.61, 1.39) -0.9 | 0.88 ( 0.58, 1.42) -0.5 |
33 | CAU_33 | 0.262 | 0.234 | 0.99 ( 0.61, 1.39) 0.0 | 1.03 ( 0.73, 1.27) 0.2 |
34 | CAU_34 | 0.522 | 0.233 | 1.03 ( 0.60, 1.40) 0.2 | 1.01 ( 0.75, 1.25) 0.1 |
35 | CAU_35 | 0.752 | 0.228 | 0.82 ( 0.61, 1.39) -0.9 | 0.85 ( 0.78, 1.22) -1.3 |
36 | CAU_36 | 2.239 | 0.244 | 1.14 ( 0.60, 1.40) 0.7 | 1.08 ( 0.68, 1.32) 0.5 |
37 | CAU_37 | -0.064 | 0.240 | 1.37 ( 0.61, 1.39) 1.7 | 1.10 ( 0.68, 1.32) 0.7 |
38 | CAU_38 | 1.634 | 0.235 | 1.03 ( 0.59, 1.41) 0.2 | 1.00 ( 0.77, 1.23) 0.0 |
39 | CAU_39 | 2.727 | 0.260 | 1.86 ( 0.59, 1.41) 3.4 | 1.18 ( 0.54, 1.46) 0.8 |
40 | CAU_40 | -0.304 | 0.245 | 0.72 ( 0.61, 1.39) -1.5 | 0.80 ( 0.63, 1.37) -1.1 |
41 | CAU_41 | 0.363 | 0.232 | 0.77 ( 0.61, 1.39) -1.2 | 0.82 ( 0.74, 1.26) -1.4 |
42 | CAU_42 | 1.092 | 0.235 | 1.39 ( 0.58, 1.42) 1.7 | 1.27 ( 0.79, 1.21) 2.3 |
43 | CAU_43 | -2.064 | 0.297 | 0.47 ( 0.61, 1.39) -3.3 | 0.89 ( 0.03, 1.97) -0.1 |
44 | CAU_44 | -2.063 | 0.297 | 0.66 ( 0.61, 1.39) -1.8 | 0.97 ( 0.03, 1.97) 0.1 |
45 | CAU_45 | -0.433 | 0.249 | 0.71 ( 0.61, 1.39) -1.5 | 0.87 ( 0.61, 1.39) -0.6 |
46 | CAU_46 | -0.432 | 0.249 | 0.78 ( 0.61, 1.39) -1.1 | 0.79 ( 0.61, 1.39) -1.1 |
47 | CAU_47 | 0.364 | 0.232 | 0.95 ( 0.61, 1.39) -0.2 | 0.97 ( 0.74, 1.26) -0.2 |
48 | CAU_48 | 2.986 | 0.265 | 0.92 ( 0.60, 1.40) -0.3 | 0.95 ( 0.47, 1.53) -0.1 |
49 | CAU_49 | 1.908 | 0.237 | 1.23 ( 0.60, 1.40) 1.1 | 1.10 ( 0.74, 1.26) 0.8 |
50 | CAU_50 | 1.728* | 1.781 | 1.26 ( 0.58, 1.42) 1.2 | 1.10 ( 0.76, 1.24) 0.8 |
Có thể bạn quan tâm!
-
Qui Trình Xây Dựng Ngân Hàng Câu Hỏi Trắc Nghiệm Khách Quan -
Triển khai đánh giá kết quả học tập môn Toán lớp 12 bằng một đề tổng hợp với các câu hỏi nhị phân, đa phân và đa chiều - 10 -
Phân Tích Câu Hỏi Thi Bằng Lý Thuyết Khảo Thí Hiện Đại -
Phân Tích Đa Chiều Năng Lực Của Ts Với Đề Thi 01. -
Biểu Đồ Tương Quan Giữa Năng Lực Của Thí Sinh Và Độ Khó Của Đề Thi 02 -
Mẫu Đặc Tả Kiến Thức Môn Toán 12 Theo Chuẩn Kiến Thức Kĩ Năng Bộ Giáo Dục Ban Hành.
Xem toàn bộ 137 trang tài liệu này.
Dựa vào bảng số liệu trong file ex1.shw mà ta thấy các câu hỏi 4, 11, 17, 21, 30, 39 là những câu cần phải loại bỏ vì nó nằm ngoài vùng năng lực của thí sinh (có thể nó quá dễ hoặc quá khó với thí sinh). Hay nói một cách khác câu hỏi thi không tìm được mô hình, hàm đặc trưng. Quá trình ước lượng tham số của câu hỏi không thành công.
Chúng ta xem xét các hàm đặc trưng của các câu hỏi để thấy được việc ước lượng tham số (độ khó) cho các câu hỏi thường khó khăn, trong nhiều trường hợp là không ước lượng được bởi sai số giữa hàm đặc câu hỏi trưng quan sát, và đặc trưng câu hỏi tính toán là quá lớn. Chúng ta xem xét một số câu dự định loại bỏ ở trên.
Câu số 4.
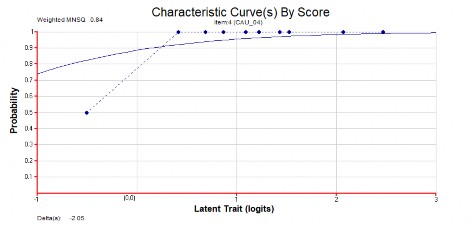
Hình 3.1 Đồ thị hàm đặc trưng câu hỏi số 4.
Câu số 21.
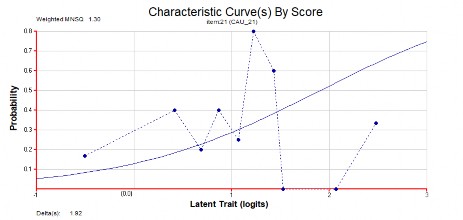
Hình 3.2 Đồ thị hàm đặc trưng câu hỏi số 21.
Câu 39.
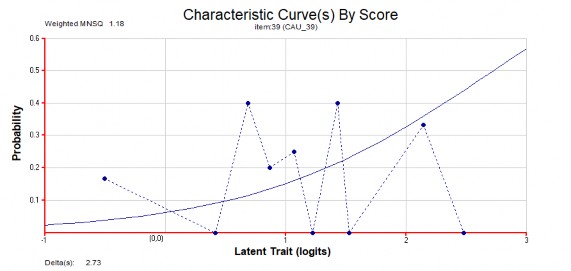
Hình 3.3 Đồ thị hàm đặc trưng câu hỏi số 39.
Các câu 4, 21, 39 ở trên đều là những câu rất khó ước lượng được tham số câu hỏi, bởi các đáp ứng của TS với CH là rời rạc và khó hội tụ. Do vậy hàm đặc trưng câu hỏi không tính được các tham số của câu hỏi (quá trình ước lượng không hội tụ). Nhìn trên các hình vẽ chúng ta thấy đường chấm xanh không bám sát vào các đường liền xanh.
Trong khi đó đường cong quan sát của câu hỏi và đường cong tính toán của câu hỏi 40 là có xu hướng hội tụ.
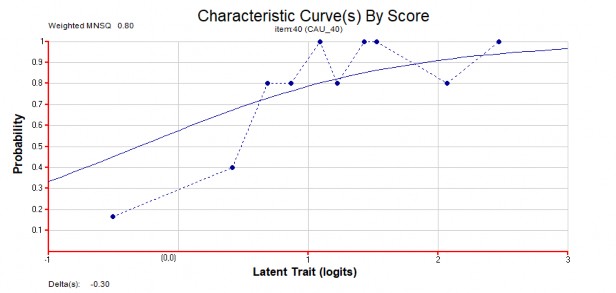
Hình 3.4 Đồ thị hàm đặc trưng câu hỏi số 40.
b) Sơ đồ phân bố độ khó câu hỏi thi và năng lực thí sinh
+item
---------------------------------------------------------------------------------------
| |
| |
| |
4 | |
| |
| |
| |
| |
| |
| |
| |
| |
3 |48 |
XXXX| |
|39 |
XX| |
XX| |
XXXXXXXXX| |
XX| |
XXXXXXXXXXXXXXX|36 |
XXXXX| |
2 XXXXXXXXXXXXXXX| | XXXXXXXXXXXXXXX|21 49 |
XXXXXXXXXXXXXXXXXXXXXXXXXXX|8 27 50 |
XXXXXXXXX|11 38 |
XXXXXXXXXXXXXXXXXXXXXXXXXXX| |
XXXXXXXXXXXXXXXXXXXXXXXXXXXXX| |
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX| |
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX|28 |
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX|42 |
1 XXXXXXXXXXXXXXXXXX|20 |
XXXXXXXXXXXXXXXXXXXXXXXX| |
XXXXXXXXXXXXXXXXXX|5 35 |
XXXXXXXXXXXXXXXX|13 24 |
XXXXXXXXXXXXX|10 34 |
XXXXXXXXXXX|23 41 47 |
XXXXXXXXXXXXX|9 14 33 |
XXXXX| |
0 XXXXXXX| |
XXXXXXXXXXXXXXX|37 |
XXXXX|1 6 18 |
XXXXX|16 40 |
XXXXXXXXXXX|7 45 46 |
XXXXXXXXXXXXX|19 |
XX|32 |
XXXXX|22 |
XXXX|25 26 |
-1 XXXXX| |
| |
|17 |
| |
XX|3 |
| |
| |
| |
| |
-2 |12 15 |
|2 4 43 44 |
| |
|29 30 31 |
=======================================================================================
Each 'X' represents 0.1 cases
Hình 3.5 Bản đồ phân bố độ khó câu hỏi thi và năng lực thí sinh
Bản đồ phân bố độ khó câu hỏi thi và năng lực thí sinh cho thấy mức độ phù hợp của đề thí đối với thí sinh dự thi. Có thể là đề thi quá dễ, quá khó hoặc rất phù hợp. Bản đồ phân bố cho thấy đề thi đo được hầu hết năng lực của thí sinh hay còn có những khoảng trống cần bổ sung một số câu hỏi để đo và phân biệt được năng lực của các thí sinh ở đó. Ở hình minh họa 2.6 đề thi này là dễ so với năng lực của thí sinh. Các câu hỏi ở mức độ trung bình còn ít, cần bổ xung. Các câu hỏi 12, 15, 2, 4, 43, 44, 29, 30, 31 là rất dễ so với năng lực của tập thí sinh đang kiểm tra. Vì vậy ta phải soạn lại các câu hỏi này nhằm tăng độ khó của câu hỏi. Chúng ta hoàn toàn có thể lấy các câu hỏi 12, 15, 2, 4, 43, 44, 29, 30, 31 từ các đề tương đương 02, 03, 04 rồi tính toán lại các tham số đặc trưng (đường cong đặc trưng) của đề thi và hàm thông tin của đề thi.
c) Đường cong đặc trưng của đề thi
Dựa vào kết quả chạy của phần mềm Conquest ta dễ dàng có tham số đặc trưng (độ khó b) của từng câu hỏi. ví dụ từ bảng 2.8 câu hỏi 1 có độ khó b = -0.18
nên hàm đặc trưng của câu hỏi 40 có dạng
b
e
P()
1eb
e0.18
1e0.18
và đồ thị của
nó là hình 2.5. Một cách khác để xác định độ khó của câu hỏi (Item) là dựa vào
đường cong đặc trưng câu hỏi. Nếu
P() 0.5 thì độ khó câu hỏi b .
Để giúp ích cho việc so bằng điểm cũng như chuẩn hóa đề thi, việc tính toán đường cong đặc trưng cho cả đề thi là hết sức cần thiết. Thực ra việc tính toán đường cong đặc trưng cho đề thi là việc cộng gộp tất cả các đường cong đặc trưng của từng câu hỏi thi. Dựa vào đường cong đặc trưng của đề thi, ứng với thi sinh có năng lực làthì ta hoàn toàn có thể ước lượng được điểm của thí sinh đó. Đồng thời dựa vào hàm đặc trưng của đề thi chúng ta sẽ biết đề thi nào khó hoặc dễ hơn với các nhóm học sinh có năng lực khác nhau.
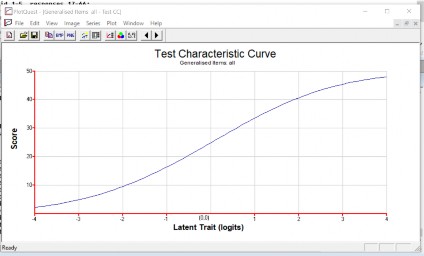
Hình 3.6 Đường cong đặc trưng của đề thi số 1.
Nhận xét: dựa vào đường cong đặc trưng của từng câu hỏi thi chúng ta dễ dàng tính được độ khó, độ phân biệt của các câu hỏi thi, đề thi theo lý thuyết IRT.
d) Hàm thông tin của đề thi.
Hàm thông tin của đề được tính bằng tổng các hàm thông tin của câu hỏi thi. Dựa vào thông tin của đề thi ta hoàn toàn tính được sai số tiêu chuẩn của đề thi bới
I ()
công thức: () 1 .
Lord [3] đã đề xuất một quy trình sử dụng các hàm thông tin để thiết kế các ĐTN đáp ứng bất kì yêu cầu mong muốn nào của đặc trưng ĐTN. Quy trình này dựa trên có sẵn một ngân hàng ĐTN và các câu hỏi đã được ước lượng tham số theo IRT.
Các bước quy trình được đề nghị như sau:
(1) Quyết định về hình dáng muốn có của hàm thông tin. Lord gọi đó là hàm thông tin mục tiêu.
(2) Chọn các CH từ ngân hàng đề có hàm thông tin CH sẽ phủ kín các vùng năng lực của hàm thông tin mục tiêu.
(3) Sau mỗi CH được đưa vào ĐTN, tính hàm thông tin của ĐTN bào gồm các CH đã lựa chọn.
(4) Tiếp tục thay thế và lựa chọn các CH để đưa vào ĐTN cho đến khi hàm thông tin của ĐTN tiệm cận với hàm thông tin mục tiêu ở mức độ chấp nhận được.
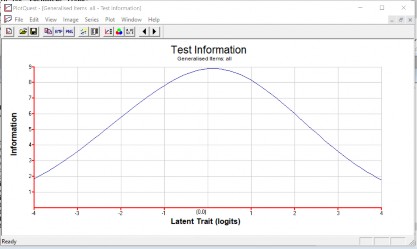
Hình 3.7 Hàm thông tin của đề thi số 1.
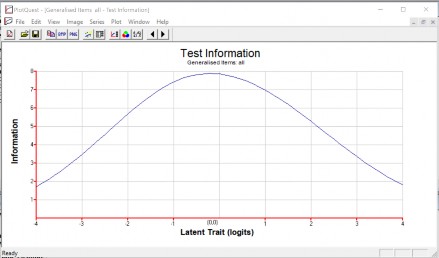
Hình 3.8 Hàm thông tin của đề thi số 2.
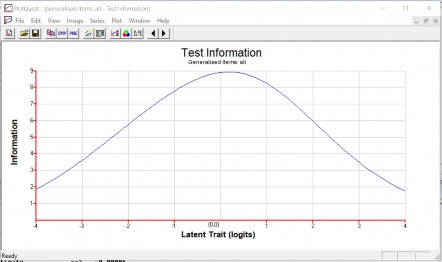
Hình 3.9 Hàm thông tin của đề thi số 3.
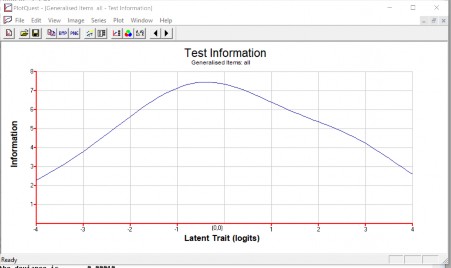
Hình 3.10 Hàm thông tin của đề thi số 4.
Việc so sánh hai hàm thông tin được thực hiện bằng cách tính hiệu suất tỷ
đối của một ĐTN so với một ĐTN khác [3].
RE() I A () . Trong đó
IB ()
RE() là
hiệu suất tỷ đối và
I A () ,
IB ()
là các hàm thông tin tương ứng của ĐTN A và B.