chuyển chúng về một thang đo chung, tức là so bằng. Cũng vậy, nếu hai ĐTN được triển khai trên hai nhóm TS khác nhau để định cỡ (calibration) các CH trắc nghiệm, tức xác định các tham số của chúng, từ mỗi ĐTN sẽ thu được một bộ tham số của các CH. Muốn tham số của các CH của ĐTN thu được từ hai mẫu TS có thể so sánh được với nhau người ta cũng phải dùng thủ thuật so bằng nhằm chuyển các tham số của CH về một thang đo chung. Sau khi so bằng, mỗi giá trị tham số của CH từ hai ĐTN được đặt trên cùng một thang đo nên có thể so sánh với nhau, chẳng hạn để lựa chọn CH có tham số thích hợp nhằm thiết kế một ĐTN theo yêu cầu xác định. Có nhiều thủ tục so bằng khác nhau. Bạn đọc muốn tìm hiểu có thể tham khảo trong [10], hoặc tỉ mỉ hơn trong [13]
1.3.7. Về trắc nghiệm đa phân và trắc nghiệm đa chiều
Khi đặt vấn đề xây dựng mô hình toán phản ánh sự ứng đáp CH ở phần đầu, để đơn giản cho mô hình, chúng ta đã giả thiết là việc ứng đáp kiểu nhị phân (0,1). Tuy nhiên, trong thực tế đánh giá người ta còn sử dụng loại CH với kiểu ứng đáp đa phân (polytomous) hoặc đánh giá một năng lực đa chiều (multidimentionality) hay đánh giá đồng thời nhiều chiều của năng lực. Dưới đây sẽ giới thiệu khái quát về trắc nghiệm đa phân và đa chiều. Đây là các đặc điểm tương đổi mới trong IRT bới sự phức tạp của các mô hình đi kèm, các nghiên cứu chính chủ yếu trong các tài liệu [14], [15]. Các kết quả chủ yếu được công bố từ đầu những năm 2000. Tuy nhiên đây là các ưu điểm nổi trội của IRT, khắc phục việc CTT chỉ phân tích được các câu hỏi nhị phân mà không thể phân tích ĐTN với các câu hỏi nhị phân, đa phân và đa chiều. Theo [3, tr. 218 – 260] ta sẽ xem xét cụ thể các mô hình này.
1.3.7.1. Mô hình trắc nghiệm đa phân
Ngoài các loại trắc nghiệm nhiều lựa chọn mà trả lời theo hai trạng thái nhị phân (0,1), người ta còn sử dụng các loại bảng hỏi (questionaire) với kiểu trả lời theo thang Likert: „‟rất không đồng ý, không đồng ý, đồng ý, rất đồng ý‟‟ trong các điều tra giáo dục hoặc xã hội học nói chung, hoặc các câu hỏi tự luận bao gồm nhiều phần, mỗi phần được định các mức điểm khác nhau, có thể gọi chung là các câu hỏi với ứng đáp đa phân (polytomous). Một số nhà nghiên cứu cũng đã lưu ý đến mô hình trắc nghiệm đa phân từ cuối thập niên 1960 và tập trung mạnh mẽ từ đầu thập niên 1980. Nhà
nghiên cứu quan tâm đến mô hình đa phân sớm nhất có lẽ là Samejima người đã đưa vào mô hình ứng đáp đa cấp (graded response model) [14]. Sau đó có hàng loạt mô hình được đề xuất, nhưng tổng quát nhất có lẽ là mô hình định giá từng phần (Partial Credit Model – PCM) của Master, G.N.
x
Để thiết lập PCM, Masters xét một CH có nhiều hạng (category) điểm để TS đạt được, và giả định rằng xác suất để TS đạt hai hạng điểm kế tiếp nhau tuân theo quy luật của mô hình Rasch nhị phân. Dựa vào giả định nêu trên, khi CH thứ i là đa phân với các hạng điểm 0, 1, 2,..., mi thì Masters thu được xác suất để TS n đạt điểm x của
exp (nik)
CH thứ i sẽ là: Pr ( X ni x) k 0(13) trong đó, để tiện trong việc ký
mi h
exp (nik)
h0 k 0
0
hiệu, chúng ta quy định exp (nik ) 1
k 0
Lưu ý rằng trong biểu thức (13), δik đóng vai trò như b trong mô hình Rasch nhị phân. Với quan niệm của Masters, chúng ta có thể mô tả diễn biến của xác suất trả lời đúng CH (đạt hạng điểm 1) theo năng lực θ của mô hình Rasch nhị phân ứng bởi biểu thức (4) bằng đường cong P(X = 1) và xác suất trả lời sai CH (đạt hạng điểm 0) bằng đường cong P(X = 0) trên cùng một đồ thị ở Hình 1.6
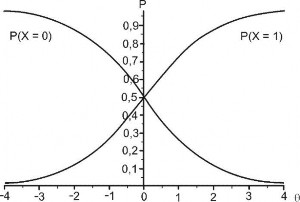
Hình 1.6. Các đường cong ĐTCH trắc nghiệm nhị phân ứng với xác suất trả lời sai P(X = 0) và xác suất trả lời đúng P(X = 1)
Tương tự, trong trường hợp CH có 3 hạng điểm 0, 1 và 2 các đường biểu diễn ứng với 3 hạng điểm có dạng như Hình 1.7
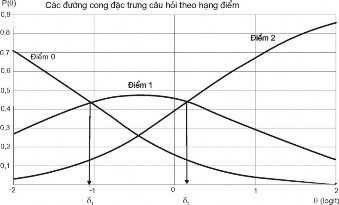
Hình 1.7. Các đường cong ĐTCH của một CH PCM có 3 hạng điểm (với δ1<δ2).
1.3.7.2. Mô hình trắc nghiệm đa chiều
Khi xây dựng các mô hình ứng đáp CH, để đơn giản hoá, chúng ta đã đặt điều kiện về tính đơn chiều (unidimentionality) của CH, tức là CH chỉ đo một thứ năng lực tiềm ẩn, hoặc ta chỉ đo một chiều (dimension) của năng lực tiềm ẩn đa chiều (multidimentionality). Tuy nhiên, trong thực tế, để thực hiện một ứng đáp nào đó, TS thường phải có các chiều khác nhau của năng lực, chẳng hạn để giải một bài toán, TS cần cả kĩ năng đọc hiểu đề toán và các kĩ năng toán học. Reskase đã dựa vào trắc nghiệm nhị phân (0,1) đơn chiều mở rộng ra mô hình trắc nghiệm nhị phân đa chiều [15]. Trong mỗi TS các năng lực tiềm ẩn là khác nhau. Ví dụ khi làm bài kiểm tra toán, thì năng lực giải toán hình học, đại số của TS là khác nhau. Với trường hợp TS có hai chiều năng lực θ1 và θ2, có thể vẽ được mặt cong đặc trưng CH như ở Hình 1.8
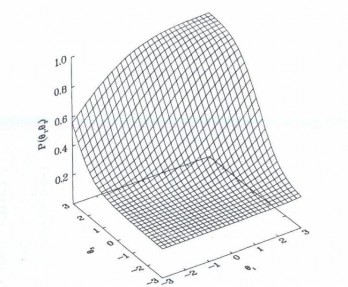
Hình 1.8. Mặt ĐTCH với 2 chiều năng lực θ1,θ2
Về cách biểu hiện tính đa chiều, nhiều nhà nghiên cứu đưa vào khái niệm tính đa chiều giữa các CH và trong từng CH. Một bài trắc nghiệm là đa chiều giữa các CH nếu nó bao gồm nhiều bài trắc nghiệm con đơn chiều. Một bài trắc nghiệm là đa chiều trong từng CH nếu mỗi CH đòi hỏi nhiều chiều năng lực tiềm ẩn để trả lời. Hai kiểu đa chiều của bài trắc nghiệm được minh hoạ ở Hình 1.9.
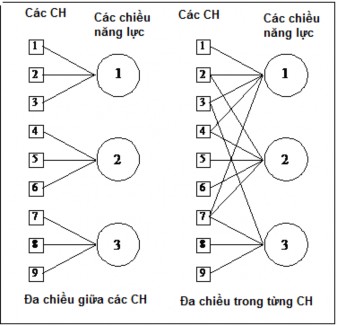
Hình 1.9. Hai kiểu biểu hiện tính đa chiều của các câu hỏi trắc nghiệm.
Ở nửa bên trái Hình 1.9 mô tả bài trắc nghiệm 3 chiều gồm 9 CH theo kiểu đa chiều giữa các CH, mỗi chiều được đánh giá riêng biệt bởi 3 CH. Nửa bên phải của Hình 1.9 mô tả bài trắc nghiệm 3 chiều gồm 9 CH với cả hai kiểu đa chiều giữa các CH và đa chiều trong từng CH, trong đó 4 CH 1, 5, 8, 9 chỉ đo một chiều năng lực, còn các CH khác đo đồng thời 2 hoặc 3 chiều năng lực. [3]
1.3.8. Ví dụ về ước lượng tham số câu hỏi
Với các mô hình IRT 2 và 3 tham số, quá trình ước lượng cũng được thực hiện theo nguyên tắc tương tự như đã mô tả trên đây, tuy số tham số tính toán nhiều hơn. Một trong các thuật toán thường được sử dụng cho quy trình ước lượng nói trên là thuật toán biến cố hợp lý cực đại và nhiều thuật toán khác được trình bày trong [13]. Vì việc thực hiện bài toán ước lượng giá trị năng lực của TS và các tham số của CH khá phức tạp nên đa số bạn đọc thông thường không cần phải bận tâm nhiều đến các thuật toán cụ thể, bởi vì ngày nay đã có nhiều phần mềm chuyên dụng được các
chuyên gia tâm trắc học xây dựng phục vụ các bài toán ước lượng đó. Chẳng hạn sau đây là một số phần mềm được sử dụng tương đối phổ biến hiện nay: CONQUEST của Úc và WINSTEPS của Mỹ cho mô hình Rasch (một tham số) nhị phân và đa phân, BILOG–MG3 của Mỹ cho mô hình 1, 2, 3 tham số nhị phân, PARSCALS, MULTILOG cho mô hình đa phân,... Ở Việt Nam phần mềm đầu tiên phục vụ cho bài toán này là VITESTA, cho các mô hình 1, 2, 3 tham số nhị phân và đa phân, được công ty EDTECH–VN xây dựng từ năm 2007 [2]. Ta xét một ví dụ cho quá trình ước lượng các tham số của câu hỏi.
Để phù hợp với quá trình tính toán bằng tay ta xét một hình một tham số. Chúng ta xem xét một bài kiểm tra điển hình. Với N câu hỏi và với M người tham gia kiểm tra. Điểm số của những người kiểm tra này sẽ được phân bổ trong một mức độ khả năng về dải năng lực của thí sinh. Những người kiểm tra này được chia thành J số nhóm cùng có cùng năng lực để tất cả người kiểm tra trong một nhóm nhất định có cùng cấp độ năng lực θj và sẽ có mj người kiểm tra bên trong nhóm j, trong đó j = 1, 2,
3. . . J. Xét một câu hỏi nào đó thì trong cùng một nhóm có rj người kiểm tra trả lời đúng câu hỏi đã cho. Như vậy, ở mức độ năng lực θj,tỷ lệ đáp ứng đúng là p(θj) = rj / mj, là ước tính của xác suất trả lời chính xác ở mức khả năng θj. Bây giờ có thể thu được giá trị của rj và p (θj) được tính cho mỗi cấp độ khả năng j được thiết lập theo dải năng lực J. Nếu tỷ lệ đáp ứng chính xác trong mỗi nhóm khả năng được vẽ, kết quả sẽ là giống như thể hiện trong hình 1.10
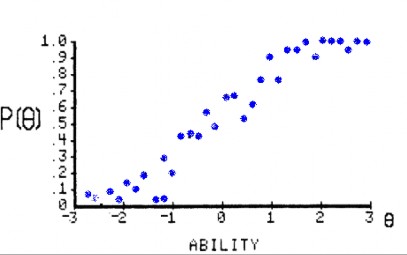
Hình 1.10. Mô tả đáp ứng câu hỏi
Nhiệm vụ tiếp theo là tìm ra đường cong đặc trưng của câu hỏi (ICC) phù hợp nhất với tỷ lệ phản ứng đúng hay kết quả làm bài đối với câu hỏi của thí sinh. Để làm như vậy, một mô hình cần phải được lựa chọn cho các ICC. Mặc dù bất kỳ một trong ba mô hình có thể được sử dụng, mô hình hai tham số được sử dụng ở đây với
eab
P()
1 eab
. Các thủ tục được sử dụng để phù hợp đường cong dựa trên ước
tính khả năng ước lượng tối đa. Theo cách tiếp cận này, giá trị ban đầu cho các thông số của câu hỏi cần được khởi tạo trước, chẳng hạn như b = 0.0, a = 1.0. Sau đó, sử dụng các ước lượng để tính giá trị của P(θj) được tính tại mỗi nhóm năng lực thông qua phương trình cho ICC mô hình. Lưu ý giá trị quan sát được của năng lực p(θj) và giá trị tính toán P (θj) được xác định trên tất cả các nhóm năng lưc. Sau đó, điều chỉnh các tham số câu hỏi (a, b) ước tính được để kết quả giữa P (θj) và p(θj) gần sát nhau hơn nữa. Khi đó ICC được xác định bởi các giá trị ước tính toán của các tham số thông kê và tỷ lệ quan sát được của đường cong đặc trưng câu hỏi. Quá trình điều chỉnh ước tính này là tiếp tục cho đến khi các điều chỉnh quá nhỏ mà ít sự sai số giữa P (θj) và p(θj) không còn đáng kể. Tại thời điểm này, thủ tục ước lượng được chấm dứt và các giá trị hiện tại của b và a là ước lượng tham số câu hỏi. Với các giá trị này, phương trình cho ICC được sử dụng để tính xác suất phản ứng chính xác P (θj) ở mỗi cấp độ năng lực và ICC có thể được vẽ. Đường cong kết quả là ICC phù hợp nhất với dữ liệu phản hồi của mục đó. Hình 2.2 cho thấy một ICC phù hợp với tỷ lệ quan sát được của phản ứng chính xác thể hiện trong hình 2.1. Các giá trị ước tính của các thông số mục là b = -37 và a = 1,25.
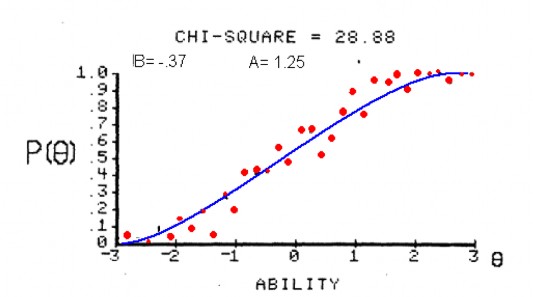
Hình 1.11 Hàm đặc trưng câu hỏi
eaibi
a b i i
Như vậy với câu hỏi i nào đó sẽ có hàm đặc trưng câu hỏi Pi () .
1 e
Để xét sự trùng khớp giữa P (θj) và p(θj) tốt người ta thường dùng chỉ số Chi- bình
J [p() P()]2
phương
2 mj j
nhỏ hơn một số tiêu chuẩn chọn trước nào. Với các
j 0
j P(
j )(1P(j ))
câu hỏi mà quá trình trên khó hội tụ giữa hai giá trị P (θj) và p(θj) (Chi- bình phương luôn lớn số tiêu chuẩn được chọn) thì câu hỏi đó nên bị loại vì yếu tố kĩ thuật. Đó là mô hình đường cong được chọn không phù hợp (một, hai, ba tham số, …) hoặc giá trị đáp ứng câu hỏi này rất phân tán nên phải chỉnh sửa lại câu hỏi hoặc loại bỏ.
Để đơn giản ta xét ví dụ sau, chúng ta hãy nhìn vào một ví dụ minh hoạ số cho ước lượng tham số câu hỏi. Để đơn giản và dễ hiểu ta xét mô hình Single Parameter của Rasch minh hoạ. Do đó, một tham số duy nhất là độ khó của câu hỏi được ước tính. Chúng ta hãy lấy một ví dụ về một bài kiểm tra loại khách quan gồm 20 bài cho 76 thí sinh. Bảng dưới đây minh họa dữ liệu về số điểm bên phải và số người kiểm tra nhận được mỗi điểm:
Bảng 1.4. Dữ liệu thử nghiệm của câu hỏi thi
Số người trong nhóm | Số câu trả lời đúng của nhóm năng lực trên tổng số người của nhóm | Xác xuất trả lời đúng p(θj) = rj / mj | |
18 | 4 | 4 | 1 |
17 | 4 | 4 | 1 |
16 | 5 | 2 | 0.4 |
15 | 12 | 5 | 0.41 |
14 | 7 | 1 | 0.14 |
13 | 10 | 6 | 0.6 |
12 | 8 | 2 | 0.25 |
11 | 11 | 1 | 0.09 |
10 | 5 | 1 | 0.2 |
9 | 6 | 0 | 0 |
8 | 2 | 1 | 0.5 |
7 | 1 | 1 | 1 |
6 | 1 | 0 | 0 |
Có thể bạn quan tâm!
-
 Các Tham Số Đặc Trưng Của Cầu Hỏi Trắc Nghiệm Và Phân Tích Đề Trắc Nghiệm
Các Tham Số Đặc Trưng Của Cầu Hỏi Trắc Nghiệm Và Phân Tích Đề Trắc Nghiệm -
 Thứ Hạng Bách Phân (Percentile Ranks, Thường Viết Là Pr)
Thứ Hạng Bách Phân (Percentile Ranks, Thường Viết Là Pr) -
 Các Đường Cong Đtch Hai Tham Số Với Các Giá Trị A Khác Nhau (B= 0)
Các Đường Cong Đtch Hai Tham Số Với Các Giá Trị A Khác Nhau (B= 0) -
 Dữ Liệu Tính Toán Ước Lượng Hàm Đặc Trưng Câu Hỏi
Dữ Liệu Tính Toán Ước Lượng Hàm Đặc Trưng Câu Hỏi -
 Qui Trình Xây Dựng Ngân Hàng Câu Hỏi Trắc Nghiệm Khách Quan
Qui Trình Xây Dựng Ngân Hàng Câu Hỏi Trắc Nghiệm Khách Quan -
 Triển khai đánh giá kết quả học tập môn Toán lớp 12 bằng một đề tổng hợp với các câu hỏi nhị phân, đa phân và đa chiều - 10
Triển khai đánh giá kết quả học tập môn Toán lớp 12 bằng một đề tổng hợp với các câu hỏi nhị phân, đa phân và đa chiều - 10
Xem toàn bộ 137 trang tài liệu này.
Đối với tỷ lệ câu trả lời đúng và nhóm điểm số bên phải cho ở trên, đồ thị được vẽ với một ICC gần đúng như hình dưới đây
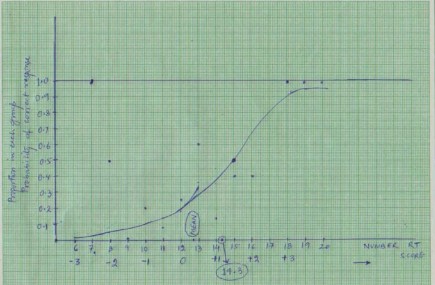
Hình 1.12. Ước lượng hàm đặc trưng của câu hỏi