Dữ Liệu Tính Toán Ước Lượng Hàm Đặc Trưng Câu Hỏi

Một biểu đồ đồ họa thô của tỷ lệ các câu trả lời đúng ở mọi năng lực, số điểm được vẽ lên đối với số điểm đúng được thu được bằng phương pháp thử và sai số trong đường cong phù hợp. Biểu diễn thô được đưa ra trong đồ thị. Có thể thấy rằng điểm của đường cong của đáp ứng được nhìn thấy ở một số điểm số bên phải là 15 tương ứng với một thô ước tính 15 số đúng số và tương ứng +1.5 trên thang điểm về khả năng như đã nêu trong đồ thị. Giả sử ước tính đầu tiên của độ khó b, của câu hỏi này

1.5. Cho một một tham số b = 1.5, ICC hoặc IRF thu được bằng cách sử dụng phần mềm BIRT như hình dưới đây:

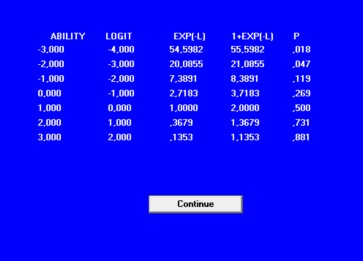
Hình 1.13 Tham số ước lượng của câu hỏi

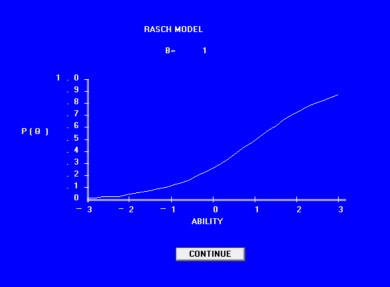
Hình 1.14 Đồ thị hàm đặc trưng của câu hỏi

Đường cong BIRT của Pi (θ) ở tất cả các giá trị từ -3 đến +3 có thể được so sánh với đạt được tỷ lệ các câu trả lời đúng ở mức điểm số ngay ở mức tương ứng giả định mức độ khả năng như thể hiện trong bảng dưới đây:

Bảng 1.5 Dữ liệu tính toán ước lượng hàm đặc trưng câu hỏi

Nhóm năng lực

Xác xuất trả lời đúng quan sát được pi (θj)	Dải năng lực	Xác xuất đáp ứng câu hỏi của nhóm năng lực Pi (θj)
18	1.0	+3	0.894
17	1.0	+2.5	0.805
16	0.4	+2	0.67
15	0.41	+1.5	0.5
14	0.14	+1	0.33
13	0.6	+0.5	0.195
12	0.25	+0	0.106
11	0.09	-0.5	0.055
10	0.2	-1	0.028
9	0	-1.5	0.014
8	0.5	-2	0.007
7	1	-2.5	0.003
6	0	-3	0

Có thể bạn quan tâm!

Xem toàn bộ 137 trang tài liệu này.

Ta có hàm một tham số

b

P() 

1 eb

với b =1.5 thì

1.5

P() 

1 e1.5

J [p() P()]2

Chi bình phương được tính từ công thức

2 mj j

j 0

j P(

j )(1P(j ))

Bảng 1.6. Dữ liệu tính toán ước lượng hàm đặc trưng câu hỏi

Nhóm năng lực

Số người trong nhóm mj	Xác xuất trả lời đúng quan sát được pi (θj)	Xác xuất đáp ứng câu hỏi của nhóm năng lực Pi (θj)	Q(θj)=1- P(θj)	[p() P()]2 j j	2
18	4	1.0	0,894	0,106	0,011236	0,474273
17	4	1.0	0,805	0,195	0,038025	0,968944
16	5	0.4	0,67	0,33	0,0729	1,648575
15	12	0.41	0,5	0,5	0,0081	0,3888
14	7	0.14	0,33	0,67	0,0361	1,142922
13	10	0.6	0,195	0,805	0,164025	10,44912
12	8	0.25	0,106	0,894	0,020736	1,750538
11	11	0.09	0,055	0,945	0,001225	0,259259
10	5	0.2	0,028	0,972	0,029584	5,435038
9	6	0	0,014	0,986	0,000196	0,085193
8	2	0.5	0,007	0,993	0,243049	69,9321
7	1	1	0,003	0,997	0,994009	332,3333
6	1	0	0	1	0	0
						424,8681

Như vậy chỉ số 2 là quá lớn ta phải thay đổi tham số b (theo hai chiều hướng:

tăng lên và giảm đi) ví dụ b=1.51.451.4…1, giảm (tăng) đến khi chỉ số 2

nhỏ trong ngưỡng cho phép. Quá trình kết thúc khi các ứng đáp câu hỏi quan sát được và ước lượng tham của câu hỏi có đồ thị “tiệm cận” với nhau như hình vẽ.

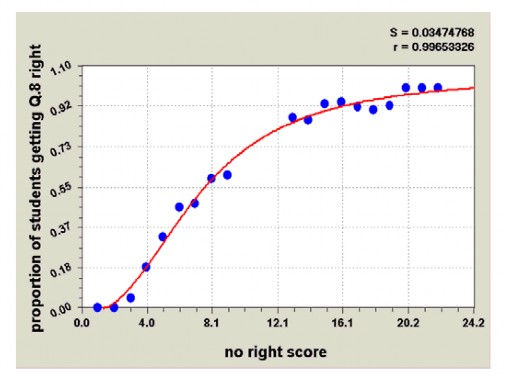
Hình 1.15. Đồ thị của hàm đặc trưng câu hỏi

Nếu quá trình trên không thu được 2

ta sửa lại câu hỏi.

hợp lý thì hoặc là ta bỏ câu hỏi thi, hai là

Lưu ý quá trình ước lượng trên không phụ thuộc vào mẫu (nếu mẫu có năng lực thấp, hay năng lực cao đều không ảnh hưởng tới quá trình ước lượng tham số). Đây là một ưu điểm nổi bất của IRT. Nó giúp ta có thể ước lượng đề thi với các mẫu không phổ quát mà vẫn không lo ảnh hưởng tới chất lượng đề thi.

Dưới đây là hình ảnh ước lượng tham số câu hỏi với tập mẫu khác nhau

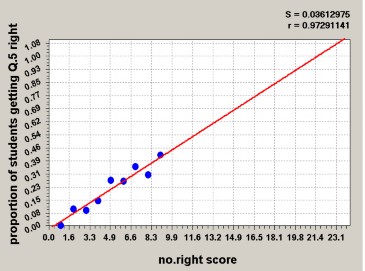
Hình 1.16.. Hình ảnh ước lượng tham số câu hỏi với tập mẫu có năng lực thấp

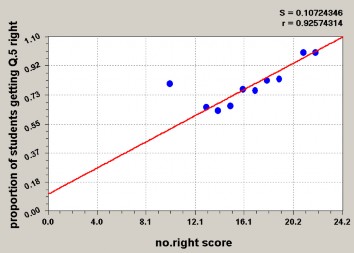
Hình 1.17. Hình ảnh ước lượng tham số câu hỏi với tập mẫu có năng lực cao

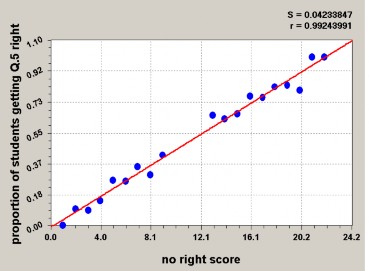
Hình 1.18. Hình ảnh ước lượng tham số câu hỏi với tập mẫu có năng lực phổ quát

Khi tất cả các câu hỏi trong đề thi được ước lượng tham số, tức là với mỗi câu

eaibi

hỏi i nào đó ta có hàm đặc trưng của nó:

Pi () . Trong một đề có N câu

a b i i

1 e

hỏi thi, ta sẽ có tương ứng n hàm đặc trưng cho từng câu hỏi thi.

Mặc dù giả định rằng thang đo số liệu được biết đến, các giá trị số của các tham số câu hỏi thi và các thông số về khả năng của người kiểm tra có thể được thể hiện bằng số liệu này. Các nhà soạn đề thi cần biết những đặc tính nào họ cần đo lường về thí sinh để thiết kế các hỏi thi phù hợp cho những thí sinh có khả năng thấp, trung bình hoặc cao. Nhưng không thể xác định các giá trị của các tham số của độ phân biệt a giữa các nhóm thí sinh cần đo. Ngoài ra, khi một bài kiểm tra được thực hiện cho một nhóm thí sinh, không biết trước bao nhiêu của các đặc điểm tiềm ẩn của mỗi người thí sinh sở hữu. Do đó, một nhiệm vụ chính là xác định các giá trị của tham số câu hỏi và khả năng của thí sinh trong một câu hỏi cho các đặc điểm ẩn tiềm ẩn. Trong IRT, nhiệm vụ này là được gọi là hiệu chuẩn kiểm tra, và nó cung cấp một khung tham khảo để giải thích các kết quả kiểm tra. Kiểm tra hiệu chuẩn được thực hiện bằng cách thực hiện một bài kiểm tra cho một nhóm thí sinh M và câu trả lời nhị phân của thí sinh đối với N câu hỏi trong đề thi. Sau đó các công thức, thủ tục toán học được áp dụng cho dữ liệu ứng đáp câu hỏi để tạo ra mô hình năng lực, mô phỏng bám sát năng lực tiềm ẩn của thí sinh. Sau đó, các giá trị của ước lượng tham số câu hỏi và năng lực của thí sinh được thể hiện bằng số liệu này.

2.1. Đặt vấn đề

CHƯƠNG 2

TỔ CHỨC VÀ THỰC HIỆN XÂY DỰNG ĐỀ THI

Cho đến nay các loại lý thuyết đo lường và các mô hình đo lường khác nhau đã được giới thiệu rộng rãi ở Việt Nam trong. Với mong muốn tiếp cận lý thuyết khảo thí hiện đại, luận văn này dự định tập trung vào nghiên cứu trong lĩnh vực kiểm tra môn toán học lớp 12 bằng lý thuyết IRT. Lý thuyết IRT đã được biết đến từ những năm 50 của thế kỷ trước và được giới thiệu về Việt Nam từ những năm 2000, nhưng hiện nay việc xây dựng một đề thi trên cơ sở lý thuyết IRT vẫn chưa được phổ biến. Cách xây dựng đề thi vẫn chủ yếu theo lý thuyết đánh giá cổ điển (các kì thi THPT QG là ví dụ), IRT mới chủ yếu được ứng dụng trong các phân tích kết quả thi. Có nhiều lý do cho vấn đề này. Thực ra các lý thuyết kiểm tra cổ điển và lý thuyết IRT không loại trừ, đối lập nhau mà thường bổ xung các ưu điểm cho nhau. Mặt khác việc thực thi, ứng dụng lý thuyết IRT vào việc xây dựng đề thi ở Việt Nam gặp nhiều khó khăn. Thứ nhất là đội ngũ nghiên cứu chuyên sâu ở trong nước là chưa nhiều, chưa có cộng đồng. Thứ hai các mô hình toán học phức tạp trong IRT cần có những công cụ, phần mềm chuyên dụng để tính toán. Thứ ba lý thuyết đánh giá cổ điển vẫn đáp ứng tương đối tốt các yêu cầu từ các kỳ thi của bộ giáo dục.

Tuy vậy, thực tế đo lường trong giáo dục là vấn đề ngày càng được quan tâm sát sao trước yêu cầu đổi mới kiểm tra đánh giá trong giáo dục. Các nền tảng của đo lường đánh giá được biết đến hiện nay hoặc là dựa trên lý thuyết kiểm tra cổ điển hoặc dựa trên IRT hoặc là sự kết hợp của cả hai. Dựa trên các hiểu biết hạn hẹp của cá nhân, luận văn cố gắng xây dựng một đề đánh giá môn toán lớp 12 trên cở sở của lý thuyết khảo thí hiện đại.

2.2. Quy trình xây dựng một đề thi, đề kiểm tra

Một đề kiểm tra tiêu chuẩn hóa thường được thiết kế bởi các câu hỏi (CH) chọn từ một ngân hàng câu hỏi (NHCH). NHCH là tập hợp một số lượng tương đối lớn các câu hỏi, trong đó mỗi CH được mô tả gắn với các phần nội dung xác định và các tham số của nó. Trong trường hợp CH trắc nghiệm thì đó là độ khó, độ phân biệt theo lý

thuyết trắc nghiệm cổ điển, là các tham số a, b, c theo IRT. Ngoài ra NHCH phải được thiết kế sao cho trên đó có thể thực hiện các thao tác loại trừ hoặc thay đổi các CH “xấu”, bổ xung các CH tốt để số lượng và chất lượng câu hỏi ngày càng tăng lên. [A4]. Thiết kế một đề kiểm tra tiêu chuẩn hóa và một NHCH là khá phức tạp và tốn nhiều công sức, trí lực và thời gian. Trong luận văn này, sẽ xem xét việc thiết kế đề kiểm tra tổng kết môn Toán lớp 12. Có thể tóm tắt các bước đó như sau:

1) Tên đề thi

2) Mục đích đề thi, đề kiểm tra.

3) Khối lượng kiến thức, kĩ năng cần đo lường

4) Đối tượng đo lường

5) Những loại hình kiểm tra/ thi thực hiện

6) Mục đích sử dụng kết quả thi

7) Thời gian thi

8) Bảng ma trận trọng số

9) Biên soạn đề

10) Đề thi và đáp án.

Để thực hiện các bước của quy trình trên, chúng ta cần xác định các nội dung chi tiết của môn học, các mức độ nhận thức mong muốn TS đạt được rồi từ đó xây dựng ma trân kiến thức của môn học. Dựa vào các đặc điểm của kì thi, phân bố thời lượng nội dung kiểm tra mà ta phân bố tỉ lệ các CH hợp lí. Việc phân công, chế tác các CH thi cũng rất quan trọng. Mọi người được phân công biên soạn CH phải có năng lực chuyên môn vững vàng, nắm chắc các ô ma trận kiến thức để biên soạn các CH một cách chính xác và tốt nhất. Ngoài ra việc phản biện chuyên gia, lập các đề thi thử với các CH đã được soạn cũng phải làm hết sức nghiêm túc, khoa học. Những người quan tâm đến việc xây dựng một bài kiểm tra phải đối mặt với những khó khăn thử thách liên quan như: Đánh giá cái gì, đánh giá như thế nào, và liệu các test có tin cậy hay không, có cơ sở vững chắc không. Đó là những thử thách cơ bản đối với người giáo viên xây dựng test cho chính mình.