Trắc nghiệm tiêu chuẩn hoá thường do các chuyên gia phụ trách chuyên môn đặc thù soạn thảo, và phải kiểm thử nhiều lần, do đó mỗi câu hỏi trắc nghiệm được gắn với các chỉ số cho biết thuộc tính và chất lượng của nó như độ khó, độ phân biệt.
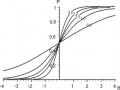
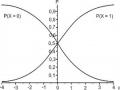
Trong các kiểu câu trắc nghiệm, kiểu câu nhiều lựa chọn có cách trả lời đơn giản nhất. Câu đúng - sai là một trường hợp riêng của câu nhiều lựa chọn với hai phương án trả lời. Dễ dàng thấy rằng khi một người hoàn toàn không có hiểu biết đánh dấu hú hoạ để trả lời một câu hỏi đúng - sai thì xác suất để anh ta làm đúng là 1/2 hoặc 50%, cũng vậy nếu anh ta đánh dấu hú hoạ để trả lời câu trắc nghiệm với n phương án trả lời thì xác suất để anh ta làm đúng là 1/n. Trong các kiểu câu trắc nghiệm, kiểu câu nhiều lựa chọn thường được sử dụng vì chúng có cấu trúc đơn giản, dễ xây dựng thành các bài thi, dễ chấm điểm. Về vị trí quan trọng của kiểu câu hỏi NLC nêu dưới đây chúng ta sẽ nói kỹ hơn về chúng. Loại câu trắc nghiệm nhiều lựa thường được dùng trong các kì thi là loại có bốn phương án trả lời, vì số phương án như vậy vừa đủ để giảm xác suất làm đúng do đoán mò hú hoạ xuống còn 25%, đồng thời câu cũng không quá phức tạp khó xây dựng. Câu trắc nghiệm nhiều lựa chọn cung cấp thông tin cần thiết hoặc nêu một câu hỏi và các phương án để chọn, và được đánh dấu bằng các chữ cái A, B, C, D... hoặc các chữ số 1, 2, 3... trong các phương án để chọn và chỉ có duy nhất một phương án đúng, các phương án khác được đưa vào có tác dụng “gây nhiễu” (distractor) đối với thí sinh. Nếu câu NLC được soạn tốt thì một người không nắm vững vấn đề sẽ không thể nhận biết được trong tất cả các phương án để chọn đâu là phương án đúng, đâu là phương án nhiễu. Một số chuyên gia trắc nghiệm ở phía Nam còn gọi các phương án nhiễu là “mồi nhử”.
Trong khi soạn thảo câu trắc nghiệm, người ta thường cố gắng làm cho các phương án nhiễu đều có vẻ “có lý” và “hấp dẫn” như phương án đúng. Đôi với tất cả các môn học người ta đều có thể viết câu hỏi trắc nghiệm. Tuy nhiên, do đặc thù của từng môn học mà việc viết trắc nghiệm cho môn này có thể khó hơn cho môn kia. Cần lưu ý rằng không phải bất cứ ai có kiến thức chuyên môn cũng viết được câu trắc nghiệm có chất lượng cao cho chuyên môn đó. Muốn viết câu hỏi trắc nghiệm tốt phải suy nghĩ sâu sắc về chuyên môn và tích lũy kinh nghiệm sau một thời gian thử nghiệm lâu dài.
2.2.1. Qui trình xây dựng ngân hàng câu hỏi trắc nghiệm khách quan
Như đã nói ở phần trên, để hoàn thiện các bài trắc nghiệm người ta phải triển khai các trắc nghiệm thử. Thử nghiệm các câu hỏi trắc nghiệm nhằm tìm ra các các hỏi xấu và định cỡ về độ khó cho đề trắc nghiệm. Phép đo này có thể thực hiện được nhờ hiệu phép thống kê. Để đo được năng lực thí sinh, thước đo - bài trắc nghiệm phải được định cỡ (calibrration) tỉ mỉ, tức là phải biết được các độ khó, độ phân biệt của các câu, độ tin cậy và độ giá trị của bài trắc nghiệm. Tuy chưa được định cỡ như vậy, qua nhiều bước soạn thảo ngân hàng câu hỏi theo quy trình như nêu ở phần đầu, bài trắc nghiệm cũng đã tương đối đảm bảo chất lượng để có thể phân loại được thí sinh. Những thí sinh nào làm đúng nhiều câu hỏi, họ thuộc nhóm nhóm giỏi, những thí sinh làm đúng ít câu hỏi, họ thuộc nhóm kém. Như vậy, dựa vào điểm số của toàn bài trắc nghiệm như một thước đo để định cỡ các câu và bài trắc nghiệm.
Cần lưu ý một điều là khi dùng từ “trắc nghiệm thử” thì chữ “thử” chỉ có ý nghĩa về chuyên môn trong thiết kế và định cỡ trắc nghiệm, còn trong cuộc sống phải tạo tình huống để mọi thí sinh để coi lần trắc nghiệm đó là thật, vì có như vậy thì họ mới làm nghiêm túc, hết mình và phép thử mới đạt yêu cầu.
Dựa vào kết quả trắc nghiệm thử người ta có thể tính bằng tay để phân tính bài các câu và bài trắc nghiệm, cũng có thể nhờ các phần mềm giúp tính rất nhanh chóng các đại lượng cần thiết nhờ các phép tính thống kê tương quan cổ điển, hoặc các phần mềm được xây dựng theo các mô hình toán học về đo lường giáo dục. [6]
2.2.2. Quy trình triển khai một kỳ thi trắc nghiệm khách quan
Quy trình tổ chức xây dựng đề và tổ chức kỳ thi trắc nghiệm tiêu chuẩn hoá rất phức tạp. Có thể tóm tắt các bước của quy trình đó như sau:
(1) Xác định các môn thi và những nội dung tổng quát cần kiểm tra đối với từng môn. Đồng thời, định ra yêu cầu về các mức kỹ năng, chẳng hạn: nhớ, hiểu, biết vận dụng, phân tích, tổng hợp... Để thực hiện bước này người ta thường lập một ma trận 2 chiều: các dòng phân theo các phần nội dung, các cột phân theo các mức kỹ năng, trong mỗi ô ghi số câu hỏi cần thiết (hoặc tỷ lệ phần trăm) của phần nội dung và mức kỹ năng tương ứng.
(2) Phân công cho các giáo viên, viết một số câu trắc nghiệm theo các yêu cầu cụ thể về nội dung và mức kỹ năng đã xác định theo các bảng, mẫu quy ước.
(3) Trao đổi trong từng nhóm biên soạn giúp các tác giả phát hiện và sửa chữa được nhiều sai sót mà bản thân không cảm thấy.
(4) Biên tập và đưa các câu trắc nghiệm vào "ngân hàng" lưu trong máy tính theo quy tắc và quy ước sẵn. Ngân hàng câu hỏi thường được quản lý bằng một phần mềm chuyên dụng.
(5) Lập đề thi mẫu và tổ chức thử nghiệm trên một mẫu đại diện.
(6) Chấm thi và thống kê, phân tích các kết quả thi thử nhằm xác định độ khó, độ phân biệt, qua đó có thể đánh giá độ tin cậy của câu hỏi, đề thi trắc nghiệm.
(7) Thay thế, chỉnh sửa các câu hỏi kém chất lượng và nhập các câu hỏi chất lượng vào ngân hàng đề thi.
(8) Ra đề thi chính thức: căn cứ vào cấu trúc đề thi (phân bố câu theo nội dung và mức độ kỹ năng tương ứng bảng ma trân đặc trưng), nhờ phần mềm tin học để chọn một cách ngẫu nhiên từ ngân hàng số câu hỏi cần thiết với các đặc trưng xác định (độ khó, độ phân biệt, mức kỹ năng) để lập nên một đề thi. Các công cụ phần mềm sẽ giúp ta xây dựng các đề tương đương một cách đơn, nhẹ nhàng (đảo câu, đảo đáp án,…)
(9) In đề thi và tổ chức thi: đề thi được in sẵn, phát cho từng thí sinh trong phòng thi.
(10) Chấm và phân tích thống kê các kết quả thi: ngày nay người ta có thể chấm lại trắc nghiệm trên các hệ thống tự động gồm một máy quét quang học và máy tính có phần mềm tin học hỗ trợ việc chấm thi.
(11) Công bố kết quả thi.
Để xây dựng được ngân hàng câu hỏi thi phong phú, ta cần lặp đi, lặp lại các bước ở trên để từ đó liên tục bổ xung các hỏi tốt và loại trừ các câu hỏi xấu, câu hỏi đã dùng hoặc lỗi thời . Qua đó có thể thấy rằng ngân hàng các câu trắc nghiệm không phải là kho lưu trữ bất động mà như một cơ thể sống, luôn được bổ sung, loại bỏ, hoàn thiện và phát triển. [3]
Cần phải nhấn mạnh rằng các câu trắc nghiệm tiêu chuẩn hoá trong ngân hàng và đề thi trắc nghiệm phải được bảo mật trước khi đem ra sử dụng. Những đề thi và
những câu hỏi đã được dùng chính thức thường được công bố ở các tài liệu dùng cho tham khảo hoặc luyện thi.
Một tác dụng hết sức quan trong của các kỳ thi đại trà bằng trắc nghiệm tiêu chuẩn hoá là những thông tin thu được qua việc phân tích thống kế toàn bộ bài làm của thí sinh qua các kỳ thi là những số liệu hết sức quý báu để đánh giá định lượng về tình hình giáo dục của từng khu vực, từng cộng đồng, từng nhóm thí sinh và đánh giá xu thế phát triển của chất lượng giáo dục theo thời gian.
2.3. Xây dựng đề thi môn toán
Người ta có thể áp dụng phương pháp trắc nghiệm để tổ chức thi, kiểm tra ở các lớp học thông thường với số thi sinh không quá lớn, cũng có thể áp dụng ở các kỳ thi quy mô lớn hàng nghìn, hàng vạn thí sinh. Trong trường hợp sau, bất kỳ một sơ suất nhỏ nào cũng có thể dẫn đến những hậu quả xấu và những phản ứng xã hội bất lợi. Do đó, để triển khai một kỳ thi quy mô lớn người ta phải chuẩn bị hết sức cẩn thận về đề thi quy trình thi, thể thức chấm điểm, cách công bố kết quả... Quá trình chuẩn bị đó hết sức công phu và tốn kém mà một kỳ thi thông thường ở lớp học không thể làm nổi. Ta có chu trình xây dựng như sau:
Bảng 2.1 Quy trình xây dựng đề thi
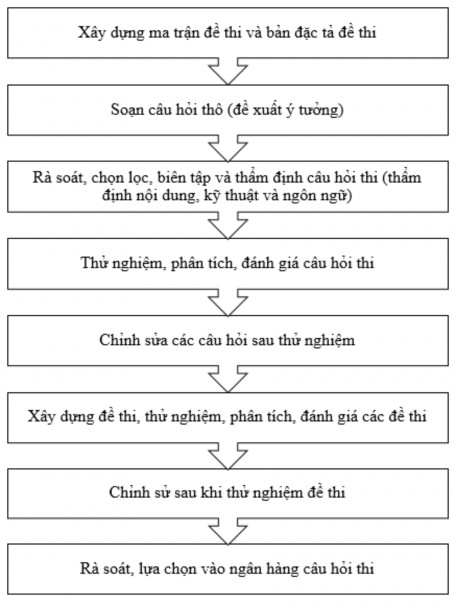
Kỳ thi được chuẩn bị công phu như vậy được coi là kỳ thi tiêu chuẩn hoá. Các câu hỏi trong một đề thi tiêu chuẩn hoá là các câu hỏi đã được thử nghiệm, định cỡ trên cơ sở phân tích các tham số độ khó, độ phân biệt, độ tin cậy, độ giá trị của từng câu.
2.3.1. Chuẩn bị
Để xây dựng đề thi một cách chuẩn mực và khoa học ta cần làm rõ các bước các vấn đề sau:
(1) Tên đề thi : “ Kiểm tra môn toán học lớp 12”
(2) Mục đích đề thi, đề kiểm tra: “ Đánh giá, kiểm tra kiến thức môn toán lớp 12 của học sinh THPT”
(3) Khối lượng kiến thức, kĩ năng cần đo lường: “ Toàn bộ chương trình toán 12 theo chuẩn kiến thức, kĩ năng của BGD”
(4) Đối tượng đo lường: “ Học sinh học hết chương trình toán 12”
(5) Những loại hình kiểm tra/ thi thực hiện: “Dựa vào các phân tích ở các phần trên ta chọn hình thức thi trắc nghiệm đa lựa chọn – bốn lựa chọn”
(6) Mục đích sử dụng kết quả thi: Kết quả thi được sử dụng để xét tốt nghiệp THPT của thí sinh và tuyển sinh đầu vào cho các trường đại học tại Việt Nam.
(7) Thời gian thi: 90 phút
2.3.2. Xây dựng bảng ma trận trọng số
Để xây dựng bảng ma trận trọng số của đề thi ta dựa vào các tài liệu sau:
(1) Hướng dẫn chuẩn kiến thức kĩ năng toán 12 do bộ giáo dục phát hành năm 2006 [9]
(2) Phân phối chương trình chuẩn toán 12 – phụ lục 1.
(3) Dựa vào phân bố thời gian, nội dung kiến thức và mục địch sử dụng kết quả thi ta xây dựng ma trận trọng số các câu hỏi thi như sau:
Bảng 2.2. Ma trận đề thi môn toán 12
MA TRẬN ĐỀ THI MÔN TOÁN LỚP 12
Các chủ đề | Mức độ kiến thức đánh giá | Tổng số câu hỏi | |||||
Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | ||||
1 | Hàm số và các bài toán liên quan | 4 | 4 | 2 | 1 | 11 | |
2 | Mũ và Lôgarit | 4 | 4 | 1 | 1 | 10 | |
3 | Nguyên hàm – Tích phân và ứng dụng | 2 | 3 | 1 | 1 | 7 | |
4 | Số phức | 3 | 2 | 1 | 0 | 6 | |
5 | Thể tích khối đa diện | 1 | 2 | 1 | 1 | 5 | |
6 | Khối tròn xoay | 1 | 1 | 1 | 0 | 3 | |
7 | Phương pháp tọa độ trong không gian | 4 | 2 | 1 | 1 | 8 | |
Tổng | Số câu | 19 | 18 | 8 | 5 | 50 | |
Tỷ lệ | 38 % | 36 % | 16 % | 10 % | |||
Có thể bạn quan tâm!
-
Các Đường Cong Đtch Hai Tham Số Với Các Giá Trị A Khác Nhau (B= 0) -
Về Trắc Nghiệm Đa Phân Và Trắc Nghiệm Đa Chiều -
Dữ Liệu Tính Toán Ước Lượng Hàm Đặc Trưng Câu Hỏi -
Triển khai đánh giá kết quả học tập môn Toán lớp 12 bằng một đề tổng hợp với các câu hỏi nhị phân, đa phân và đa chiều - 10 -
Phân Tích Câu Hỏi Thi Bằng Lý Thuyết Khảo Thí Hiện Đại -
Bản Đồ Phân Bố Độ Khó Câu Hỏi Thi Và Năng Lực Thí Sinh
Xem toàn bộ 137 trang tài liệu này.
Để chuẩn bị cho việc biên soạn câu hỏi ta chuẩn bị bảng đặc tả về nội dung môn toán lớp 12. Phụ lục 2. Từ đó ta có bảng mô tả mức độ các câu hỏi (mặc định mỗi câu hỏi 1 điểm ) như sau:
Bảng 2.3 Bảng mô tả chi tiết từng câu hỏi trong đề thi
BẢNG MÔ TẢ CHI TIẾT NỘI DUNG TỪNG CÂU HỎI
CÂU | MÔ TẢ | |
1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số (11 câu) | Nhận biết: Nhận biết đồ thị của hàm số bậc ba, bậc 4 trùng phương, hàm số y ax b , tương giao giữa các đồ thị đơn mx n giản. | |
Nhận biết: Xác định khoảng đồng biến , nghich biến của hàm số bậc ba, hàm bậc bốn trùng phương thông qua bảng biến thiên của hàm số. | ||
Nhận biết: Nhận biết cực trị của hàm số bậc ba, bậc bốn thông qua bảng biến thiên | ||
Nhận biết: Nhận biết phương trình tiệm cận đứng và ngang của đồ thị hàm số y ax b mx n | ||
Thông hiểu: Tìm điều kiện của tham số để hàm số đạt cực trị tại x0 ; số cực trị của hàm số | ||
Thông hiểu: Tìm khoảng đồng biến, nghịch biến của một hàm số hoặc nhận dạng đồ thị hàm số qua chiều biến thiên của nó. | ||
Thông hiểu: Tìm GTLN của hàm số trên một đoạn | ||
Thông hiểu: Tìm điều kiện của các tham số để hàm số y ax b đồng biến, nghịch biến trên các khoảng xác định mx n của nó |
Vận dụng: Xác định tham số để hàm số bậc ba, bậc bốn trùng phương có điểm cực trị ,cực đại, cực tiểu thỏa mãn điều kiện cho trước có liên qua đến khoảng cách, tam giác | ||
Vận dụng: Tìm điều kiện của tham số để hàm số đồng biến, nghịch biến trên một khoảng hoặc Tìm điều kiện của tham số đề đồ thị hàm số và đường thẳng cắt nhau tại hai điểm phân biệt thỏa mãn điều kiện cho trước | ||
Vận dụng cao: Tìm điều kiện của tham số hàm số lượng giác có tham số đồng biến, nghịch biến trên một khoảng hoặc GTLN-GTNN, ứng dụng thực tế | ||
2. Hàm số luỹ thừa - hàm số mũ và hàm số lôgarit (10 câu) | Nhận biết: Định nghĩa, tính chất của lôgarit. Tính chất của hàm số lôgarit, đạo hàm của hàm số logarit | |
Nhận biết: Tính chất của hàm số mũ,đạo hàm của hàm số mũ, | ||
Nhận biết: Tính chất của hàm số lũy thừa, tập xác định của hàm số lũy thừa, đạo hàm của hàm số lũy thừa | ||
Nhận biết: Cách giải phương trình mũ cơ bản, phương trình lôgarit cơ bản | ||
Thông hiểu: Giải các phương trình mũ, lôgarit dạng thường gặp | ||
Thông hiểu: Sử dụng công thức mũ, logarit biến đổi các biểu thức mũ logarit | ||
Thông hiểu: Giải các bất phương trình mũ , logarit dạng thường gặp . Tìm tập xác định của hàm số hàm số logarit | ||
Thông hiểu: Đạo hàm, tính chất của hàm số mũ, logarit, lũy |