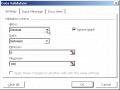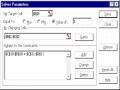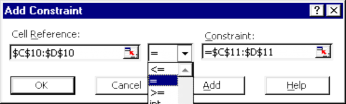
- Trong vùng [Subjects to the Constraints] ta nhập các ràng buộc dùng làm mục tiêu của lời giải. Đối với việc giải hệ phương trình, mục tiêu cần đạt được là các giá trị tạm phải bằng với các giá trị thực có (vế phải của các phương trình). Ở trước ta đã dùng ô B9 làm đích, vậy còn lại 2 giá trị phải đạt được. Ta chọn Add và khai báo đẳng thức còn lại làm mục tiêu trong hộp:
Sử dụng nút Add để thêm các ràng buộc, sau khi hoàn tất chọn [OK] để quay về hộp Solver Parameters
Bước 3. Thực hiện lệnh và kết thúc
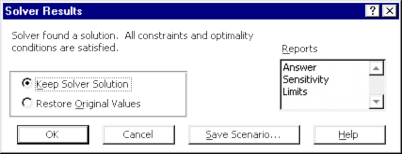
Sau khi hoàn tất các khai báo, ta chọn nút [Solve] để Excel tự động tính và thông báo kết quả;
Nếu đồng ý với lời giải thì chọn nút Keep Solver Solution, nếu không thì phục hồi các giá trị gốc Restore Orginal Values và chọn OK để hoàn tất.
Cuối cùng, ta có kết quả như sau:
A | B | C | D | |
1 | Biến | x | y | z |
2 | Nghiệm | 2 | 5 | 7 |
3 | ... | ... | ... | ... |
8 | ||||
9 | Giá trị | 5 | 40 | 78 |
10 | Mục tiêu | 5 | 40 | 78 |
Có thể bạn quan tâm!
-
Tin học văn phòng Microsoft Excel - Hoàng Vũ Luân - 7 -
Tin học văn phòng Microsoft Excel - Hoàng Vũ Luân - 8 -
Tin học văn phòng Microsoft Excel - Hoàng Vũ Luân - 9
Xem toàn bộ 83 trang tài liệu này.
Lưu ý rằng giá trị ở các ô B2:D2 và B9:D9 đã thay đổi.
Tóm lại, để sử dụng Solver đòi hỏi các yêu cầu sau:
- Phải cung cấp đầy đủ các tham số trong hộp thoại. Đặc biệt cần lưu ý rằng ô đích (Set Target Cell) cần phải chứa công thức có liên quan đến vùng nghiệm, nếu không Excel sẽ báo lỗi.
- Chỉ ra vùng mà Excel sẽ tác động và lưu kết quả, ở đây thường bắt đầu với các giá trị 1 là giá trị tạm thời để Excel có khởi điểm tính toán.
- Cung cấp đầy đủ các ràng buộc dùng làm mục tiêu để tính toán.
Bài tập tương tự. Giải hệ phương trình sau 3x + 4y - 3z - t = 26
4x - 2y + 6z - 7t = 10 {nghiệm là:
TIN HỌC ỨNG DỤNG - MICROSOFT EXCEL -
x + 4y + 8z - 6t = 12 (x=8; y=3; z=2; t=4) } 2x - 9y + 5z + 3t = 11
Bài 2. Xét bài toán tìm cực đại lợi nhuận như sau: “Một nhà máy sản xuất 3 sản phẩm (sph_a, sph_b và sph_c) với tiền lãi tương ứng trên 1 đơn vị sản phẩm là 75, 35 và 50. Các sản phẩm này đòi hỏi một số linh kiện (6 loại) với tương quan giữa chúng được cho bởi bảng và trong bảng còn cho biết số lượng các linh kiện tồn kho. Hãy lập kế hoạch sản xuất sao cho lợi nhuận thu được là lớn nhất.
Dùng Solver, ta lập mô hình bài toán như sau:
A | B | C | D | E | F | |
1 | SPh_a | SPh_b | SPh_c | |||
2 | Mục tiêu sản xuất -> | 100 | 100 | 100 | ||
3 | Linh kiện | Tồn kho | Yêu cầu | |||
4 | Lk_1 | 700 | 400 | 2 | 0 | 2 |
5 | Lk_2 | 850 | 500 | 3 | 0 | 2 |
6 | Lk_3 | 380 | 300 | 0 | 3 | 0 |
7 | Lk_4 | 500 | 400 | 2 | 1 | 1 |
8 | Lk_5 | 650 | 400 | 1 | 0 | 3 |
9 | Lk_6 | 450 | 200 | 0 | 1 | 1 |
10 | Tiền lãi/sp | 75 | 35 | 50 | ||
11 | Lợi nhuận | 7500 | 3500 | 5000 | ||
12 | Tổng lợi nhuận | 16000 | ||||
Trong mô hình trên, có các ô chứa công thức như sau:
- Các ô từ C4 đến C9 chứa hàm SumProduct($D$2:$F$2,D4:F4)...
- Tính lợi nhuận bằng tiền lãi một sản phẩm nhân với số sản phẩm
- Tổng lợi nhuận bằng tổng cộng các lợi nhuận của các sản phẩm.
Trong hộp thoại Solver Parameters ta khai báo như sau:
- Chọn ô D12 làm ô đích và giá trị mục tiêu là Max; các ô lưu kết quả là D2:F2 (với các giá trị khởi đầu là 100) và các ràng buộc như sau:
Sau khi chọn Solve, ta được nghiệm là 107, 105 và 181 với Tổng lợi nhuận là 20750.
Bài tập tương tự. Hãy thay đổi các tham số và giải lại bài toán trên. Hãy tìm một bài toán tương tự, (ví dụ lập lịch sản xuất sao cho chi phí thấp nhất) sau đó lập mô hình và giải.