Sử dụng phương pháp gần đúng khối lượng hiệu dụng nghiên cứu các trạng thái của electron trong chấm lượng tử

CHƯƠNG III TRẠNG THÁI ĐIỆN TỬ

TRONG CHẤM LƯỢNG TỬ

Xét các nano tinh thể lý tưởng hình cầu hoặc hình lập phương hay còn gọi là chấm lượng tử. Những loại như vậy không tồn tại trong tự nhiên. Sự mở rộng phương pháp gần đúng khối lượng hiệu dụng đối với các cấu trúc bị giam giữ không gian được dùng để giải bài toán “hạt trong hộp” và cung cấp một phương pháp để nghiên cứu các tính chất của tính thể nano.

3.1. Chế độ giam giữ yếu [8, 28 29]

Chế độ giam giữ yếu tương ứng với trường hợp khi bán kính chấm lượng tử a

là nhỏ nhưng vẫn lớn hơn so với bán kính Bohr

a B của exction. Trong trường hợp



Có thể bạn quan tâm!

Xem toàn bộ 61 trang tài liệu này.

22

này, xảy ra sự lượng tử hóa chuyển động khối tâm của exction. Xuất phát từ quy luật tán sắc của exction trong tinh thể nhưng thay thế động năng của exction tự do bằng nghiệm thu được với hạt trong hộp cầu. Năng lượng của exciton trong trường giam giữ yếu có biểu thức:

Enml

 Eg 

Ry* n2

2Ma2

(3.1)

với nghiệm của hàm cầu Bessel ml được trình bày thành bảng trong phần 1.2. Có thể thấy rằng, exction trong chấm lượng tử được đặc trưng bởi số lượng tử n mô tả các trạng thái bên trong của exction xuất hiện do tương tác Culông giữa lỗ trống và electron (1D, 2S, 2P, 3S, 3P, 3D, ....), và bởi hai số thêm vào là m và l mô tả các trạng thái liên quan đến chuyển động của khối tâm khi có mặt hàng rào thế bên ngoài ( 1s, 1p, 1d….. , 2s, 2p, 2d….,...). Các trạng thái bên trong và bên ngoài được phân biện bởi các chữ hoa và chữ thường.

Năng lượng ở trạng thái thấp nhất (n = 1, m = 0, l= 0) có biểu thức:

E1S1s

 E  Ry*

2 2

2Ma2

(3.2)

hay:

E  E



 Ry*  1

aB

2 



(3.3)

1S1s g

M a 



trong đó, là khối lượng rút gọn của electron và lỗ trống theo phương trình

e h

1 m*1  m*1 . Trong phương trình (3.2) và (3.3), giá trị

10  và các hệ thức

(2.4) và (2.6) đã được sử dụng. Do đó, cộng hưởng exction đầu tiên dịch về phía năng lượng cao một khoảng:

E 

aB

 Ry*

(3.4)

1S1s M a 

tuy nhiên, là nhỏ hơn so với



Ry* , nếu: a

(3.5)

Điều này chứng minh một cách đúng đắn cho thuật ngữ "giam giữ yếu"

Khi có tính đến sự hấp thụ photon có thể tạo ra một exction có mô men xung lượng bằng không thì phổ hấp thụ sẽ bao gồm một số vạch tương ứng các trạng thái với l = 0. Do đó, phổ hấp thụ có thể nhận được xuất phát từ phương trình (3.1) với

2Ma2 m

22

m0 m (xem phần 1.2) :

Enm  Eg 

Ry* 

( 3.1')

Electron tự do và lỗ trống có phổ năng lượng là:

E  E

ml g

2 2



2m a2

( 3.6 ')

h 22

Eml ml

2m a2

( 3.6 '')

Do đó, tổng năng lượng vượt quá ở trạng thái thấp nhất 1s của electron và lỗ trống là:

E  Ee

 Eh  E

22 

aB

 Ry*

(3.7 )

1s1s 1s 1s g

2a2

a 



cũng nhỏ hơn đáng kể so với Ry* . Chú ý đến mối quan hệ của các hệ thức (3.3) và

(3.6), xét hiệu giữa năng lượng tối thiểu cần thiết tạo ra các cặp electron – lỗ trống không liên kết:

Eeff  E

E

3.8

g g 1s1s

Và năng lượng tương ứng với sự cộng hưởng đầu tiên của exction (3.3) là

năng lượng liên kết hiệu dụng

Ryeff :



a

2 

Ryeff  Ry* 1 1

B

(3.9)

lớn hơn rất nhiều so với

Ry*



M  a



3.2. Chế độ giam giữ mạnh [8, 30 34]

Giới hạn giam giữ mạnh tương ứng với điều kiện :

(3.10)

Có nghĩa là electron và lỗ trống bị giam giữ không có trạng thái liên kết tương ứng với exction kiểu hiđrô, và động năng điểm không của electron và lỗ trống theo

công thức (3.6) khá lớn so với giá trị của Ry* . Trong trường hợp này, chuyển động

không tương quan của electron và lỗ trống có thể được coi là phép gần đúng bậc một và tương tác Coulomb có thể bỏ qua. Khi đó, mỗi hạt có phổ năng lượng được đưa ra bởi công thức (3.6). Phổ này được phác thảo trong hình 3.1.

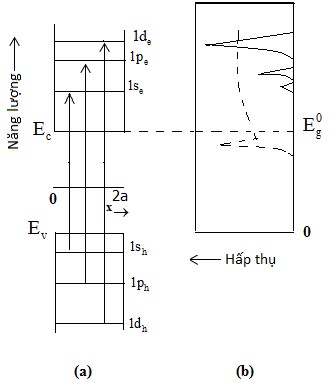
Hình 3.1: Các dịch chuyển quang học electron và lỗ trống trong mô hình không tương tác(a) và dạng phổ hấp thụ tương ứng (b).

2

Các định luật bảo toàn năng lượng và xung lượng dẫn đến quy tắc chọn lọc là các dịch chuyển quang học được phép là những dịch chuyển giữa các trạng thái của electron và lỗ trống có cùng lượng tử số chính và số lượng tử quỹ đạo. Do đó, phổ hấp thụ quy về một tập hợp các dải rời rạc có các đỉnh tại các giá trị năng lượng:

Enl

 Eg

 2a2 nl

(3.11)

Với suy luận này, các chấm lượng tử trong giới hạn giam giữ mạnh đôi khi được gọi là các nguyên tử nhân tạo hoặc siêu nguyên tử khi các chấm lượng tử có phổ quang học rời rạc và phổ quang học này được điều chỉnh bằng cách thay đổi kích thước chấm lượng tử (tức là số các nguyên tử), trong khi nguyên tử thực có phổ rời rạc được quy định bằng số lượng các nucleon.

Tuy nhiên, một electron và một lỗ trống bị giam giữ trong không gian có thể so sánh với kích thước của exction ở trạng thái cơ bản trong các tinh thể lí tưởng vô hạn. Do đó, sự nghiên cứu độc lập chuyển động của electron và lỗ trống là không hợp lí và phải tính đến toán tử Hamiltonian hai hạt với các số hạng động năng, năng lượng coulomb và thế giam giữ:

2 2 2 2 e2

H e h  U r 

(3.12)

2me

2mh

 re  rh

được nghiên cứu bởi Brus. Không giống như Hamiltonian kiểu hiđrô (1.34), sự xuất hiện của thế năng U(r) không cho phép nghiên cứu độc lập chuyển động của khối tâm và chuyển động của hạt với khối lượng rút gọn. Một số tác giả đã nghiên cứu vấn đề này bằng phương pháp biến phân (Brus 1986, Kayanuma 1986, Schmidt and Weller 1986 ) và nhận thấy rằng năng lượng của cặp electron - lỗ trống ở trạng thái cơ bản (1s1s) có thể được biểu diễn trong công thức :

2 2 e2

E1S1s  Eg 2a2 1, 786 a

(3.13)

trong đó số hạng tỷ lệ với a mô tả tương tác Culomb hiệu dụng của cặp lỗ trống

* e2

và electron. So sánh số hạng này với năng lượng Rydberg của exction

Ry 

2a

(công thức 2.6) và nhớ rằng vẫn đang xét giới hạn giam giữ mạnh (a << aB), có thể thấy rằng trong các chấm lượng tử tương tác culông không bị triệt tiêu. Hơn nữa, sự

đóng góp của số hạng này vào năng lượng ở trạng thái cơ bản thậm chí còn lớn hơn trong tinh thể khối. Đây là sự khác biệt chủ yếu của các chấm lượng tử so với tinh thể, giếng lượng tử và dây lượng tử, ở đó năng lượng Coulomb của cặp electron - lỗ trống tự do bằng không. Do đó, kích thích cơ bản trong chấm lượng tử có thể được gọi là exction với thuật ngữ “ exction trong chấm lượng tử ” (Banyai and Koch 1993; Woggon and Gaponenko 1995 ). Trong giới hạn này, chúng tôi sẽ sử dụng thuật ngữ exction ngay cả khi các trạng thái thích hợp không còn tuân theo mẫu

hiđrô. Năng lượng exction lệch khỏi năng lượng hạn giam mạnh có thể được:

Eg của bán dẫn khối trong giới

 a 2  a  a 2 

E  E

B

Ry*  A 

A 

A  ...

(3.14)

exc g

1

a B

aB 

với thông số a

1. Hệ số đầu tiên

A1 cho các trạng thái khác nhau được mô tả

bằng nghiệm của hàm cầu Bessel (xem công thức 3.6 và bảng 1.1). Hệ số thứ hai

A2 tương ứng với giới hạn Coulomb trong phương trình (2.13) và lấy các giá trị:

A2 1,786

với trạng thái 1S1s,

A2 1,884

với trạng thái 1P1p và có các giá trị từ

1, 6

đến

1,8

cho các dạng khác. Hệ số A3

cho trạng thái 1S1s được tìm thấy là:

A3  0, 248. Tóm lại, xét các trạng thái thích hợp của trạng thái cơ bản, chúng ta có thể viết năng lượng của đỉnh hấp thụ đầu tiên như sau :

E  E

2

aB

 Ry* 1,786aBRy* 0, 248Ry*

(3.15)

1S1s g a a



Sự phụ thuộc kích thước của năng lương hình 3.2.

E1S1s

vào kích thước được vẽ trong

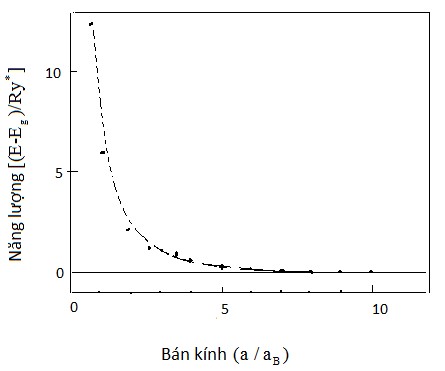
Hình 3.2: Sự phụ thuộc vào kích thước của năng lượng dịch chuyển quang học được phép đầu tiên trong chấm lượng tử lý tưởng được tính toán bởi Y.Kayanuma (1988) (các dấu chấm) và các phương trình gần đúng (3.15)(đường đứt dài) và phương trình (3.20) (đường đứt ngắn).

Trong đó, sử dụng các đơn vị năng lượng không thứ nguyên

Ry*

và chiều dài

a . Lưu ý rằng phương trình (3.15) là một hàm biểu diễn độ dịch của đỉnh hấp thụ

do giam giữ lượng tử dưới dạng không phụ thuộc vào các thông số vật liệu nếu

năng lượng được tính theo đơn vị

Ry *

và độ dài được đo theo đơn vị

aB .

ae ; ae ah aB ah

Có một số trường hợp nữa cho lời giải phương trình Schrodinger với thế giam giữ: Tương ứng với tỉ số rất lớn của khối lượng lỗ trống và electron, tức là:

với

mh me ; ah

(3.16)

2 2

ae m e2 ; ah m e2

( 3.17 )

e h

là bán kính Bohr của electron và lỗ trống. Trong trường hợp:

a ae , aB

lỗ trống có thể coi như không dịch chuyển và định xứ tại tâm của chấm.

(3.18)

Giả thuyết này là giống như phép gần đúng Born-Oppenheimer, và trạng thái electron - lỗ trống tương ứng trong chấm lượng tử bán dẫn được gọi là “exciton kiểu donor”(Efros và Efros 1982; Kayanuma 1988; Ekimov và cộng sự 1989). Trong mô hình này, các trạng thái năng lượng và quang phổ hấp thụ được xác định chủ yếu bởi sự lượng tử hóa chuyển động của electron [phương trình (3.6)]. Tuy nhiên, do tương tác Coulomb giữa electron và lỗ trống, mỗi mức electron bị tách thành nhiều mức con (Ekimov và cộng sự 1989). Vị trí của đỉnh hấp thụ cực đại đầu tiên có thể được mô tả bởi biểu thức (Kayanuma 1988).

 a 2

 2a 

E  E 8 Ry* exp 

l g

( 3.19 )



aB aB 

Trong giới hạn khối lượng rất lớn của lỗ trống, bài toán có liên quan đến exction bị giam giữ trong hộp có một số tính chất tương tự với bài toán có liên quan đến nguyên tử hiđrô trong hộp. Lý thuyết khác để giải quyết vấn đề này đã được đề cập đến bởi W.Jaskolski (1996). Nếu tính đến sự lượng tử hóa chuyển động khối tâm exciton hoặc lượng tử hóa chuyển động của lỗ trống và electron thì sẽ không đưa đến một hiệu ứng vật lý cơ bản hay sự gián đoạn khi kích thước chấm

vào khoảng

a aB . Sự có mặt của hiệu ứng kích thước lượng tử về chế độ giam yếu

và mạnh là rất hữu ích vì nó cung cấp cách giải quyết trực giác và các khuynh hướng dựa trên cơ sở của cơ học lượng tử cơ bản, và các khái niệm đã trình bày cho tinh thể vĩ mô là phù hợp khi áp dụng để nghiên cứu các tính chất của tinh thể nano. Trên thực tế, một sự phát triển thú vị các thuộc tính của chấm lượng tử từ tinh thể đến đám xuất hiện, và đã được chứng minh thành công trong khuôn khổ của phép gần đúng khối lượng hiệu dụng nhờ ý nghĩa của các nghiệm tường minh của phương trình Schrodinger với Hamilton (3.12). Bài toán này đã được thực hiện bởi một số tác giả (Kayanuma 1988; Mohan và Anderson 1989; Hu, Lindberg, và Koch 1990; Pollock và Koch 1991).

Phép phân tích bằng số kết quả có thể dự đoán các kết quả một cách trực giác trong khuôn khổ của cả chế độ giam giữ mạnh và yếu. Dịch chuyển đầu tiên phụ

thuộc vào kích thước cho thấy nó không nhạy với các giá trị tuyệt đối

me và mh và

tuân theo một quy luật phổ biến cho tất cả các chất bán dẫn khi dùng các đơn vị

không thứ nguyên của năng lượng và độ dài, tương tự như việc sử dụng rộng rãi các đơn vị nguyên tử.

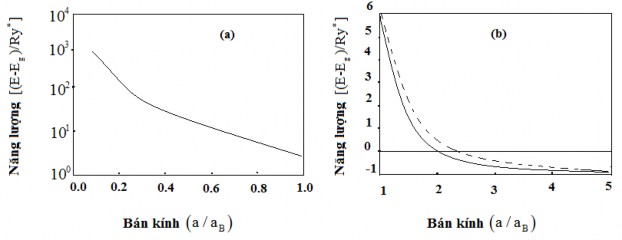
Hình 3.3: Sự phụ thuộc vào kích thước của năng lượng dịch chuyển quang học được phép đầu tiên khi tính đến tương tác Coulomb giữa điện tử và lỗ trống bằng phương pháp chéo hóa ma trận. Giá trị me/mh là 0,1 (đường nét liền) và 0,01(đường nét đứt).