Khái Niệm Các Giả Hạt: Electron, Lỗ Trống, Exction [8, 19  23]

CHƯƠNG II

KHÁI NIỆM CÁC GIẢ HẠT VÀ CÁC CẤU TRÚC THẤP CHIỀU

2.1. Khái niệm các giả hạt: electron, lỗ trống, exction [8, 19 23]

Các electron trong vùng dẫn của tinh thể có thể được mô tả như các hạt có

điện tích –e, spin 1/2, khối lượng m* (về cơ bản không phải là hằng số) và chuẩn

xung lượng k , với định luật bảo toàn riêng. Có thể thấy, trong các thông số trên, chỉ điển tích và spin là vẫn không thay đổi giá trị khi xét trong chân không và trong tinh thể. Do đó, khi nói về các electron trong vùng dẫn, ta hiểu đó là các hạt mà tính chất của chúng là do tương tác trong một hệ nhiều hạt bao gồm một số rất lớn các hạt nhân dương và các electron âm. Đó là cách tiếp cận thông thường trong lý thuyết về các hệ nhiều hạt, thay việc nghiên cứu một số rất lớn các hạt tương tác bởi một số nhỏ các giả hạt không tương tác. Các giả hạt này được mô tả như là các kích thích cơ bản của hệ gồm các hạt thực. Trong khuôn khổ cách tiếp cận này, electron trong vùng dẫn là một kích thích cơ bản của hệ trong tinh thể. Một kích thích cơ bản nữa là lỗ trống, là một giả hạt liên quan đến một tập hợp các electron trong vùng hóa trị bị thiếu một electron (ví dụ: chuyển lên vùng dẫn). Các kích

Có thể bạn quan tâm!

Xem toàn bộ 61 trang tài liệu này.

thích này được đặc trưng bởi điển tích +e, spin 1/2, khối lượng hiệu dụng* và

một chuẩn xung lượng thích hợp. Trong biểu diễn này, năng lượng của lỗ trống có dấu ngược với năng lượng của electron.

 Eg  Eekin  Ehkin

k  ke  kh

Sử dụng các khái niệm về kích thích cơ bản, có thể xem trạng thái cơ bản của tinh thể là một “trạng thái chân không” (không tồn tại electron trong vùng dẫn và cũng không tồn tại lỗ trống trong vùng hóa trị) và trạng thái bị kích thích đầu tiên (một electron trong vùng dẫn và một lỗ trống trong vùng hóa trị) chính là sự tạo thành của cặp electron - lỗ trống (cặp e – h). Sự dịch chuyển từ trạng thái cơ bản đến trạng thái kích thích đầu tiên xảy ra như là kết quả của một nhiễu loạn bên ngoài nào đó, ví dụ như sự hấp thụ photon (hình 2.1) với năng lượng và động năng được bảo toàn:

2.1

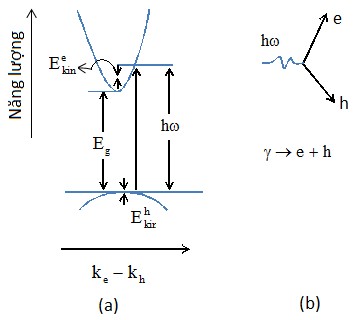
Hình 2.1: Quá trình hấp thụ một photon dẫn tới kết quả là tạo thành cặp electron - lỗ trống được minh họa bằng một dịch chuyển thẳng đứng (a ) thể hiện năng lượng và động lượng đồng thời được bảo toàn hoặc có thể được coi như là sự biến đổi một photon thành electron và lỗ trống (b).

Khi xung lượng photon là nhỏ không đáng kể, sự dịch chuyển là thẳng như trong hình 2.1 (a). Quá trình này có thể được mô tả theo một cách khác được trình bày trong hình 2.1 (b). Quá trình ngược lại, đó là quá trình dịch chuyển bức xạ xuống dưới, tương đương với sự hủy của cặp e - h và tạo ra một photon. Các quá trình và các khái niệm này cũng giống như trong chân không thực, các electron và pozitron (phản hạt). Sự khác biệt duy nhất là khối lượng pozitron đúng bằng khối

lượng electron

m0 , trong khi trong tinh thể, khối lượng hiệu dụng h

thường lớn

hơn khối lượng hiệu dụng của electron m* .

Là các fermion, các electron và lỗ trống được mô tả bởi thông kê Fermi – Dirac với hàm phân bố:

f E

E  EF

e kT 1

2.2

trong đó, EF

là thế năng hóa học và được gọi là năng lượng Fermi hoặc mức Fermi.

Năng lượng vùng cấm tương ứng với năng lượng tối thiểu tạo ra một cặp hạt mang điện tự do, đó là electron và lỗ trống. Sự trình bày này phù hợp với định

nghĩa của

Eg .

2m*

2 

2m*

 r  r

e h

Cách mô tả bằng các electron và lỗ trống không tương tác như là các kích thích cơ bản tương ứng với cái gọi là bức tranh một hạt. Trong thực tế, các electron và lỗ trống đều là các hạt tích điện nên có tương tác với nhau thông qua thế Coulomb và tạo nên một giả hạt đặc biệt tương ứng với trạng thái liên kết kiểu nguyên tử của cặp electron - lỗ trống và được gọi là exction. Tương tác giữa lỗ trống và electron được mô tả bởi toán tử Hamilton :

H 

2.3

nó giống như toán tử Hamilton (1.34) của nguyên tử hiđrô với

m* và m*

thay thế

e h

cho

m0 và M và với hằng số điện môi của tinh thể

1. Do đó, tương tự như

nguyên tử hiđrô, exction được đặc trưng bởi bán kính Bohr exction :

2 m o

aB 00,53A

2.4

e2 

trong đó là khối lượng rút gọn của cặp electron - lỗ trống:

e h

1 m*1  m*1

(2.5)

và năng lượng Rydberg exction là :

* e2

e4  1

Ry 

2a



B 0

22 2 m

2 13, 6 eV

2.6

Khối lượng rút gọn là nhỏ hơn khối lượng electron m0 và hằng số điện môi

lớn gấp vài lần so với chân không. Đây là lí do tại sao bán kính Bohr exction lớn hơn đáng kể còn năng lượng Rydberg exction nhỏ hơn đáng kể so với các giá trị

tương ứng của nguyên tử hiđrô. Các giá trị tuyệt đối của a B cho các chất bán dẫn

thông thường dao động trong khoảng 10 100 A và năng lượng Rydberg exction có giá trị trong khoảng 1 – 100 meV.

Một exction thực hiện dịch chuyển của khối tâm như là hạt không mang điện

e h

với khối lượng Mm*  m* . Mối quan hệ tán sắc có thể viết:

En k  Eg

 Ry 

2k2

n2 2M

2.7

Trong đó k là vectơ sóng exction. Phương trình (2.7) bao gồm tập hợp các mức năng lượng tương tự như nguyên tử hiđrô, động năng của chuyển động tịnh tiến, và năng lượng vùng cấm. Phổ năng lượng exction bao gồm các dải con (hình 2.2).

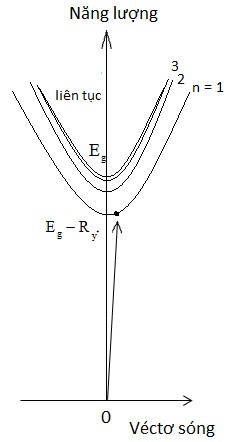
Hình 2.2: Đường cong tán sắc của một exciton và quá trình chuyển đổi quang học tương ứng để hấp thụ một photon và tạo exciton.

Tương tự như các cặp e – h tự do, exction có thể được tạo ra bằng cách hấp thụ photon. Nếu coi photon có xung lượng nhỏ không đáng kể thì sự tạo thành exction tương ứng với tập hợp rời rạc của năng lượng:

Ry*

En  Eg n2

2.8

Khí exction có thể được mô tả như khí Boson với hàm phân bố năng lượng tuân theo thông kê Bose – Einstein :

f E

E 

e kT 1

2.9

trong đó là thế hóa học. Với nhiệt độ T, mật độ exction nexc và của các electron

cũng như lỗ trống tự do

n  ne  nh

có liên hệ với nhau thông qua phương trình cân

bằng ion hóa hay phương trình Saha :

 2

2 m*  m* 3/2

Ry*

nexc

 n2 e h

kT m*m*

exp

2.10

e h 



Khi kT Ry* , đa số các exction bị ion hóa và các tính chất của hệ electron

của tinh thể được quyết định bởi các electron và lỗ trống tự do. Khi phần đáng kể các cặp e- h tồn tại trong trạng thái liên kết.

kTRy* , một

Do sự tạo thành các exction và các cặp e – h tự do, phổ hấp thụ của các đơn tinh thể bán dẫn có vùng cấm thẳng chứa đỉnh cộng hưởng năng lượng

 Eg  Ry , một tập hợp các đỉnh nhỏ hơn ở năng lượng En

(phương trình 2.8) và

hấp thụ trơn liên tục khi

 Eg (hình 2.3).

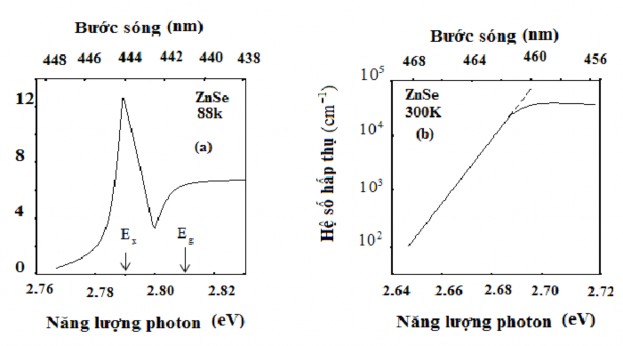
Hình 2.3: Phổ hấp thụ của đơn tinh thể ZnSe gần hấp thụ cơ bảnở nhiệt độ tương ứng với 88K (a) và 300K (b) (Gribkovskii và cộng sự. 1990).

2.2. Các cấu trúc thấp chiều: giếng lượng tử, dây lượng tử, chấm lượng tử [5]

Cấu trúc siêu mạng có độ dày các lớp bán dẫn kế tiếp nhau cỡ nanomet được gọi là cấu trúc nano. Bằng các kĩ thuật tinh vi trong việc nuôi tinh thể, người chúng ta đã tạo ra các cấu trúc nano có kích thước theo một chiều, hai chiều và thậm chí là ba chiều có thể so sánh với hoặc thậm chí nhỏ hơn bước sóng De Broglie của các kích thích cơ bản trong tinh thể hay bán kính Bohr của exciton, những cấu trúc này được gọi chung là các cấu trúc thấp chiều. Nếu kích thước của hệ bị hạn chế một chiều, chúng ta có hệ hai chiều (hệ 2D) hay giếng lượng tử, wellnano; nếu bị hạn chế hai chiều chúng ta có hệ một chiều (hệ 1D) hay dây lượng tử, wirenano; nếu bị hạn chế cả ba chiều chúng ta có hệ không chiều (hệ 0D) hay chấm lượng tử, dotnano. Trong vật liệu khối, hạt tải có ba bậc tự do nhưng khi kích thước của hệ bị giới hạn như trên thì hạt tải chỉ chuyển động tự do theo hai chiều (hệ 2D) hoặc một chiều (hệ 1D) và đặc biệt đối với hệ 0D hạt bị giam giữ theo mọi phương. Đặc điểm này tạo cho các hệ thấp chiều những tính chất khác thường mà ở bán dẫn khối không thể có được. Hai sự khác biệt có thể nhận thấy giữa các hệ thấp chiều so với vật liệu khối là có sự phân bố lại mật độ trạng thái và có sự biến đổi năng lượng của hạt tải.

Trong các hệ thấp chiều, mật độ trạng thái theo năng lượng của điện tử và lỗ trống có thể được biểu diễn dưới dạng chung như sau:

d -1

ρ(E)  E 2 với d = 1, 2, 3… (2.11)

Với d là số chiều và năng lượng E được xác định từ đáy vùng dẫn đối với điện tử và đỉnh vùng hoá trị đối với lỗ trống. Hàm mật độ trạng thái của điện tử và lỗ trống trong các hệ này được minh họa ở hình (2.4). Trong hệ 3D, ρ(E) là

hàm căn bậc hai trơn theo năng lượng nhưng với hệ 2D và 1D thì ρ(E) tách thành các dải con do hiệu ứng giam giữ lượng tử và mật độ trạng thái tuân theo (2.11) trong mỗi dải.

Về mặt năng lượng, trong các hệ thấp chiều, hạt tải có thêm năng lượng giam giữ do chuyển động bị giới hạn so với hệ ba chiều. Cụ thể, với hệ hai chiều có kích

thước bị giới hạn dọc theo trục z là lz

thì năng lượng lượng tử hoá theo trục z là:

2 π2 2

En = 2m*

l2 nz

(2.12)

e,h z

Với hệ một chiều, có thêm kích thước ly

bị giới hạn dọc theo trục y thì năng

lượng lượng tử hoá chuyển động hạt tải trong trường hợp này:

2 π2 n2 n2 

+ 

E =

y z



(2.13)

ny,z

2m*

l2 l2

e,h y z 

Vì có thêm năng lượng lượng tử hoá được cho bởi (2.12) và (2.13) nên phổ năng lượng của hệ 2D và 1D tách thành các dải con liên tục.

Còn riêng với hệ 0D, hệ này có các tính chất khác hẳn so với hệ 3D: Mật độ trạng thái là rời rạc giống hàm δ (H2.4c), phổ năng lượng là tập hợp các mức rời rạc giống với các mức năng lượng trong nguyên tử. Các tính chất này là nguyên nhân làm xuất hiện các hiệu ứng đặc biệt mà chỉ ở chấm lượng tử mới có.

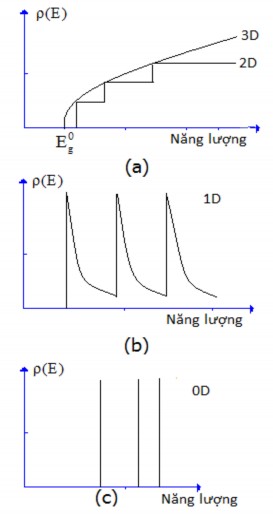
Hình 2.4: Mật độ của các trạng thái electron của giếng lượng tử (a), dây lượng tử (b), chấm lượng tử (c).

Theo lý thuyết vùng, năng lượng hạt tải tăng lên do giam giữ đồng nghĩa với việc đáy vùng dẫn dịch chuyển lên phía trên và đỉnh vùng hoá trị dịch chuyển xuống phía dưới, do đó làm tăng độ rộng vùng cấm hiệu dụng. Vì thế, trong các hệ thấp chiều, các dịch chuyển quang học được phép của hạt tải có thể được điều chỉnh bằng cách thay đổi kích thước của hệ.

Sau đây, chúng ta sẽ tìm hiểu về các trạng thái electron trong một tinh thể nano lý tưởng, đó là chấm lượng tử.