Các Mức Năng Lượng Của Một Hạt Trong Giếng Thế Hình Cầu Với Hàng Rào Vô

Hàm sóng bị tách thành các hàm của r, , :

 R r

và có thể được viết dưới dạng:

r,,un,l rY

(1.19)

,1.20

n,l ,m

r l,m

trong đó

Yl,m

là hàm cầu và

un,l r

thỏa mãn phương trình:

d u 



2 2 2

 U rl(l 1) u  Eu (1.21)

2m dr2  2mr2 



Khảo sát biểu thức (1.21) thay cho phương trình với toán tử Hamiltonian (1.17) thu được các giá trị năng lượng. Trạng thái của hệ được đặc trưng bởi ba lượng tử số, cụ thể là, số lượng tử chính n, số lượng tử quỹ đạo l, và số lượng tử từ

2l l 1

m. Số lượng tử quỹ đạo xác định giá trị mô men xung lượng L :

L2 

l  0, 1, 2, 3,...

1.22

Số lượng tử từ xác định thành phần của vectơ mô men xung lượng L trên trục oz:

Lz  m m 0, 1,  2,..., l

1.23

Mỗi trạng thái ứng với giá trị l nào đó thì bị suy biến bậc (2l +1) theo (2l + 1) giá trị của m. Các trạng thái tương ứng với các giá trị l khác nhau thường được ký hiệu là s, p, d, f, g… theo thứ tự bảng chữ cái. Ví dụ, trạng thái có mô men động lượng bằng không (l = 0) gọi là trạng thái s, trạng thái với l = 1 được kí hiệu là trạng thái p…Tính chẵn lẻ của trạng thái tương ứng với tính chẵn lẻ của giá trị l, vì

hàm bán kính không bị ảnh hưởng bởi phép nghịch đảo ( r vẫn không thay đổi sau phép nghịch đảo), còn hàm cầu sau phép nghịch đảo trở thành:

Yl,m

,1lY

,

(1.24)

l,m

Các giá trị cụ thể của năng lượng được xác định bởi hàm U (r). Xét trường hợp đơn giản tương ứng với giếng thế đối xứng hình cầu với hàng rào vô hạn:



Ux0 , x a

, x  a

(1.25)

trong trường hợp này, giá trị năng lượng được biểu diễn như sau:

Enl

2 2



2ma2

1.26

trong đó

nl

là nghiệm của hàm cầu Bessel với n là số thứ tự nghiệm và l là bậc

của hàm. Các giá trị của

nl

với một vài giá trị n, l được liệt kê trong bảng 1.1.

Bảng 1.1: Nghiệm của hàm cầu Bessel

nl

n = 1	n = 2	n =3
0	3,142 	6,283 2	9,425 3
1	4,493	7,725	10,904
2	5,764	9,095	12,323

Có thể bạn quan tâm!

Xem toàn bộ 61 trang tài liệu này.

Chú ý rằng với l = 0, những giá trị này bằng

n (n 1, 2, 3,...) và phương trình

(1.26) quy về biểu thức (1.7) trong trường hợp một chiều. Đó là khi l = 0, phương trình (1.21) với hàm bán kính u(r) chính là phương trình (1.4) với thế năng (1.3).

Tóm lại, hạt trong giếng thế hình cầu nhận tập hơp các mức năng lượng 1s, 2s, 3s, … trùng với năng lượng của hạt trong một giếng hình chữ nhật một chiều và các mức bổ sung 1p, 1d, 1f,…, 2p, 2d, 2f, …phát sinh do tính đối xứng cầu của giếng thế (hình 1.3).

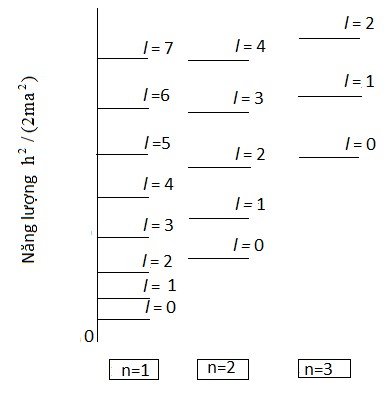
Hình 1.3: Các mức năng lượng của một hạt trong giếng thế hình cầu với hàng rào vô hạn.

Trong trường hợp của giếng hình cầu với thế năng hữu hạn

U0 . Phương trình

(1.26) có thể được áp dụng khi

U0 là đủ lớn, nghĩa là U0

. Vế phải của bất

8ma2

đẳng thức này là một hệ quả của hệ thức bất định (xem phương trình (1.11’)). Khi:

2 2

8ma2

U0  U0 min (1.27)

thì chỉ có một trạng thái tồn tại bên trong giếng thế,

E1  U0 . Khi

U0  U0 min ,

không có trạng thái nào tồn tại bên trong giếng. Đây là sự khác biệt quan trọng của trường hợp ba chiều khi so sánh với bài toán một chiều.

1.2.3. Electron trong thế Coulomb [8, 8 11]

Với thế Coulomb :

Ure

(1.28)

Phương trình ứng với thành phần xuyên tâm của hàm sóng có thể được viết:

 d2 2l l 1

 d2

U0

1.29



Với các biến số không thứ nguyên  và :

r ,

E

Trong đó a0

được cho bởi:

là đơn vị độ dài nguyên tử và E0

là đơn vị năng lượng nguyên tử

và :

a0  5, 292.102 nm m l 2

(1.30)

0 

E 2a2

13, 60 eV

(1.31)

với m0

là khối lượng của electron. Giải phương trình (1.29) dẫn đến các kết quả

Các mức năng lượng tuân theo dãy:

n

l 1n2

1.32

Các mức này được minh họa trong hình 1.4. Số

n nr l 1

được gọi là “số

lượng tử chính”. Nó lấy các giá trị nguyên dương bắt đầu từ 1. Năng lượng được

xác định hoàn toàn bởi giá trị đã cho của n, nr

xác định số lượng tử các nút của

hàm sóng tương ứng. Nó được gọi là “số lượng tử quỹ đạo”. Ứng với mỗi giá trị

của n có n giá trị của l (l chạy từ

0n 1). Thêm vào đó, ứng với mỗi giá trị l đã

cho, có (2l +1 ) suy biến xảy xa đối với m  0, 1,  2, .... Do đó, tổng bậc suy biến là:

n 1

2l 1  n2

l  0

(1.33)

Cho n = 1, l = 0 (trạng thái 1s), hàm sóng tuân theo đối xứng cầu với a0 là

khoảng cách ngắn nhất có thể tìm thấy electron với xác suất lớn nhất. Do vậy, giá

trị này trong kiểu cấu trúc nguyên tử được gọi là “bán kính Bohr”. Khi E > 0, hạt chuyển động không giới nội với phổ liên tục.

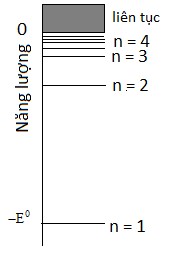
Hình 1.4: Mức năng lượng của một hạt trong thế Coulomb

Ur e2

r . Với

E > 0, hạt có phổ năng lượng liên tục. Với E < 0, phổ năng lượng bao gồm một tập

hợp rời rạc của các mức tuân theo các mối quan hệ

En  E

n2 , mỗi mức có bậc

suy biến n 2 .

Sau đây, xét bài toán nguyên tử hiđrô bao gồm một proton có khối lượng

M0 và một electron khối lượng m0 . Phương trình Schrodinger có liên quan là

phương trình hai hạt với toán tử Hamilton:

2 

r  r

p e

H 

1.34

Trong đó rp , re lần lượt là bán kính vectơ của proton và electron, còn chỉ số p

và e trong toán tử 2 biểu thị phép lấy vi phân theo tọa độ proton và electron.

Xét bán kính vectơ tương đối r và bán kính vectơ xác định vị trí khối tâm R

như sau :

r  rp  re , R m0 re  m0 rp

m0  M0

và sử dụng khối lượng tổng cộng M và khối lượng rút gọn của hệ:

1.35

M  m

 M , 

m0M0

1.36

0 0 m

0  M0

Toán tử Hamilton (1.34) trở thành:

H 

2 

2m0

2m0 r

1.37

có thể thấy rằng (1.37) được phân tích thành toán tử Hamilton của hạt tự do với khối lượng M và toán tử Hamilton của hạt với khối lượng rút gọn chuyển động

U r

trong thế Coulomb e2 . Toán tử Hamilton thứ nhất mô tả chuyển động tự do

của khối tâm nguyên tử, toán tử Hamilton thứ hai làm xuất hiện các trạng thái bên trong. Theo (1.32), năng lượng của các trạng thái này có thể được viết:

với :

En n2

e2 2

1.38

R y 2a , aB e2

1.39

ở đây,

R y được gọi là “ hằng số Rydberg” và là năng lượng ion hóa của trạng thái

thấp nhất, còn aB

là bán kính Bohr của nguyên tử hiđrô.

Khoảng cách giữa các mức năng lượng kế tiếp giảm theo n và khi E > 0, electron và proton chuyển động không giới nội.

Ta thấy năng lượng và bán kính Bohr thể hiện qua (1.39) khác với các giá trị

tương ứng của bài toán một hạt đơn giản bởi hệ số

(1.31) được sử dụng rộng rãi thay cho (1.39).

. Do đó, biểu thức (1.30 ) và

Các bài toán hạt trong giếng cầu và của nguyên tử hiđrô là rất quan trọng cho các nghiên cứu tiếp theo. Bài toán về hạt trong giếng thế cầu được sử dụng cho mô hình electron và lỗ trống trong tinh thể nano còn bài toán nguyên tử hiđrô là bài toán cơ bản cho exciton trong tinh thể khối cũng như trong các tinh thể nano. Hơn nữa, ví dụ về bài toán hai hạt là cơ sở cho bài toán nhiều vật. Nó bao gồm sự chuyển tiếp từ bài toán nhiều hạt (proton và electron) thành bài toán một hạt bằng

cách tái chuẩn hóa khối lượng (khối lượng rút gọn thay bằng M0 và m0 ) và tách

chuyển động tập thể thành chuyển động tịnh tiến của khối tâm và chuyển động của

hạt đơn lẻ trong một trường hiệu dụng nào đó. Cách tiếp cận này dẫn đến các khái niệm khối lượng hiệu dụng và các giả hạt được giới thiệu trong phần sau.

1.2.4. Hạt trong thế tuần hoàn [8,11 15]

Xét hạt trong trường thế thỏa mãn :

Ux Ux a1.40

Tìm hàm sóng thỏa mãn các phương trình Schrodinger với thế năng (1.40).

Nếu đối số x được thay thế bằng x +a :

x x a

Ta được phương trình :

2x  a  U x x  a  E x  a 1.41

So sánh (1.41) và (1.4) thì hàm sóng

x  avà

x

đều thỏa mãn phương

trình Schrodinger với cùng một trị riêng E. Nếu trị riêng này không suy biến (tức là

chỉ có l hàm riêng), thì hàm

xvà

x  akhác nhau một hằng số c nào đó:

x acx1.42

Cả hai hàm riêng phải thỏa mãn điều kiện chuẩn hóa, giá trị tuyệt đối của c là :

c 1

Do đó :

x  a 2 x 2

1.43

Phương trình này cho thấy, hạt có thể tìm thấy trong khoảng x quanh điểm x

có cùng xác suất như quanh điểm x  a . Do đó, sự phân bố trung bình trong không

gian của các hạt có tính chất tuần hoàn của thế năng. Khảo sát các tính chất của giá

trị

c0 . Sau khi thực hiện hai lần phép tịnh tiến, ta được :

xan1 an2 cn1cn2x1.42'

Trong đó:

an  na, n  1, 2, 3,...

Hiển nhiên, ta có:

an1 an2 an1 n2

Ta thấy :

Do đó:

x  an1  an 2 x  an1 n 2  cn1 n 2x

ika

cn1cn 2 cn1 n 2

(1.42'')

1.44

Phương trình này có nghiệm :

trong đó k có thể lấy nhiều giá trị.

cn e n

1.45

Tóm lại, các hàm sóng thỏa mãn phương trình Schrodinger với thế tuần

hoàn chỉ khác hàm tuần hoàn với chu kỳ a một hệ số có dạng hàm tuyến tính của x. Như vậy, hàm sóng có thể viết:

eif x, trong đó f(x ) là

k k k n

xeikx ux, u x u xa 

(1.46)

Phương trình (1.46) cho thấy các hàm riêng của Hamilton với thế năng tuần hoàn là một sóng phẳng biến đổi tuần hoàn cùng chu kì với thế năng. Phát biểu này là định lí Bloch.

Vectơ sóng

k1, k2

khác nhau bởi giá trị:

k1  k2 2 n , n 1,  2,  3,... a

1.47

trở nên tương đương. Đây là hệ quả trực tiếp của tính đối xứng tịnh tiến của không gian. Do đó, tập hợp vô số các giá trị k bao gồm các khoảng tương đương :

	 k 	;	 k 	3; 3	 k 	5
a		a a		a a		a

 ;...

1.48

với độ rộng của mỗi vùng là 2 . Mỗi khoảng này có chứa một tập hợp đầy đủ các

giá trị không tương đương của k và được gọi là “vùng Brillouin”. Phổ năng lượng và đường cong tán sắc khác với trường hợp hạt tự do (hình 1.5).