Sử dụng phương pháp gần đúng khối lượng hiệu dụng nghiên cứu các trạng thái của electron trong chấm lượng tử

NỘI DUNG

CHƯƠNG I

PHƯƠNG PHÁP GẦN ĐÚNG KHỐI LƯỢNG HIỆU DỤNG CHO BÀI TOÁN ELETRON TRONG TINH THỂ

1.1. Giới thiệu các phương pháp gần đúng nghiên cứu chuyển động của electron trong tinh thể [4, 77 78]

Việc nghiên cứu tính chất của electron trong tinh thể là một trong những nhiệm vụ quan trọng nhất của vật lý chất rắn. Đó là vì electron là hạt có khối lượng bé, mang điện tích nguyên tố âm nên là hạt rất linh động, tham gia vào nhiều hiện tượng quy định nhiều tính chất của vật chất. Đây là một vấn đề khó vì rằng để mô tả chính xác tính chất của electron trong tinh thể cần phải xét một hệ gồm rất nhiều hạt tương tác với nhau : electron và hạt nhân. Số lượng số hạt này rất lớn, cùng bậc

với số Avôgađrô ( 6.1023 ) nên khi tính toán ta phải lập và giải một hệ phương

trình rất lớn đến mức các máy tính hiện đại mạnh nhất hiện nay cũng không giải được.

Vì vậy cần tìm cách đơn giản hóa các phép tính toán bằng cách sử dụng các phép gần đúng.

Trong tinh thể vật rắn, các nguyên tử cấu tạo nên hệ tương tác với nhau. Electron trong từng nguyên tử của tinh thể chịu tác dụng của tương tác giữa các nguyên tử. Electron ở lớp ngoài cùng chịu ảnh hưởng rất yếu của hạt nhân và dễ bứt ra chuyển động tự do trong mạng tinh thể gọi là các electron hóa trị. Khi nghiên cứu tính chất của vật rắn ta chỉ giới hạn việc khảo sát tính chất của các electron hóa trị. Theo đó, ta coi mạng tinh thể được cấu tạo từ các lõi nguyên tử (gồm hạt nhân và những electron ở lớp bên trong) mang điện dương, đặt ở các nút mạng và các electron hóa trị.

Có thể bạn quan tâm!

Xem toàn bộ 61 trang tài liệu này.

Đầu tiên ta giả thiết rằng các lõi nguyên tử đứng yên đối với các nút mạng, xếp đặt tuần hoàn trong mạng tinh thể. Với giả thiết này, ta xét chuyển động của electron trong trường lực của các lõi nguyên tử đứng yên, xếp đặt tuần hoàn trong mạng tinh thể. Sau đó mới tiếp tục xét đến ảnh hưởng của dao động mạng lên tính chất electron.

Tuy nhiên, với giả thiết trên bài toán vẫn còn phức tạp vì ta vẫn phải xét

khoảng

1023

electron tương tác với electron. Vì vậy một phép gần đúng đơn giản

hóa tiếp theo là sử dụng phép gần đúng một electron. Theo cách này, ta giả thiết rằng có thể xét chuyển động của từng electron hóa trị riêng rẽ trong một trường thế

Vr

nào đó phụ thuộc vào bản thân electron mà ta đang xét, trường này được gây

ra bởi tất cả các electron còn lại cùng với tất cả các lõi nguyên tử trong tinh thể.

Sau đó, tùy thuộc vào ảnh hưởng của trường thế

Vr

lên chuyển động của

electron mà ta có các mô hình khác nhau cho tinh thể. Điều này cũng dẫn tới các cách tiếp cận khác nhau khi nghiên cứu chuyển động của electron trong tinh thể thể hiện qua các phương pháp gần đúng như phương pháp gần đúng electron liên kết yếu, phương pháp gần đúng electron liên kết mạnh, phương pháp LCAO…

1.1.1. Phương pháp gần đúng electron liên kết yếu [4, 93]

Trong phương pháp này ta xét bài toán về chuyển động của electron trong

trường hợp thế năng Vrcủa electron là yếu. Hay nói cách khác, electron liên kết

yếu với các ion nút mạng. Do thế năng

Vr

là yếu nên ta có thể coi nó là một nhiễu

loạn và áp dụng lý thuyết nhiễu loạn của cơ học lượng tử để giải bài toán này.

Trên cơ sở của phép gần đúng này, ta có thể giải thích được nhiều tính chất chung của vùng năng lượng trong vật rắn và giải quyết nhiều bài toán về electron trong kim loại.

Phương pháp này áp dụng tốt cho electron lớp ngoài cùng vì những electron này chịu tác dụng rất yếu của các lõi nguyên tử. Tuy nhiên, phương pháp này có nhược điểm là mới xét hàm sóng ở xa tâm ion được coi gần như sóng phẳng nhưng chưa tính đến hàm sóng của electron ở gần tâm ion có dao động nhanh như hàm nguyên tử.

1.1.2. Phương pháp gần đúng electron liên kết mạnh [4, 105 112]

Đối với các tinh thể trong đó electron liên kết chặt với lõi nguyên tử thì trạng thái của electron gần với trạng thái nguyên tử hơn là trạng thái electron tự do. Trong trường hợp này, ta sử dụng phương pháp electron kết mạnh. Ở đây hàm sóng của electron được xây dựng dưới dạng tổ hợp tuyến tính của các hàm nguyên tử. Mỗi trạng thái nguyên tử này định xứ tại một nguyên tử nhất định nhưng trạng thái thông qua tổ hợp các hàm nguyên tử được lan truyền trong toàn tinh thể. Phương pháp này mô tả một nguyên lý quan trọng. Giả sử có N nguyên tử đặt rất xa nhau, khi tổ hợp lại sẽ xuất hiện trạng thái suy biến bậc N đối với mỗi electron riêng biệt.

Khi các nguyên tử trên xích lại gần thì các hàm sóng sẽ phủ lẫn nhau và các trạng thái trước đây suy biến bậc N sẽ tách ra thành các vùng, mỗi mức nguyên tử ứng với một vùng gồm N trạng thái.

Phương pháp electron liên kết mạnh thích hợp cho việc nghiên cứu tính chất của các electron ở những lớp bên trong của tinh thể. Phương pháp này có thể giải thích được sự hình thành vùng năng lượng vật rắn và cho thấy chỉ cần sự ảnh hưởng lẫn nhau giữa các nguyên tử lân cận là đã đủ làm sinh ra bức tranh vùng năng lượng chứ không phải chỉ có tính tuần hoàn của trường tinh thể. Do đó, một số chất rắn không có cấu trúc tinh thể vẫn có thể có các vùng năng lượng.

1.1.3. Phương pháp tổ hợp tuyến tính các hàm nguyên tử [3, 137 138]

Các vùng khác nhau nêu trên có thể rộng đến mức bắt đầu phủ nhau. Khi đó phương pháp gần đúng electron liên kết mạnh phải được biến đổi và hàm sóng của hệ là tổ hợp tuyến tính của các hàm nguyên tử (Linear Canbination of Atomic Orbitals). Phương pháp LCAO được sử dụng rộng rãi trong hóa lượng tử để xác định các hàm sóng của các phân tử. Tuy nhiên nó không được thành công lắm đối với tính giải tích các hàm Bloch trong vật rắn. Lý do không những ở khối lượng tính lớn hay các hàm cơ sở không trực giao mà còn ở những điều không thích hợp mà ta không xét ở đây.

1.1.4. Phương pháp giả thế [3, 146 148]

Phương pháp này thay thế năng lượng của từng nguyên tử riêng biệt

Va bằng

một thế yếu

Wa . Trừ đi các hàm sóng chuẩn hóa của các trạng thái bên trong tâm

lõi nguyên tử, giả thế yếu

Wa cần được xây dựng sao cho ở ngoài vùng tâm lõi của

nguyên tử nó dẫn đến chính xác các hàm sóng mà chúng ứng với thế nguyên tử

Va .

Phương pháp này đưa đến khả năng giải quyết trong toàn bộ vấn đề của lý thuyết về cấu trúc vùng. Tuy nhiên, việc làm trên gặp phải một số khó khăn do tính không định xứ và không đơn giá cũng như sự phụ thuộc vào năng lượng của giả thế.

1.1.5. Phương pháp gần đúng khối lượng hiệu dụng [4, 126 129]

Theo cơ học lượng tử, mọi thông tin về tính chất của các hệ vật lí được bao gồm trong phương trình Schrodinger. Đối với electron trong tinh thể, hàm sóng của nó là nghiệm của phương trình Schrodinger có dạng:



2

 2m

2 V rr E r 

(1.1)

với

Vr



là thế năng của electron trong trường tuần hoàn của tinh thể,

r

là hàm



sóng của electron, E là năng lượng của electron. Giải phương trình này rất khó vì ta

không thể biết chính xác biểu thức thế năng Vr.

Bằng cách đưa vào khái niệm khối lượng hiệu dụng m*, ta thấy rằng khi xác định năng lượng của electron trong tinh thể thì ở gần điểm cực trị, ta có thể thay phương trình Schrodinger trong trường tuần hoàn bằng phương trình Schrodinger cho hạt tự do với khối lượng thực m của electron được thay bằng khối lượng hiệu dụng m*. Khi đó phương trình Schrodinger có dạng đơn giản:

 r 

2m*



E r



(1.2)

Khi có một trường lực ngoài biến đổi chậm trong không gian tác dụng lên tinh

thể thì electron trong tinh thể chịu tác dụng của thế Vrvà thế U của lực ngoài.

Bằng cách dùng khối lượng hiệu dụng thay cho tác động của trường tinh thể

Vr,

phương trình Schrodinger hoàn toàn giải được khi ta luôn biết được biểu thức trường ngoài U.

Phương pháp nghiên cứu như vậy gọi là phương pháp gần đúng khối lượng hiệu dụng. Đây là phương pháp gần đúng có rất nhiều ưu điểm đã được áp dụng thành công trong vật lý chất rắn. Đặc biệt, phương pháp này được sử dụng rộng rãi khi nghiên cứu các vật liệu bán dẫn. Khái niệm khối lượng hiệu dụng sẽ được trình bày kĩ ở phần sau.

1.2. Electron trong tinh thể và khái niệm khối lượng hiệu dụng

1.2.1. Hạt trong giếng thế [8, 1 4]

Xét một hạt có khối lượng m, chuyển động trong một giếng thế vuông góc với bờ thế cao vô hạn:

Ux

0 , x



, x

 a 2



(1.3)

Phương trình Schrodinger độc lập với thời gian có thể viết:

2 2

x U xx Ex 

(1.4)

2m x2

Theo cơ học lượng tử, phương trình (1.4) có hai loại nghiệm chẵn và lẻ được cho bởi biểu thức:



cos 1

2mE

n 1, 3, 5,...

(1.5)

và



sin

n  2, 4, 6,...

(1.6)

1 2mE

2 2n2

2ma2

Kết quả quan trọng nhất của bài toán là một tập hợp các giá trị năng lượng:

En 

1.7

Hình (1.1a) minh họa 3 hàm sóng đầu tiên ứng với n = 1, 2, 3 và vị trí các mức năng lượng tương ứng.

Khoảng cách giữa hai mức năng lượng kế tiếp:

2

2 ( 2n 1)

2ma2



En  En 1  En 

(1.8)

tăng đơn điệu theo n. Hàm sóng với mọi trạng thái bị triệt tiêu tại x . Biên độ

của tất cả các hàm số sóng đều như nhau và tổng xác suất tìm thấy một hạt bên trong giếng đúng bằng một đơn vị cho tất cả các trạng thái.

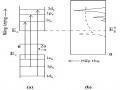
(a) (b) (c)

Hình 1.1: Giếng thế một chiều có hàng rào vô hạn (a) và hữu hạn (b) ứng với ba trạng thái đầu tiên và quy luật tán sắc của giếng thế có hàng rào hữu hạn (c).

Chú ý rằng năng lượng trong phương trình (1.7) ứng với giá trị động năng. Sử dụng mối quan hệ giữa năng lượng E, xung lượng p và vectơ sóng k

p  k

E 1.9

Ta được giá trị của xung lượng p và vectơ sóng k :

cũng là các giá trị rời rạc.

p  n

n a

, kn

n

(1.10)

Nếu một hạt tồn tại trong giếng, giá trị * tại một vị trí nào đó phải khác

không. Các nghiệm thỏa mãn (1.3) và (1.4) với n = 0 là không được phép vì sẽ phủ nhận sự tồn tại của hạt. Năng lượng nhỏ nhất của hạt:

2 2

E1  2m a2

(1.11)

Năng lượng này được gọi là năng lượng điểm không của hạt. Kết quả này còn có thể suy ra từ hệ thức bất định Heisenberg:

p x 

(1.12)

Hạt bị giới hạn trong miền không gian x  a . Do đó, theo (1.12), độ bất định

của động lượng p . Kết quả này cho phép tìm được năng lượng nhỏ nhất:

p2 2

E 



8ma2

1.11'

Kết quả này tương tự

E1 trong (1.11) với độ chính xác là 4

Tính chẵn lẻ của hàm sóng hạt có thể được dự đoán từ tính đối xứng của bài toán. Tính đối xứng của giếng thế :

Ux Ux

xác định tính đối xứng của mật độ hạt:

x 2 x 2

Từ đó :

xx

(1.13)

là hai nghiệm độc lập. Nói chung, tính đối xứng của các hàm sóng thường thuận lợi trong việc giải quyết các phương trình sóng cho một hệ phức tạp.

Trong trường hợp hàng rào thế có chiều cao hữu hạn, hàm sóng không triệt tiêu ở bờ giếng nhưng giảm theo quy luật hàm mũ trong khu vực cấm cổ điển

x a

[hình.1.1 (b)]. Xác suất tìm một hạt bên ngoài giếng là khác không, xác suất

này tăng khi n tăng. Số lượng các trạng thái bên trong giếng tuân theo điều kiện:

2mU0

n 1

a 

(1.14)

Trong đó,

U0 là chiều cao của giếng. Điều kiện này luôn thỏa mãn với n = 1.

Do đó, luôn có ít nhất một trạng thái trong giếng thế với một tổ hợp bất kỳ của U0

và a. Số lượng các trạng thái trong giếng có thể có ứng với giá trị lớn nhất của n mà (1.14) vẫn được thỏa mãn. Với các trạng thái sâu, phương trình (1.7) có thể được

coi như là một phép gần đúng tốt. Tất cả các trạng thái với

En  U0 ứng với chuyển

động không giới nội và tạo nên tính liên tục của các trạng thái.

1.2.2. Hạt trong thế đối xứng cầu [8, 5 7]

Trong trường hợp này, toán tử Hamilton của hạt có dạng :

trong đó r 

, :

H 2  Ur1.15

x2  y2  z2

. Từ tính đối xứng của bài toán, xét trong hệ tọa độ cầu, r,

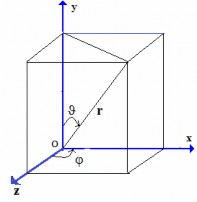
Hình 1.2: Hệ tọa độ cầu

x rsin cos, y  rsin sin , z  r cos

Khi đó, phương trình Hamiltomain có dạng:

2 

2mr 

r 





r 2mr







2 A



U r



H 

(1.16)

1.17

trong đó, toán tử A :

1  1 2 

2 

A  sin 

sin  sin 

1.18

