Để tìm các mục phổ biến đóng còn lại có chứa a nhưng không d, chúng ta cần phải tiếp tục khai thác TDB|a. Đầu tiên, tập các mục phổ biến trong TDB|a, f_lista =
{c: 2; e: 2; f: 2}3. Theo f_lista, các tập phổ biến đóng có chứa a nhưng không d có thể được phân chia thêm thành ba tập con:
(1) Tập con có chứa af nhưng không d,
(2) Tập con có chứa ae nhưng không chứa d hoặc f,
(3) Tập con có chứa ac nhưng d, e hoặc f.
Chúng có thể được khai thác bằng cách xây dựng cơ sở dữ liệu có điều kiện đệ quy. Độ phổ biến fa tương đương với cfad, do đó fa và a cũng là một hạng mục phổ biến đóng được tìm thấy. Điều đó có nghĩa là mọi giao tác có chứa fa cũng phải chứa cfad. Do đó, không có mục phổ biến đóng có chứa fa nhưng không có d. Tương tự như vậy, không có mục phổ biến đóng chứa ca không d, e hoặc f, vì ca là một tập con của cfad và sup (ca) = sup (cfad). Cơ sở dữ liệu có điều kiện ea, TDB|e a = {c}, không thể tạo ra bất kỳ mục phổ biến nào. Vì vậy, ea: 2 là tập phổ biến đóng.
(c) Tìm các tập phổ biến đóng chứa f nhưng không có d. TDB|f = {ce: 3; c}, c xuất hiện trong mọi giao tác f-cond, và cf không phải là tập hợp con của bất kỳ tập phổ biến đóng nào có cùng sự phổ biến, do đó cf: 4 là một tập phổ biến đóng. Độ phổ biến của fc bằng với f và c, f và c luôn xuất hiện cùng nhau, do đó không có các tập phổ biến đóng chứa c nhưng không có f. Ngoài ra, cef: 3 không phải là tập hợp con của bất kỳ mục nào được tìm thấy, do đó, nó là một tập phổ biến đóng.
(d) Tìm các phổ biến đóng chứa e nhưng không có f, a và d. Tương tự, TDB|e
= {c: 3}. Nhưng ce không phải là một tập đóng vì nó là một tập con của cef và sup(ce)
= sup(cef). Tuy nhiên, e: 4 là một tập phổ biến đóng.
(e) Tìm các tập phổ biến đóng chỉ chứa c. Chúng ta biết rằng không có các tập phổ biến đóng chỉ có chứa c nhưng không có f, do đó không có các tập phổ biến đóng chỉ chứa c.
4. Tóm lại, tập hợp các tập phổ biến đóng được tìm thấy là {acdf: 2, a: 3, ae: 2, cf: 4, cef: 3, e: 4}
Đánh giá: Mặc dù CLOSET sử dụng một số kỹ thuật tối ưu hóa để nâng cao hiệu quả hoạt động khai thác, hiệu quả của nó vẫn chưa cao trong bộ dữ liệu thưa thớt hoặc khi ngưỡng phổ biến thấp.
2.3.4. Thuật toán BitTableFI
Thuật toán BitTableFI [10] sử dụng kỹ thuật nén tập dữ liệu dựa trên cấu trúc BitTable. Theo cách nén này, dữ liệu được bố trí dưới dạng dãy các bit, mỗi một tập mục sẽ chiếm |T| bit. Vì vậy, mỗi tập mục sẽ chiếm |T|/8 + 1 byte. Khi tạo ra một tập mục mới XY từ hai tập mục X và Y, Bitlist của XY sẽ được tính dựa trên Bitlist của các tập mục có trong XY bằng cách lấy phần giao giữa các byte có trong các Bitlist. Do lực lượng của hai vectơ bit là bằng nhau nên kết quả sẽ cho ra một vectơ bit (Bitlist) có chiều dài là |T|/8 + 1 byte. Thuật toán khai thác tập phổ biến theo cấu trúc này được các tác giả tiếp cận dựa vào nguyên lý Apriori [3]. Điểm khác biệt chính là cách tính độ phổ biến: thuật toán Apriori tính độ phổ biến bằng cách quét lại CSDL, còn BitTableFI chỉ cần tính phần giao trên các vectơ bit. Độ phổ biến của hạng mụcset kết quả có thể được tính nhanh dựa vào số bit 1 có trong vectơ bit. Thuật toán Index- BitTableFI được nhóm tác giả Wei-Song đề xuất để cải tiến BitTableFI. Các tác giả dựa vào khái niệm subsume để gộp các tập mục. Cách gộp như sau: đầu tiên, sắp xếp các tập mục tăng theo độ phổ biến, xét mỗi tập mục i với các tập mục đứng sau nó (theo thứ tự đã sắp xếp), nếu Bitlist i là con của Bitlist j thì j thuộc về tập subsume của i. Việc tạo ra subsume và khai thác tập phổ biến dựa trên subsume cải tiến đáng kể thời gian khai thác tập phổ biến.
2.3.5. Thuật toán PIETM
Một thuật toán khai thác tập phổ biến dựa trên nguyên lý Bao gồm - Loại trừ và ánh xạ giao tác. Kiến trúc cơ bản của thuật toán PIETM [16] tuân theo chiến lược khai thác của Apriori [3]. Không quét cơ sở dữ liệu để đếm độ phổ biến của các tập mục, PIETM xây dựng một cấu trúc cây, lưu đầy đủ thông tin cho việc khai thác các tập phổ biến. Nguyên tắc bao gồm – Loại trừ được sử dụng để tích hợp cấu trúc cây với chiến lược từ dưới lên. Mặc dù PIETM kết hợp chiến lược khai thác của Apriori và cấu trúc cây FP-Growth [4], PIETM đã loại bỏ điểm yếu của hai thuật toán bằng cách kết hợp các tính năng chính của Apriori, FP-Growth và PIETM như hình
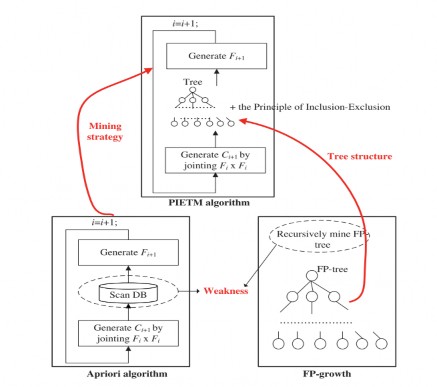
Hình 2.15 Thuật toán Apriori, FP-Growth và PIETM
Thuật toán PIETM Input:
Output:
1: Tree=Build_Tree(DB, minsup)
2: mapTransaction_Intervals(Tree) 3: for (k=2; Ck!=0; k++) do
4: Generate candidate k-itemsets into Ck by joining Fk-1* Fk-1 using Apriori 5: for each itemset ck Ck do
6: Sup(Union(ck)=Union_Intervals(ck)
7: Gather the sizes of all ck’s sub-intersection terms
8: Compute sup(ck) using (1)
9: if sup(ck)>=minsup then 10: Fk=Fkck
11: end
12: F=FFk
13.end
Hình 2.16 Thuật toán PIETM
Procedure Union_Intervals Input:
Output:
1: Let A, B be the two itemsets in Fk-1 from which ck is generated 2: Union all the intervals in A.L and B.L as L(Union(ck))
3: Merge these intervals if they are mergeable (i.e., if the intervlas are contiguous)
4: Return Num(L(Union(ck)))
Hình 2.17 Hàm Union_Intervals
Ví dụ 2.16: Cho một CSDL giao tác gồm 8 giáo tác 17 hạng mục
Nội dung | Nội dung sắp xếp với minsup =2 | |
1 | a, b, c, e | a, b, c |
2 | a, c, f, g | a, c |
3 | b, d, h | b, d |
4 | a, c, i, j, k | a, c |
5 | a, b, l | a, b |
6 | a, c, m, n | a, c |
7 | b, c, p | b, c |
8 | a, b, c, d, q, r | a, b, c, d |
Có thể bạn quan tâm!
-
Phương Pháp Khai Thác Theo Chiều Ngang Để Trích Xuất Các Tập Phổ Biến -
Một Số Thuật Toán Khai Thác Tập Phổ Biến -
Phương pháp khai thác theo chiều ngang để trích xuất các tập phổ biến - 5 -
Phương Pháp Tìm Kiếm Theo Chiều Rộng Và Theo Chiều Sâu -
Biểu Diễn Tập Dữ Liệu Trên Ma Trận Bit -
Phương pháp khai thác theo chiều ngang để trích xuất các tập phổ biến - 9
Xem toàn bộ 84 trang tài liệu này.
Bảng 2.13 CSDL giao tác gồm 8 giáo tác và 17 hạng mục
Bước 1: Xây dựng cây FP-Tree
Root
a: 6
[1-6]
b: 2
[7-8]
b: 3
[1-3]
c: 3
[4-6]
c: 1
[7-7]
d: 1
[8-8]
c: 2
[1-2]
d: 1
[1-1]
Hình 2.18 Ví dụ xây dựng cây FP-Tree và các khoảng giao tác
Cho X biểu thị một nút trong cây giao tác và y biểu thị số lượng giao tác trong đó có xuất hiện X. Một khoảng [s, e] được liên kết với X. Trong [s, e], s chỉ ra số giao tác (id) bắt đầu được gắn nhãn và e cho biết (id) kết thúc cũng được gắn nhãn, trong đó y = (e - s + 1). Giả sử rằng X có k nút con, và mỗi nút con có giao tác yi, trong đó 1 ≤ i ≤ k. Khoảng K trong con của X được liên kết với [s1, e1], [s2, e2], ..., [sk, ek]. Mỗi khoảng giao tác được xây dựng theo bốn trường hợp sau:
s1 = s (2)
e1 = s1 + y1- 1 (3)
si = ei - 1 + 1, for i = 2,3,.....k (4)
ei = si + yi - 1, for i = 2,3,...,k (5)
Ví dụ, trong hình 2.18, nút gốc có hai con. Ban đầu, giao tác (id) bắt đầu được gắn nhãn s là 1 trong thư mục gốc.
Đối với nút a, s1 = 1, e1 = 1 + 6 - 1 = 6. Do đó a có khoảng [s1-e1]=[1-6]
Đối với nút b, s2 = e1 + 1 = 7, e2 = s2 + 2 - 1 = 8. b có khoảng [s2-e2]=[7-8] Tương tự, đối với nút mức 1
Nút b là con của a, khoảng b, s1 = 1, e1 = 1 + 3 - 1 = 3, là [1-3].
Nút c là con của a, khoảng của c, s2 = e1 + 1 = 4, e2 = s2 + 3 – 1 = 6, là [4-6]. Nút c là con của b, khoảng của c, s3 = e2 + 1 = 7, e3 = s3 + 1 – 1 = 7, là [7-7]. Nút d là con của b, khoảng của d, s4 = e3 + 1 = 8, e4 = s3 + 1 – 1 = 8, là [8-8].
Tương tự, đối với nút mức 2
Nút c là con b, khoảng c, s1 = 1, e1 = 1 + 2 - 1 = 2, là [1-2].
Tương tự, đối với nút mức 3
Nút d là con c, khoảng d, s1 = 1, e1 = 1 + 1 - 1 = 2, là [1-1].
Khoảng giao tác | |
a | [1-6] |
b | [1-3],[7-8] |
c | [1-2],[4-6],[7-7] |
d | [1-1],[8-8] |
Bảng 2.14 Danh sách các khoảng giao tác
Một danh sách khoảng giao tác cho mục n có thể được tạo bằng cách thu thập tất cả các khoảng liên kết với mục n trong cây giao tác. Bảng 2.13 cho thấy danh sách khoảng giao tác trong hình 2.18.
Bước 2: Đếm các hạng mục với nguyên lý Bao gồm-Loại trừ
Lập danh sách khoảng giao tác của Union(ck) bằng cách sáp nhập các danh sách khoảng giao tác. Quá trình kết hợp các danh sách khoảng giao tác như sau: L(Z) là danh sách được xây dựng sau khi hợp nhất các danh sách khoảng giao tác của hai tập X và Y, trong đó X = Union (a1,a2 ... ak-2,ak-1), Y = ak và Z = Union (a1,a2 ... ak-2,ak-1, ak). Num(L(Z)) biểu thị tổng số giao tác trong L(Z). Để khoảng I1 = [sx, ey] bao gồm trong X và khoảng I2 = [sy, ey] được đưa vào trong Y. Hai trường hợp phải được xem xét khi chúng được hợp nhất:
Trường hợp 1: I1 chứa I2 hoặc I1 được chứa trong I2. Trường hợp 2: I1 I2 =
Khoảng giao tác | |
L(Union(ab)) = {[1, 6], [7,8]} | L(Union(bc)) = {[1, 3], [4, 6], [7,8]} |
L(Union(ac)) = {[1, 6], [7,7]} | L(Union(bd)) = {[1, 3], [7,8]} |
L(Union(ad)) = {[1, 6], [8, 8]} | L(Union(cd)) = {[1, 2], [4,6], [7,7], [8, 8]} |
Hạng mục
Bảng 2.15 Kết hợp các khoảng giao tác Trong trường hợp 1: I1 được thêm vào L(Z) nếu I1 chứa I2.
Trong trường hợp 2: I1 và I2 được thêm vào L(Z) cùng một lúc. Ví dụ, chúng
ta hợp nhất các danh sách khoảng giao tác trong các mục a và b trong bảng 2.13. Trường hợp 1 tồn tại trong khoảng [1,6] trong a và khoảng [1,3] trong b, do đó khoảng [1,6] sẽ được thêm vào L(Union(ab)). Trường hợp 2 tồn tại trong khoảng [1,6] và trong khoảng còn lại [7,8] trong b. Cuối cùng, vì [1,6] và [7,8] có tám giao tác trong L(Union (ab)), Num (L(Union (ab))) =8. Bảng 2.14 bao gồm các kết quả của tất cả các danh sách khoảng giao tác của các tập mục trong bảng 2.13. Một mục ứng viên ck có thể được tính bằng (1) sau khi xác định Num(L(Union (ck) )).
Ví dụ, tính độ phổ biến của 2 hạng mục bằng cách sử dụng (1) và thông tin trong bảng 2.15. Cho phép tính sup(AB) và sup(BD) từ bảng 2.13:
sup(ab) = |a b| = |a| + |b| - |ab|
= sup(a) + sup(b) - Num(L(Union(ab)))
= 6 + 5 - 8 = 3
sup (BD) = |bd| = |b| + |d| - |bd|
= sup(b) + sup(d) - Num(L(Union(bd)))
= 5 + 2 - 5 = 2.
Ta thấy trong bảng 2.13, ab xuất hiện trong bốn giao tác, tid = {1, 5, 8} và bd trong hai giao tác, tid = {3, 8}. Do đó, ab và bd được tính bằng (1)
Bảng ví dụ về khai thác các tập phổ biến bằng cách sử dụng PIETM
Ck | k-Union | Độ phổ biến k-itemset | Fk | |
2 | ab | Num(L(Union(ab)))=8 | Sup(ab)=sup(a)+sup(b)-8 =6+5-8=3 | ab |
ac | Num(L(Union(ac)))=7 | Sup(ac)=sup(a)+sup(c)-7 =6+6-7=5 | ac | |
ad | Num(L(Union(ad)))=7 | Sup(ad)=sup(A)+sup(d)-7 =6+2-7=1 | ||
bc | Num(L(Union(bc)))=8 | Sup(bc)=sup(B)+sup(c)-8 =5+6-8=3 | bc | |
bd | Num(L(Union(bd)))=5 | Sup(bd)=sup(b)+sup(d)-5 =5+2-5=2 | bd | |
cd | Num(L(Union(cd)))=7 | Sup(cd)=sup(c)+sup(d)-7 =6+2-7=1 | ||
3 | abc | Num(L(Union(abc)))=8 | Sup(abc)=8- (sup(a)+sup(b)+sup(c))+sup(ab)+sup(ac)+ sup(bc)=8-(6+5+6)+(3+5+3)=2 | abc |
bcd | Num(L(Union(bcd)))=8 | Sup(bcb)=8- (sup(b)+sup(c)+sup(d))+sup(bc)+sup(bd)+ sup(cd)=8-(5+6+2)+(3+2+1)=1 |
Bảng 2.16 Khai thác tập phổ biến bằng PIETM
Nhận xét:
Ưu điểm: Lợi thế của PIETM bao gồm là sự đơn giản của Apriori và hiệu quả của của cây FP-Tree. PIETM sử dụng một cấu trúc hiệu quả, được gọi là danh sách khoảng thời giao tác, để dễ cho việc tính toán.
Hạn chế: là không tính độ phổ biến của hạng mục trực tiếp. Thay vào đó, PIETM sử dụng Nguyên tắc toán học của Bao gồm – Loại trừ để tính toán độ phổ biến của các hạng mục. Do đó việc xây dựng các danh sách khoảng giao tác có thể dẫn đến PIETM có thời gian thực hiện lâu hơn.